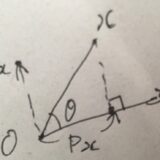「線形代数学」の記事一覧
対称行列のスペクトル分解とは:具体例、証明
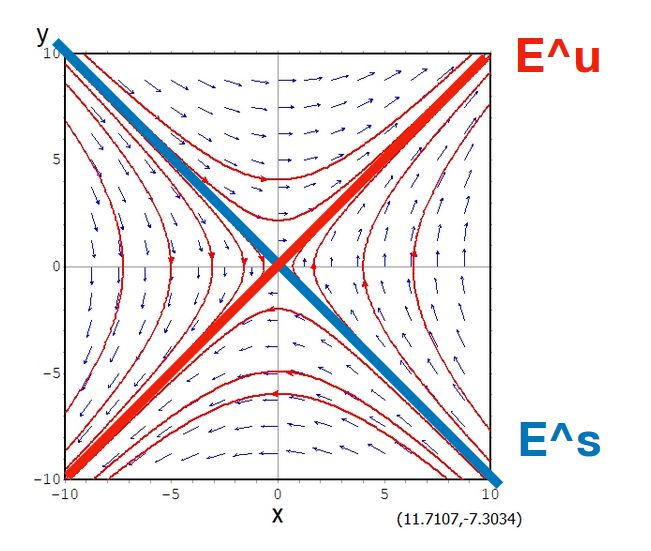
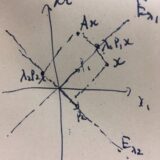
不変部分空間とは:固有空間、射影行列を例に
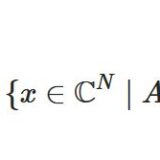
固有空間の求め方、代数的・幾何学的重複度とは:部分空間となることの証明
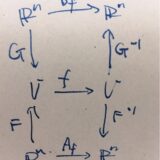
線形写像のランク、行列式、固有値は表現行列によらず定まることの証明
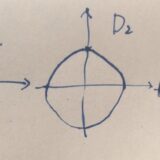
pノルムとは:絶対値ノルム、最大値ノルム、同値なノルム
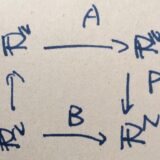
行列の相似とは:対角化との関係、不変量(ランク、行列式、固有値)
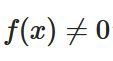
連続関数はゼロでない点の近傍でゼロでないことの証明
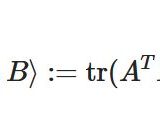
行列のフロベニウス内積とは、性質:回転行列のなす角度を例に
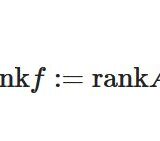
線形写像の単射・全射・全単射の判定:ランクによる求め方
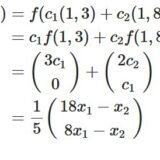
線形写像の求め方:基底の行き先で一意に決まる
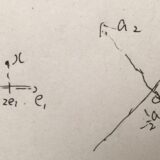
線形写像の表現行列、基底の変換の求め方を解説
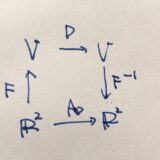
線形写像、表現行列をなぜ学ぶか:同型写像の考え方

線形代数における座標・成分・基底とは何か
直交多項式とは:ルジャンドル多項式、微分方程式を例に
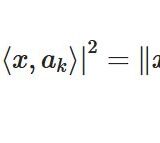
ベッセルの不等式・パーセバルの等式とは:有限のケースで証明
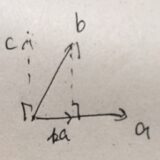
コーシー・シュワルツの不等式とは:証明と幾何学的な意味
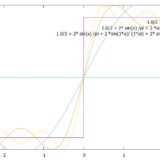
三角関数の直交性とは:フーリエ級数展開と関数空間の内積
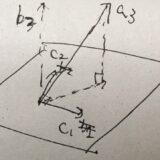
シュミットの直交化法とは:正規直交基底の具体的な求め方