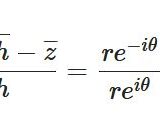
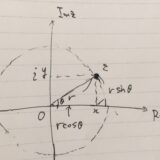
オイラーの公式、極形式、ド・モアブルの定理とは:複素指数関数、三角関数の性質
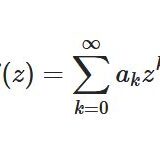
複素べき級数、収束半径とは:指数・三角関数を例に
関数列の収束:各点収束、一様収束、L^p収束とは
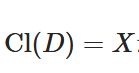
稠密性とは:有理数、ワイエルシュトラスの近似定理を例に
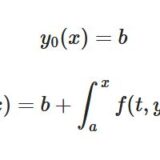
完備性とは:無理数、微分方程式の解の近似を例に
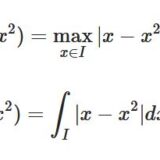
距離空間とは:関数空間、ノルム、内積を例に
平方剰余の相互法則とは 例と証明
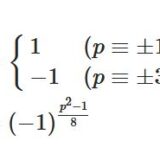
ガウスの補題、平方剰余の第二補充法則を解説
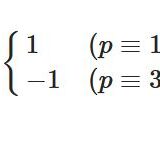
ルジャンドル記号の性質、平方剰余の第一補充法則を解説
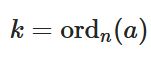
整数の位数、原始根とその性質 オイラーの判定条件への応用
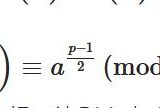
平方剰余、オイラーの判定条件、ルジャンドル記号とは何か
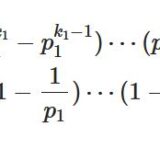
オイラーのファイ関数の性質、計算方法
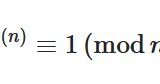
数論におけるオイラーの定理、ファイ関数とは?
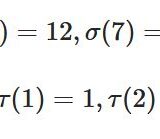
数論的関数、乗法的関数とは何か:約数関数を例に
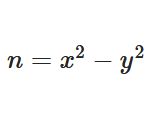
素因数分解のフェルマー法とは何か
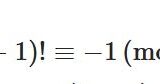
ウィルソンの定理とは? 具体例、証明を紹介
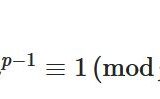
フェルマーの小定理、フェルマーテスト、擬素数とは何か
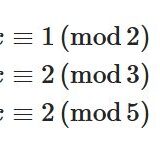
線形合同式の解き方、中国式剰余定理とは何か

