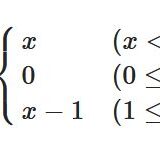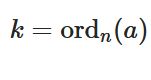平方剰余、オイラーの判定条件、ルジャンドル記号とは何か

どうも、木村（@kimu3_slime）です。

今回は、数論における平方剰余、オイラーの判定条件、ルジャンドル記号について紹介します。

平方剰余とは
オイラーの基準とルジャンドル記号
こちらもおすすめ

平方剰余とは

\(ax\equiv b \,(\mathrm{mod} n)\)という形の合同式は、線形合同式（1次合同式）と呼ばれ、その解ける条件、解き方は知られています。特に\(a,n\)が互いに素のときは、\(n\)を法としてただひとつの解を持ちます。

さてこれを発展させた問題、\(ax^2+bx+c\equiv 0 \,(\mathrm{mod}\, n)\)という2次の合同式は、どうやったら解けるのでしょうか？

その特殊なケースとして、1次の項がないケース\(x^2 \equiv a \,(\mathrm{mod} \,n)\)は、どうやって解けるのでしょうか。その鍵は、平方剰余と呼ばれる概念と、平方剰余の相互法則と呼ばれる定理です。

\(a\)を整数、\(n\)を正の整数で、\(a,n\)を互いに素とします。\(x^2 \equiv a \,(\mathrm{mod} \,n)\)が解を持つ時、\(a\)は\(n\)を法とする平方剰余である（quadratic residue of \(n\)）、と呼びます。平方剰余でないときは、平方非剰余（quadratic nonresidue of \(n\)）と呼びます。

整数の二乗によって表される数\(x^2\)を平方数と呼び、ある平方数のあまりになっている数を平方剰余と呼んでいるわけです。

前提として、\(a,n\)を互いに素とするという仮定があります。この仮定を外して、\(a=0\)を考えれば、\(x^2 \equiv 0 \,(\mathrm{mod} \,p)\)は\(p\)がなんであろうが、\(x= 0\)という（自明な）解をいつでも持ちますね。法\(n\)に関係のない性質なので、\(0\)は平方剰余の議論からあらかじめ外しておくわけです。

簡単なケースとして、\(n\)が素数\(p\)のケースを調べていきましょう。

\(p=2\)のとき、\(a= 1\)を考えます。\(x^2 \equiv 1 \,(\mathrm{mod} \,2)\)は\(x\equiv 1\)という解を持つので、\(1\)は\(2\)を法とする平方剰余です。これも明らかなケースなので、\(p\)を奇数である素数、\(3\)以上の素数、奇素数と仮定することが多いです。

\(p=3\)はどうでしょうか。\(a=1,2\)について考えます。\(x^2 \equiv 1 \,(\mathrm{mod} \,3)\)は\(x\equiv 1\)という解を持つので、\(1\)は\(3\)を法とする平方剰余です。\(2^2 \equiv 1 \,(\mathrm{mod} \,3)\)なので、\(x^2 \equiv 2 \,(\mathrm{mod} \,3)\)の解は存在しません。よって、\(2\)は\(3\)を法とする平方非剰余です。（フェルマーの小定理によれば、\(x,p\)が互いに素、\(p=3\)のとき、\(x^2 \equiv 1 \,(\mathrm{mod}\, 3)\)です。平方数の剰余が必ず1となるので、\(2\)は平方剰余ではありません）

\(p=5\)について考えます。\(1^2 \equiv 1\)、\(2^2 \equiv 4\)、\(3^2 \equiv 4\)、\(4^2 \equiv 1\)なので、\(1,4\)が\(5\)を法とする平方剰余で、\(2,3\)が\(5\)を法とする平方非剰余です。この例を見ると、平方剰余な数の平方は\(1\)に合同で、非平方剰余の平方は\(p-1=4\)に合同ですね。

\(p=7\)について考えます。\(1^2 \equiv 1\)、\(2^2 \equiv 4\)、\(3^2 \equiv 2\)、\(4^2 \equiv 2\)、\(5^2\equiv 4\)、\(6^2 \equiv 1\)です。よって、\(1,2,4\)が\(7\)を法とする平方剰余で、\(3,5,6\)が\(7\)を法とする平方非剰余です。

今回はどんな性質があるでしょうか。2乗ではうまい性質が見いだせませんが、3乗なら良い性質があるのがわかります。平方剰余数の3乗を調べると、\(1^3 \equiv 1\)、\(2^3 \equiv 1\)、\(4^3 \equiv 2^6 \equiv 2^3 \equiv 1\)です。非平方剰余数の3乗を調べると、\(3^3\equiv2\cdot 3\equiv 6\)、\(5^3 \equiv 4\cdot 5 \equiv 6\)、\(6^3 \equiv 1\cdot 6 \equiv 6\)と\(p-1\)に等しいですね。

オイラーの基準とルジャンドル記号

さて、今までの話を一般化したものが、オイラーの判定条件、オイラーの基準（Euler’s criterion）です。

\(a\)は整数、\(p\)は奇素数で、\(a,p\)が互いに素であるとする。

このとき、\(a\)が\(p\)を法とする平方剰余であることは、\(a^{\frac{p-1}{2}} \equiv 1\,(\mathrm{mod} \,p)\)と同値。

（\(a\)が\(p\)を法とする非平方剰余であることは、\(a^{\frac{p-1}{2}} \equiv -1 \,(\mathrm{mod} \,p)\)と同値。）

オイラーの基準の証明を、一部紹介しましょう。

まず、\(a\)が\(p\)を法とする平方剰余であると仮定し、\(x\)を\(x^2 \equiv a \,(\mathrm{mod} \,p)\)を満たすものとします。

このとき、\(x,p\)は互いに素です。仮に互いに素でないとすると、\(2\)以上の公約数\(d\)を持ちます。そして、\(a=x^2+kp\)を満たす整数\(k\)があります。\(d\)は\(x^2\)の約数でもあるので、\(d\)は\(a\)の約数ともなります。これは\(a,p\)が互いに素であることに矛盾します。

したがって、フェルマーの小定理が適用でき、\(x^{p-1} \equiv 1\,(\mathrm{mod} \,p)\)です。よって、\(a^{\frac{p-1}{2}} \equiv (x^2)^{\frac{p-1}{2}} \equiv 1\,(\mathrm{mod} \,p)\)が得られました。

これの逆を示すには、整数の位数や原始根と呼ばれる考え方が必要となります。

参照：整数の位数、原始根とその性質オイラーの判定条件への応用

「\(a\)が\(p\)を法とする非平方剰余であることは、\(a^{\frac{p-1}{2}} \equiv -1 \,(\mathrm{mod} \,p)\)と同値」は、前半の主張から導かれるものです。\(a,p\)は互いに素であることから、フェルマーの小定理により\(a^{p-1}-1\equiv 0 \,(\mathrm{mod} \,p)\)です。これを因数分解すると、\((a^{\frac{p-1}{2}}-1)(a^{\frac{p-1}{2}}+1)\equiv 0 \,(\mathrm{mod} \,p)\)です。\(a^{\frac{p-1}{2}}-1,a^{\frac{p-1}{2}}+1\)の両方が0に合同であると仮定すると、\(1\equiv -1\)ですが、\(p\)が\(2\)でない素数の時これはありえません。したがって、\(a^{\frac{p-1}{2}}-1,a^{\frac{p-1}{2}}+1\)のどちらか一方だけが0に合同になります（\(p\)が素数のとき、零因子が存在しない）。前半の主張より、\(a\)が平方非剰余のときに\(a^{\frac{p-1}{2}}-1 \equiv 0\)はありえないので、\(a^{\frac{p-1}{2}} \equiv -1 \,(\mathrm{mod} \,p)\)との同値性が導かれます。

平方剰余の性質や、オイラーの判定条件を言い換えるために、次の記法はよく使われます。\(a\)を整数、\(p\)を奇素数で、\(a,p\)を互いに素とします。

\[ \begin{aligned}\left(\frac{a}{p}\right)= \begin{cases}1 & (aがpを法とする平方剰余のとき )\\-1 & (aがpを法とする平方非剰余のとき)\end{cases}\end{aligned} \]

この記号\(\left(\frac{a}{p}\right)\)をルジャンドル記号（Legendre symbol）と呼びます。分数と似た性質を持つので、分数に似た表記をしていますが、分数とは当然別物なので注意しましょう。\(a\)をルジャンドル記号の分子（numerator）、\(p\)を分母（denominator）と呼びます。

「\(1,4\)が\(5\)を法とする平方剰余で、\(2,3\)が\(5\)を法とする平方非剰余」という事実は、ルジャンドル記号を使って言い換えれば、\(\left(\frac{1}{5}\right)=\left(\frac{4}{5}\right)=1\)、\(\left(\frac{2}{5}\right)=\left(\frac{3}{5}\right)=-1\)と表せます。

ルジャンドル記号を用いれば、オイラーの基準は\(\left(\frac{a}{p}\right) \equiv a^{\frac{p-1}{2}} \,(\mathrm{mod} \,p)\)とひとつの数式で表せます。この記法は計算が便利であり、平方剰余の相互法則を表すために使われるものです。別記事で紹介予定。

以上、平方剰余、オイラーの判定条件、ルジャンドル記号を例を通じて紹介しました。

\(p\)が大きくなってくると、オイラーの判定条件を適用するのは現実的ではありませんが、それでも平方剰余の理論的な言い換えとしてシンプルなものです。

平方剰余の相互法則を理解するにあたって、まずは小さな素数での平方剰余の性質、オイラーの判定条件から学んでいくと良いと思います。

木村すらいむ（@kimu3_slime）でした。ではでは。