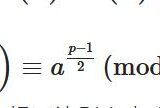整数の位数、原始根とその性質オイラーの判定条件への応用

どうも、木村（@kimu3_slime）です。

今回は、整数の位数、原始根とはどういうものか、そのオイラーの判定条件への応用を紹介します。

整数の位数、原始根とは
位数、原始根の性質
オイラーの判定条件への応用
こちらもおすすめ

整数の位数、原始根とは

今回の議論の出発点となるのは、数論におけるオイラーの定理\(a^{\phi(n)} \equiv 1 \,(\mathrm{mod}\, n)\)です。\(\phi(n)\)は\(n\)と互いに素な\(1\)以上\(n\)以下の数の個数を表すもので、オイラーの\(\phi\)関数と呼ばれています。

（\(n\)と互いに素な）どんな整数\(a\)も、べき乗していくと必ず\(1\)に合同になる、という性質があるわけです。実際には、\(\phi(n)\)乗で\(1\)に合同になることもあれば、それ以下のべきで\(1\)に合同になることもあります。単純な例ですが、\(a=1\)とすれば、\(\phi(n)\)が大きな値であろうが、\(a^1\equiv 1 \,(\mathrm{mod}\, n)\)です。

\(a\)を整数、\(n\)を2以上の整数で、\(a,n\)は互いに素とします。このとき、\(a^k \equiv 1 \,(\mathrm{mod}\, n)\)を満たす最小の正の整数\(k\)を、\(n\)を法とする\(a\)の位数（order of \(a\) modulo \(n\)）と呼びます。これを\(k= \mathrm{ord}_n(a)\)と書くことがあります。

また、\(a\)の位数が\(\phi (n)\)であるとき、\(a\)を整数\(n\)の原始根（primitive root of \(n\)）と呼びます。

例えば、\(n=3\)としましょう。互いに素な数は\(1,2\)で、\(\phi(2)=2\)です。\(a=1\)の位数は\(1\)なので、\(1\)は\(3\)の原始根ではありません。\(a=2\)の位数を考えると、\(a^1\not \equiv 1\)で、\(a^{\phi(2)} \equiv 1\)なので、\(2\)は\(3\)の原始根です。\(n=4\)も同様の状況が起こります。

\(n=5\)のとき、\(n\)と互いに素なのは\(1,2,3,4\)の\(\phi(5)=4\)個です。\(1\)の位数は\(1\)です。\(2,4,8 \not \equiv 1\)なので、\(2\)の位数は\(4\)で、\(2\)は原始根です。\(3,9,27 \not \equiv 1\)なので、\(3\)は原始根です。\(4^2 \equiv 1 \)なので、\(4\)の位数は\(2\)です。

オイラーの定理\(a^{\phi(n)} \equiv 1 \,(\mathrm{mod}\, n)\)より、位数は必ず\(\phi(n)\)以下となります。そして、小さな数からべき乗していくと\(\phi(n)\)乗でしか\(1\)にならないとき、その数を原始根と呼んでいるわけです。

位数の定義では、互いに素でない数を除外しています。例えば\(n=4\)のとき、\(a=0,2\)は何乗かすると\(1\)に合同にならないまま、\(0\)に合同になります。線形合同式\(ax \equiv 1\,(\mathrm{mod}\, n )\)は、\(a,n\)が互いに素なときのみ解を持ち、そうでないときに解を持たないことが知られています。互いに素でないときに\(a^k\equiv 1\)を満たすとすると、\(x=a^{k-1}\)という線形合同式が解を持つことになり、矛盾を起こします。だから、位数を考えるときは互いに素でない数は考えなくて良い、というわけです。

位数、原始根の性質

位数については、次の性質が知られています。

整数\(a\)の\(n\)を法とする位数を\(k\)とする。\(\ell\)を任意の正の整数とする。このとき、\(a^{\ell} \equiv 1 \,(\mathrm{mod}\, n)\)と\(k \mid \ell\)は同値。

特に、オイラーの定理より\(\ell =\phi(n)\)のときを考えれば、\(k \mid \phi(n)\)である。

べき乗して\(1\)に合同になるときは、そのべき\(\ell\)は\(k\)の倍数である、\(k\)は\(\ell\)を割り切ることと同値、というわけです。\(n=5\)の例では、\(4\)の位数は\(2\)で、\(\phi(5)=4\)の約数となっていました。確かに、そういうことしかありえなそうな気がします。

証明してみましょう。

\(a^{\ell} \equiv 1 \,(\mathrm{mod}\, n)\)と仮定します。\(\ell\)を\(k\)で割ると、除法の原理より\(\ell =qk+r\)、\(0\leq r <k\)と表せます。\(a^{\ell}=a^{qk+r}=(a^k)^q a^r\)なので、\(a\)の位数が\(k\)であること、\(a^{\ell}\equiv 1\cdot a^r\)です。仮定と合わせれば、\(a^r \equiv 1\)です。ここで\(r\geq 1\)とすると、\(r<k\)なので、\(a\)の位数が\(k\)であること（\(1\)に合同になる最小のべきであること）に反するので、\(r=0\)しかありえません。すなわち、\(k \mid \ell\)が示せました。

逆に、\(k \mid \ell\)、\(\ell = mk\)となる整数\(m\)が存在するとしましょう。\(a\)の位数が\(k\)であること、合同式の性質から、\((a^k)^m \equiv 1^m\)です。すなわち、\(a^{\ell} \equiv 1 \,(\mathrm{mod}\, n)\)が得られました。

原始根の基本的な性質は、べき乗していくと（互いに素な）すべての値を取る（巡回・生成する）ということです。

\(n=5\)のとき、\(2\)は原始根で、\(2,4,8 \equiv 3,16 \equiv 1\)です。\(3\)は原始根で、\(3,9\equiv 4,27 \equiv 2 ,81 \equiv 1\)です。これは一般化されます。

\(r\)を素数\(p\)の原始根とすると、\(r,r^2,\dots,r^{p-1}\)は\(1,2,\dots,p-1\)のいずれかに\(p\)を法として合同です。

まず、\(r,r^2,\dots,r^{p-1}\)は\(p\)を法として互いに合同ではありません。\(r^{i} \equiv r^{j}\)と仮定すると、法\(p\)が素数であることから、合同式の性質より\(r\)で割ることができ、\(1 \equiv r^{j-i}\)が得られます。\(i\neq j\)とすると、\(r\)が原始根であること（位数\(p-1\)であること）に矛盾します。

原始根は\(0\)でなく、\(p-1\)個の整数\(r,r^2,\dots,r^{p-1}\)が互いに合同でないので、それらは\(1,2,\dots,p-1\)のいずれかに\(p\)を法として合同であることがわかります。これはもう少し一般に同様の議論ができます。

\(a\)の位数を\(k\)とする。\(a,a^2,\dots,a^k\)は\(n\)を法として互いに合同ではない。

\(n\)と互いに素な正の整数を\(a_1,a_2,\dots,a_{\phi(n)}\)とする。\(a\)が\(n\)の原始根ならば、\(a,a^2,\dots,a^k\)は\(a_1,a_2,\dots,a_{\phi(n)}\)のいずれかに合同。

さて、そんな原始根というものはいつでも存在するのでしょうか？　素数\(p\)については、原始根が必ず存在することが知られています。

\(p\)を素数で、正の整数\(d\)を\(d \mid p-1\)を満たすものとする。このとき、\(p\)を法として位数\(d\)である互いに合同でない整数は\(\phi(d)\)個存在する。

特に、\(p\)の原始根はいつでも存在する。そして、\(\phi(p-1)\)個の相互に合同でない原始根が存在する。

前半から後半を導くことは簡単です。\(d=p-1\)とすると、\(d \mid p-1\)を満たすので、\(p\)を法として位数\(p-1\)である互いに合同でない整数は\(\phi(p-1)\)個存在することになります。オイラーの\(\phi\)関数は、素数\(p\)に対して\(\phi(p)=p-1\)なので、位数が\(p-1\)の整数たちは原始根であるとわかりました。

前半の主張の証明は、簡単ではありません。「\(x^{d}-1 \equiv 0 \,(\mathrm{mod}\, p)\)はちょうど\(d\)個の解をもつ」という結果を含む、数論におけるラグランジュの定理から示せます。証明は、例えば「Elementary Number Theory」8章を参照してください。

オイラーの判定条件への応用

位数、原始根の考え方を、オイラーの判定条件に応用してみましょう。

\(a\)は整数、\(p\)は奇素数で、\(a,p\)が互いに素であるとする。

このとき、\(a\)が\(p\)を法とする平方剰余であることは、\(a^{\frac{p-1}{2}} \equiv 1\,(\mathrm{mod} \,p)\)と同値。

確認しておくと、\(a\)が\(p\)を法とする平方剰余であるとは、\(x^2 \equiv a \,(\mathrm{mod} \,p)\)が解を持つことです。「\(a\)が\(p\)を法とする平方剰余である」ならば「\(a^{\frac{p-1}{2}} \equiv 1\,(\mathrm{mod} \,p)\)」は既に示しました。

逆を示しましょう。\(a^{\frac{p-1}{2}} \equiv 1\,(\mathrm{mod} \,p)\)を仮定して、\(a\)を平方のあまりとして表せないか考えます。

\(p\)は素数なので、その原始根が存在します。そのひとつを\(r\)としましょう。\(r,r^2,\dots,r^{p-1}\)は\(1,2,\dots,p-1\)のいずれかに\(p\)を法として合同なので、\(r^k \equiv a\)を満たす整数\(k\)、\(1\leq k \leq p-1\)が存在します。仮定と合同式の性質を用いれば、\(1 \equiv a^{\frac{p-1}{2}} \equiv r^{\frac{k(p-1)}{2}} \)です。

この合同式を満たす時、指数\(\frac{k(p-1)}{2}\)は\(r\)の位数\(p-1\)の倍数でなければならない、という位数の性質がありました。つまり、\(\frac{k}{2}\)は整数であり、\(k\)は偶数です。そこで\(k=2\ell \)、\(x=r^{\ell}\)とします。\(x^2 =r^{2\ell} \equiv a\)です。よって、\(a\)は\(p\)を法とする平方剰余であることがわかりました。

構成するステップをまとめれば、適当な原始根\(r\)を見つけ、\(r^k \equiv a\)を満たす整数\(k\)が必ず偶数として見つかるので、その半分\(\ell\)により\(x=r^{\ell}\)とすれば良いわけですね。

例えば\(p=11\)ならば、原始根として\(r=2\)が選べます。例えば\(a=5\)は\(p\)と互いに素で、\(a^{\frac{11-1}{2}} \equiv 5\cdot 3\cdot 3 \equiv 1\,(\mathrm{mod} \,p)\)を満たします。\(r^4 =16 \equiv a\)と\(k=4\)で表せるので、\(x=r^2=4\)とします。そうすれば、\(4^2\equiv a\)と、平方剰余として\(a\)が表せます。原始根はべき乗していけばどんな値も取る、\(a\)も表せるというのが便利です。

以上、整数の位数、原始根とはどういうものか、その性質と、オイラーの判定条件への応用を紹介しました。

今回考えたのは整数ですが、抽象代数学、群論にも要素の位数という考え方が定義されます。位数がオイラー関数を割り切る\(k \mid \phi(n)\)性質は、群論におけるラグランジュの定理として一般化されるものです。

平方剰余に関する話題や、整数のべき乗のあまりを考えるときに、位数や原始根は役立つので、ぜひ馴染んでみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。