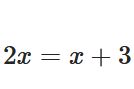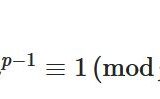どうも、木村(@kimu3_slime)です。
今回は、線形合同式とは何か、その解き方、中国式剰余定理について解説します。
線形合同式とは、解き方
\(5\)本の束になった鉛筆が\(x\)束あった(\(x\)は整数)。それをばらし、1ダース(12本)を基準として数えると、あまりが\(1\)本となった。このとき、\(x\)は何本でありうるか?
この問題は\(5x \equiv 1 \,(\mathrm{mod}\, 12 )\)という合同式を満たす\(x\)を見つける問題です。一般に、\(ax\equiv b \,(\mathrm{mod}\, n )\)という形の方程式は、線形合同式(linear congruence)、合同方程式、1次合同式と呼ばれます。
\(5x \equiv 1 \,(\mathrm{mod}\, 12 )\)を解いてみましょう。このくらいの問題なら、あたりをつけて解けますね。
5の倍数\(5,10,15,20,25,\dots\)を12で割ったあまりが1になるのは何か。\(25\)は良さそうな数ですね。\(25= 2\cdot 12+1\)なので、\(x=5\)はひとつの解です。
\(k\)を整数として、\(x=5+12k\)について考えると、\(5x =(2+5k)\cdot 12 +1\)です。したがって、\(x \equiv 5 \,(\mathrm{mod}\, 12 )\)が解となります。
\(x \not \equiv 5 \,(\mathrm{mod}\, 12 )\)のときは、解ではありません。\(x=5+12k+r\)、\(1\leq r \leq 11\)とします。\(5x =(2+5k+\frac{5r}{12})\cdot 12 +1\)となりますが、\(5,12\)は互いに素なので、\(\frac{5r}{12}\)は整数とならず、したがって\(5r\)は\(12\)の倍数となりません。よって、\(5x \not \equiv 1 \,(\mathrm{mod}\, 12 )\)が導かれます。
以上をまとめれば、\(x \equiv 5 \,(\mathrm{mod}\, 12 )\)を満たす整数\(x\)が、\(5x \equiv 1 \,(\mathrm{mod}\, 12 )\)のすべての解です。
線形合同式は、いつでも合同をのぞいてただひとつの解を持つわけではありません。
例えば、\(2x\equiv 0 \,(\mathrm{mod}\, 12 )\)を考えます。\(x\equiv 0\,(\mathrm{mod}\, 12 )\)と\(x\equiv 6\,(\mathrm{mod}\, 12 )\)はどちらも解です。しかし、相互に合同ではありません\(0 \not \equiv 6\,(\mathrm{mod}\, 12 )\)。
また、\(2x\equiv 1 \,(\mathrm{mod}\, 12 )\)には解が存在しません。\(2x-1\)は常に奇数であり、\(12\)の倍数(偶数)とはなりえないからです。
線形合同式の解の存在については、次のことが知られています。
\(a,b,n\)を整数とし、\(d= \mathrm{gcd}(a,n)\)とする。線形合同式\(ax\equiv b \,(\mathrm{mod}\, n )\)が解を持つことは、\(d \mid b\)と同値。
解を持つときは、\(n\)を法として\(d\)個の相互に合同でない解を持つ。
特に、\(d=1\)のとき、線形合同式は合同を除いてただひとつの解をもつ。
\(ax\equiv b \,(\mathrm{mod}\, n )\)は、\(ax-nk=b\)という\(x,k\)に関する1次不定方程式と同値なので、1次不定方程式の議論から導けます(解が存在するときは、ユークリッドの互除法により解ける)。証明は「Elementary Number Theory」4章を参照してください。
抽象代数学では、\(ax\equiv 1 \,(\mathrm{mod}\, n )\)という式は、整数の剰余類環\(\mathbb{Z}/n\mathbb{Z}\)における、乗法的逆元(逆数)の定義式です。\(n\)が素数\(p\)のとき、常に乗法の逆元は存在し、\(\mathbb{Z}/p\mathbb{Z}\)は体としての性質を持つことがわかります。
特に、すべての\(x,y\)に対し、\(xy\equiv 0 \,(\mathrm{mod}\, p )\)ならば\(x\equiv 0\)または\(y \equiv 0\)となります(\(xy\equiv 0\)であり、\(x\not \equiv 0\)かつ\(y \not \equiv 0\)を満たす\(x,y\):零因子を持たない。\(\mathbb{Z}/p\mathbb{Z}\)は整域である)。
中国式剰余定理とは
ここまでは単独の線形合同式を考えましたが、いくつかの線形合同式を連立させた問題を考えることもできます。
例えば、次の問題について考えてみましょう。
\[ \begin{aligned} x&\equiv& 1 \,(\mathrm{mod}\, 2 ) \\ x&\equiv& 2 \,(\mathrm{mod}\, 3 ) \\ x&\equiv& 2 \,(\mathrm{mod}\, 5 ) \end{aligned} \]
\(x\equiv 1 \,(\mathrm{mod}\, 2 ) \)より、\(x-1 =2k_1\)と表せます。これを2番目の合同式にあてはめると、\(2k_1+1\equiv 2 \,(\mathrm{mod}\, 3 )\)です。\(2,3\)は互いに素なので、この単独方程式の解は合同を除いて一意であり、\(k_1\equiv 2 \,(\mathrm{mod}\, 3 )\)が解です。
したがって、これらの結果を合わせると、\(x=2k_1+1=2(3k_2+2)+1=6k_2+5\)と表せます。これを3番目の合同式にあてはめると、\(6k_2+5\equiv 2 \,(\mathrm{mod}\, 5 ) \)です。\(6,5\)は互いに素なので、この合同式の解は合同を除いて一意で、\(k_2 \equiv 2 \,(\mathrm{mod}\, 5 ) \)は解です。
よって、\(k_2 =5k_3+2\)と表せます。\(x\)の式に戻せば、\(x=6k_2+5=6(5k_3+2)+5=30k_3+17\)です。以上により、\(x \equiv 17 \,(\mathrm{mod}\,30)\)が解であるとわかりました。
念のためにチェックしてみます。\(x=47\)としましょう。\(2\)で割ったあまりは\(1\)です。\(3\)で割ったあまりは\(2\)です。\(5\)で割ったあまりは\(2\)です。確かに連立合同式を満たしています。さらに、\(47\)に\(30k\)を加えても、\(30\)は\(2,3,5\)を約数としてもつので、それも連立合同式を満たすことがわかりますね。
以上の方法では、合同式を連立させると、考えている法\(n_1=2,n_2=3\)が互いに素ならば、それがひとつの合同式にまとめられる、という議論をしています。\(n_1,n_2\)と\(n_3=5\)も互いに素だったので、さらにひとつの合同式にまとめられて、結果としてすべての合同式を満たす解が見つかるわけです。
この連立合同式の解き方を一般化したものが、中国式剰余定理(Chinese remainder theorem)です。
\(a_1,a_2,\dots,a_r\)を整数、\(n_1,n_2,\dots,n_r\)を互いに素な正の整数とします。このとき、連立合同式
\[ \begin{aligned} x&\equiv& a_a \,(\mathrm{mod}\, n_1 ) \\ x&\equiv& a_2 \,(\mathrm{mod}\, n_2 ) \\ &\vdots& \\ x&\equiv& a_r \,(\mathrm{mod}\, n_r ) \end{aligned} \]
は、\(n_1n_2\cdots n_r\)を法として一意な解を持つ。
証明は「Elementary Number Theory」4章を参照。
中国式剰余定理は、中国の唐の時代に作られたといわれる「孫子算経」によって知られた問題・解法です。「3で割ると2余り、5で割ると3余り、7で割ると2余る数は何か」という問題がのっています。また、日本で言う鶴亀算、キジとウサギの「雉兎同籠」という問題もあったようですね。
中国式剰余定理は、整数\(\mathbb{Z}\)だけでなく、それを一般化した環についても成り立つことが知られています。例えば堀田「代数入門: 群と加群」。
以上、線形合同式とその連立方程式、中国式剰余定理について紹介しました。
形としては合同式ですが、一次不定方程式と同様の議論ができるので、どちらも学んでみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
(2012T)
¥5,437
はじめての数論 原著第3版 発見と証明の大航海‐ピタゴラスの定理から楕円曲線まで
丸善出版 (2014-05-13T00:00:01Z)
¥3,740
裳華房 (1987-09-20T00:00:01Z)
¥3,410