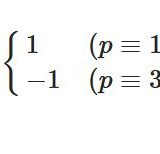どうも、木村(@kimu3_slime)です。
前回は、ルジャンドル記号の性質、平方剰余の第一補充法則を紹介しました。
今回は、数論におけるガウスの補題、平方剰余の第二補充法則を解説します。
ガウスの補題とは
数論におけるガウスの補題(Gauss’s lemma)は、平方剰余の相互法則を示すために使われるものです。
\(a\)を整数、\(p\)を奇素数で、\(a,p\)を互いに素とする。\(a,2a,3a,\dots,\frac{p-1}{2}a\)という数の集まりを考える。そのうち、\(p\)で割ってあまりが\(\frac{p}{2}\)以上の数の個数を\(\ell\)とすると、次の等式が成り立つ。
\[ \begin{aligned}\left(\frac{a}{p}\right) =(-1)^{\ell}\end{aligned} \]
さらに、\(a\)が奇数のときは次の式が成り立つ。
\[ \begin{aligned}\ell \equiv \sum_{k=1}^{\frac{p-1}{2}} \lfloor \frac{ka}{p}\rfloor \,(\mathrm{mod} \,2)\end{aligned} \]
\[ \begin{aligned}\left(\frac{a}{p}\right) =(-1)^{\sum_{k=1}^{\frac{p-1}{2}} \lfloor \frac{ka}{p}\rfloor }\end{aligned} \]
等式の左辺に登場しているのは、ルジャンドル記号です。
\[ \begin{aligned}\left(\frac{a}{p}\right)= \begin{cases}1 & (aがpを法とする平方剰余のとき )\\-1 & (aがpを法とする平方非剰余のとき)\end{cases}\end{aligned} \]
また、\(\lfloor x \rfloor\)は実数\(x\)に対し、\(x\)以下で最大の整数を返す関数で、床関数、ガウス記号、最大整数関数と呼ばれるものです。
まずは、ガウスの補題が何を言っているのか、簡単な具体例で試してみましょう。\(a=1,-1\)のときは平方剰余の第一補充法則で知られているので、他のケースを考えます。
\(p=5\)としましょう。\(a=2\)のとき、\(2,4\)という数を考えます。\(5\)で割ってあまりが\(\frac{5}{2}\)を超えるのは、\(4\)の1個です。ガウスの補題によれば、\(\left(\frac{2}{5}\right) =(-1)^{1}\)です。これは手計算の結果\(\left(\frac{1}{5}\right)=\left(\frac{4}{5}\right)=1\)、\(\left(\frac{2}{5}\right)=\left(\frac{3}{5}\right)=-1\)と一致していますね。\(a=3\)のとき、\(3,6\)を考えます。あまりが\(\frac{5}{2}\)を超えるのは\(3\)のみで、\(\left(\frac{3}{5}\right) =(-1)^{1}\)は正しいです。\(\ell\)の表示式もチェックしてみます。\(a=3\)のとき、\(\lfloor \frac{3}{5}\rfloor+\lfloor \frac{6}{5}\rfloor =1\)で、確かに一致します。
\(p=7\)とします。さきに事実を確認しておくと、\(\left(\frac{1}{7}\right)=\left(\frac{2}{7}\right)=\left(\frac{4}{7}\right)=1\)、\(\left(\frac{3}{7}\right)=\left(\frac{5}{7}\right)=\left(\frac{6}{7}\right)=-1\)です。\(a=2\)については、\(2,4,6\)を考え、あまりが\(\frac{7}{2}\)を超えるのは\(2\)個です。\(a=3\)については、\(3,6,9\)で\(1\)個。\(a=4\)について、\(4,8,12\)で\(2\)個。\(a=5\)のとき、\(5,10,15\)で\(1\)個。ガウスの補題は正しいですね。\(\ell \)の表示式もチェックします。\(a=3\)のとき、\(\lfloor \frac{3}{7}\rfloor+\lfloor \frac{6}{7}\rfloor+ \lfloor \frac{9}{7}\rfloor=1\)です。\(a=5\)のとき、\(\lfloor \frac{5}{7}\rfloor+\lfloor \frac{10}{7}\rfloor+ \lfloor \frac{15}{7}\rfloor=3\)で正しいです。
なぜ、\(a,2a,\dots,\frac{p-1}{2}a\)という数の集まりを考え、\(p\)で割ってあまりが\(\frac{p}{2}\)以上かどうかが影響してくるのでしょうか?
まず、それらの積は\(a\cdot 2a \cdots \frac{p-1}{2}a = (\frac{p-1}{2})! a^{\frac{p-1}{2}}\)となります。そして、オイラーの判定条件によれば、\(\left(\frac{a}{p}\right) \equiv a^{\frac{p-1}{2}}\)です。共通の値が出てきたので、残りは\((\frac{p-1}{2})!\)を\(p\)で割ったあまりと、\(a,2a,\dots,\frac{p-1}{2}a\)のあまりの関係を調べて、\((-1)^{\ell}\)が出てくれば良いことになりますね。
では、ガウスの補題を証明してみましょう。
\(a,2a,\dots,\frac{p-1}{2}a\)を\(p\)で割ったあまりを考えます。そのうち\(\frac{p}{2}\)より小さいものを\(r_1,\dots,r_m\)、\(\frac{p}{2}\)より大きいものを\(s_1,\dots,r_{\ell}\)と表しましょう。数の個数の関係は、\(m+\ell = \frac{p-1}{2}\)です。
すべての\(p-s_i\)は、すべての\(r_j\)と異なることが示せます。仮に\(p-s_i =r_j\)となったとしましょう(背理法)。\(s_i,r_j\)は\(a,2a,\dots,\frac{p-1}{2}a\)を\(p\)で割ったあまりなので、\(s_i \equiv k_{s_i} a \,(\mathrm{mod}\, p)\)、\(r_i \equiv k_{r_j} a \,(\mathrm{mod}\, p)\)と表せます。ここで、\(1\leq k_{s_i} ,k_{r_j} \leq \frac{p-1}{2}\)です。両辺を足せば、\((k_{s_i} +k_{r_j})a \equiv s_i+r_j \equiv p \equiv 0\)です。ここで\(a,p\)は互いに素なので、\(k_{s_i} +k_{r_j} \equiv 0\)です(線形合同式の性質)。一方で、\(2\leq k_{s_i} +k_{r_j} \leq p-1\)で、\(p\)は奇素数なので、\(k_{s_i} +k_{r_j} \not \equiv 0\)で矛盾します。
そして、\(a,2a,\dots,\frac{p-1}{2}a\)は、互いに合同ではありません(仮に合同だとすると、\(a,p\)が\(2\)以上の公約数を持つことになり、仮定に反する)。したがって、あまりもすべて異なることになります。よって、\(r_1,\dots,r_m\)、\(p-s_1,\dots,p-s_{\ell}\)は\(1,2,\dots,\frac{p-1}{2}\)のいずれかに等しいです。したがって、それらの積を計算すると
\[ \begin{aligned} (\frac{p-1}{2})! &\equiv& r_1\cdots r_m (p-s_1)\cdots (p-s_{\ell})\\ &\equiv& r_1\cdots r_m (-s_1)\cdots (-s_{\ell})\\ &\equiv& (-1)^{\ell}r_1\cdots r_m s_1\cdots s_{\ell}\end{aligned} \]
ですが、\(r_1,\dots,r_m\)、\(s_1,\dots,s_{\ell}\)はあまりなので\(a,2a,\dots,\frac{p-1}{2} a\)のいずれかに合同です。したがって、
\[ \begin{aligned} (\frac{p-1}{2})! &\equiv& (-1)^{\ell}a \cdot 2a \cdots \frac{p-1}{2} a \\&\equiv& (-1)^{\ell} (\frac{p-1}{2})! a^{\frac{p-1}{2}} \end{aligned} \]
です。ここで、\(1,2,\dots,p-1\)と\(p\)は互いに素なので、\((\frac{p-1}{2})! \)と\(p\)は互いに素で、合同式の性質により\((\frac{p-1}{2})! \)で割ることができて、
\[ \begin{aligned} 1 &\equiv& (-1)^{\ell} a^{\frac{p-1}{2}} \end{aligned} \]
が得られます。オイラーの判定条件を用いれば、\(\left(\frac{a}{p}\right) \equiv a^{\frac{p-1}{2}} \equiv (-1)^{\ell}\)が得られました。
後半の主張については、「Elementary Number Theory」を参照してください。
平方剰余の第二補充法則とは
ガウスの補題を用いると、平方剰余に関するさまざまな性質が示せます。そのひとつが、平方剰余の第二補充法則(second supplement to quadratic reciprocity)です。
\(p\)を奇素数とすると、次の等式が成り立つ。
\[ \begin{aligned} \left(\frac{2}{p}\right)&= \begin{cases}1 & (p\equiv \pm 1 \,(\mathrm{mod}\, 8) )\\-1 & (p\equiv \pm 3 \,(\mathrm{mod}\, 8))\end{cases} \\ &=(-1)^{\frac{p^2-1}{8}}\end{aligned} \]
ガウスの補題から、第二補充法則を導いてみます。
\(a=2\)として、\(2,2\cdot2,\dots,\frac{p-1}{2}\cdot2\)を\(p\)で割って、そのあまりが\(\frac{p}{2}\)を超える個数\(\ell \)を考えれば良いです。\(2k <\frac{p}{2}\)となるのは、\(k <\frac{p}{4}\)のときで、それを満たす整数は\(\lfloor \frac{p}{4} \rfloor\)個です。したがって、全体\(\frac{p-1}{2}\)からそれを引けば、\(\ell =\frac{p-1}{2}-\lfloor \frac{p}{4} \rfloor\)が得られます。
奇素数は、\(p\equiv \pm 1 \,(\mathrm{mod}\, 8) \)、\(p\equiv \pm 3 \,(\mathrm{mod}\, 8)\)のいずれかに当てはまります。場合分けして考えましょう。
\(p=8k+1\)のとき、\(\lfloor \frac{8k+1}{4} \rfloor= 2k\)なので、\(\ell =4k-2k=2k\)です。
\(p=8k-1\)のとき、\(\lfloor \frac{8k-1}{4} \rfloor= 2k-1\)なので、\(\ell =4k-1-(2k-1)=2k\)です。
\(p=8k+3\)のとき、\(\lfloor \frac{8k+3}{4} \rfloor= 2k\)なので、\(\ell =4k+1-2k=2k+1\)です。
\(p=8k-3\)のとき、\(\lfloor \frac{8k-3}{4} \rfloor= 2k-1\)なので、\(\ell =4k-2-(2k-1)=2k-1\)です。
よって、いずれの場合でも、ガウスの補題\(\left(\frac{2}{p}\right) =(-1)^{\ell}\)より、結論が得られました。
第二補充法則を用いれば、\(2\)が\(p\)を法として平方剰余であるかどうかが、\(p\)を\(8\)で割ったあまりによって判別できます。
例えば、\(p=7,17,23\)のときは\(2\)は平方剰余で、\(p=3,5,11,13,19,29\)のときは\(2\)は平方剰余ではありません。
以上、ガウスの補題、平方剰余の第二補充法則を、具体例を交えて紹介してきました。
ガウスの補題は、平方剰余の相互法則の証明にも使われます。オイラーの判定条件と合わせて、平方剰余に関する重要な性質と言えるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
(2012T)
¥5,437
はじめての数論 原著第3版 発見と証明の大航海‐ピタゴラスの定理から楕円曲線まで
丸善出版 (2014-05-13T00:00:01Z)
¥3,740