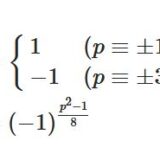平方剰余の相互法則とは例と証明

どうも、木村（@kimu3_slime）です。

前回まで、平方剰余の第一補充法則や、平方剰余の第二補充法則を紹介してきました。

今回は、平方剰余の相互法則について、例と証明を紹介します。

平方剰余の相互法則とは
平方剰余の相互法則の証明
こちらもおすすめ

平方剰余の相互法則とは

平方剰余の相互法則（quadratic reciprocity law）は、平方剰余の性質に関する一般的な等式です。

\(p,q\)を異なる奇素数とする。次の等式が成り立つ。

\[ \begin{aligned}\left(\frac{q}{p}\right)\left(\frac{p}{q}\right) =(-1)^{\frac{p-1}{2}\frac{q-1}{2}}\end{aligned} \]

\(\left(\frac{a}{p}\right)\)は\(a\)が\(p\)を法として平方剰余かどうかを表す、ルジャンドル記号です。

この主張はオイラーによって予想され、ガウスが「整数論（Disquisitiones Arithmeticae）」にて示しました。ガウスは7通りの証明を与えたと言われています。

かなり一般的な主張で、意味するところをつかむのが難しいのではないでしょうか。まずは、いくつか言い換えや具体例を紹介していきます。

\[ \begin{aligned}\left(\frac{q}{p}\right)\left(\frac{p}{q}\right) = \begin{cases}1 & (p\equiv 1 \,(\mathrm{mod}\, 4) または q\equiv 1 \,(\mathrm{mod}\, 4) )\\-1 & (p\equiv q \equiv 3 \,(\mathrm{mod}\, 4))\end{cases}\end{aligned} \]

\[ \begin{aligned}\left(\frac{p}{q}\right) = \begin{cases}\left(\frac{q}{p}\right) & (p\equiv 1 \,(\mathrm{mod}\, 4) または q\equiv 1 \,(\mathrm{mod}\, 4) )\\ -\left(\frac{q}{p}\right) & (p\equiv q \equiv 3 \,(\mathrm{mod}\, 4))\end{cases}\end{aligned} \]

これを平方剰余の相互法則から導いてみましょう。

指数部分\(\frac{p-1}{2}\frac{q-1}{2}\)が偶数なら\(1\)、奇数なら\(-1\)の値を取るので、それを言い換えます。\(\frac{p-1}{2},\frac{q-1}{2}\)が少なくとも一方が偶数なら偶数で、どちらも奇数ならば奇数です。一方が偶数の条件は、\(p-1,q-1 =4k\)を言い換えれば、\(p\equiv 1 \,(\mathrm{mod}\, 4) または q\equiv 1 \,(\mathrm{mod}\, 4)\)です。どちらも奇数という条件は、\(p-1,q-1 =4k+2\)を言い換えれば、\(p\equiv q \equiv 3 \,(\mathrm{mod}\, 4)\)となります。

後半を示します。平方剰余の相互法則の両辺に\(\left(\frac{q}{p}\right)\)をかけて、\(\left(\frac{q}{p}\right)^2 =1\)を使えば良いです。ルジャンドル記号の値は\(\pm 1\)なので、2乗すれば常に1です。

この言い換えによって、ルジャンドル記号を一般のケースでも計算できます。

\(\left(\frac{26}{47}\right)\)を求めたいとしましょう。ルジャンドル記号は乗法的なので、\(\left(\frac{26}{47}\right)= \left(\frac{2}{47}\right)\left(\frac{13}{47}\right)\)です。

\(a=2\)の形が出てきているので、平方剰余の第二補充法則より、\(47 \equiv -1 \,(\mathrm{mod}\, 8)\)なので、\( \left(\frac{2}{47}\right)=1\)です。

もう一方の\(\left(\frac{13}{47}\right)\)は、平方剰余の相互法則よりひっくり返して計算できます。\(13\)を\(4\)で割るとあまり\(1\)なので、符号は変わりません。\(\left(\frac{13}{47}\right)=\left(\frac{47}{13}\right)=\left(\frac{8}{13}\right)\)と、分子分母が減らせました。さらに、\(\left(\frac{8}{13}\right)=(\left(\frac{2}{13}\right))^3 =\left(\frac{2}{13}\right)\)です。再び平方剰余の第二補充法則より、\(13 \equiv -3 \,(\mathrm{mod}\, 8)\)なので、\(\left(\frac{2}{13}\right) =-1\)です。

よって、\(\left(\frac{26}{47}\right)= \left(\frac{2}{47}\right)\left(\frac{13}{47}\right)= -1\)であることがわかりました。

\(a\)を素因数分解し、平方剰余の相互法則、第一・第二補充法則を用いることで、原理的にルジャンドル記号が計算できることになります。非常に強力ですね。

さらに平方剰余の相互法則から、\(3\)が平方剰余かどうかを判定する一般的な条件が導けます。

\(p\)を\(3\)でない奇素数とする。

\[ \begin{aligned}\left(\frac{3}{p}\right)= \begin{cases}1 & (p\equiv \pm 1 \,(\mathrm{mod}\, 12) )\\-1 & (p\equiv \pm 5 \,(\mathrm{mod}\, 12))\end{cases}\end{aligned} \]

まず、平方剰余の相互法則より、

\[ \begin{aligned}\left(\frac{3}{p}\right) = \begin{cases}\left(\frac{p}{3}\right) & (p\equiv 1 \,(\mathrm{mod}\, 4) )\\ -\left(\frac{p}{3}\right) & (p\equiv 3 \,(\mathrm{mod}\, 4))\end{cases}\end{aligned} \]

となります。\(\left(\frac{p}{3}\right) \)については、\(p\)が\(3\)でない奇素数なので、\(p\equiv 1\,(\mathrm{mod}\, 3 )\)か\(p \equiv 2\,(\mathrm{mod}\, 3)\)がありえます。\(p \equiv 2\)のケースは平方剰余の第二補充法則によりわかっていて、

\[ \begin{aligned}\left(\frac{p}{3}\right) = \begin{cases}1& (p\equiv 1 \,(\mathrm{mod}\, 3) )\\ -1 & (p\equiv 2 \,(\mathrm{mod}\, 3))\end{cases}\end{aligned} \]

です。\(\left(\frac{3}{p}\right) =1\)となるケースは、「\(p\equiv 1 \,(\mathrm{mod}\, 4)\)かつ\(p\equiv 1 \,(\mathrm{mod}\, 3\)」または「\(p\equiv 3 \,(\mathrm{mod}\, 4)\)かつ\(p\equiv 2 \,(\mathrm{mod}\, 3)\)」なので、\(p\equiv \pm 1 \,(\mathrm{mod}\, 12) \)です。もう一方も、同様の議論により導かれます。

平方剰余の相互法則の証明

では、平方剰余の相互法則\(\left(\frac{q}{p}\right)\left(\frac{p}{q}\right) =(-1)^{\frac{p-1}{2}\frac{q-1}{2}}\)の証明をしてみましょう。

主な方針は、ガウスの補題によるものです。\(p\)を奇素数として、\(\left(\frac{a}{p}\right) =(-1)^{\sum_{k=1}^{\frac{p-1}{2}} \lfloor \frac{ka}{p}\rfloor }\)が成り立ちます。

これを\(p,q\)に当てはめて計算すれば、

\[ \begin{aligned} \left(\frac{q}{p}\right)\left(\frac{p}{q}\right) &= (-1)^{\sum_{j=1}^{\frac{p-1}{2}} \lfloor \frac{jq}{p}\rfloor }\cdot (-1)^{\sum_{k=1}^{\frac{q-1}{2}} \lfloor \frac{kp}{q}\rfloor } \\ &= (-1)^{\sum_{j=1}^{\frac{p-1}{2}} \lfloor \frac{jq}{p}\rfloor +\sum_{k=1}^{\frac{q-1}{2}} \lfloor \frac{kp}{q}\rfloor }\end{aligned} \]

となります。この指数部分が\(\frac{p-1}{2}\frac{q-1}{2}\)に等しいことを示せば良いわけです。できそうな気がしてきました。

床関数・ガウス記号の\(\lfloor x\rfloor\)評価は、平面上の格子点（\(x,y\)ともに整数となる点）の個数の評価に置き換えられます。

まず、原点を左下の頂点、\((\frac{p}{2},\frac{q}{2})\)を右上の頂点とする長方形の内側\(R\)を考えましょう。長方形の境界は含まないものとします。

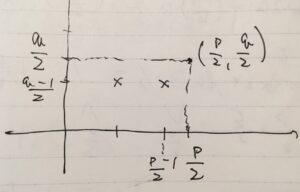
\(R\)の格子点を、タテかけるヨコで考えると、ヨコに\(1,2,\dots,\frac{p-1}{2}\)、タテに\(1,2,\dots ,\frac{q-1}{2}\)の点が並ぶので、\(R\)の格子点は\(\frac{p-1}{2}\frac{q-1}{2}\)個です。

別の仕方でこれを数えます。長方形の対角線を考えて、下側の三角形の内側を\(T_1\)、上側の三角形の内側を\(T_2\)とします。

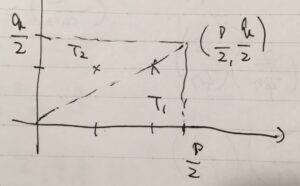
対角線の傾きは\(\frac{q}{p}\)で、\(p,q\)は異なる素数なので、対角線上に格子点はありません。上の図は少しわかりにくいですが、例えば\(p=5,q=3\)ならば、右側の格子点\((2,1)\)は対角線上の点\((\frac{6}{5},\frac{6}{5})\)より下にあります。

\(T_1\)の格子点は、\(\sum_{j=1}^{\frac{p-1}{2}} \lfloor \frac{jq}{p}\rfloor \)に等しいです。\( \lfloor \frac{jq}{p}\rfloor \)は、\(x=j\)における、対角線\(y=\frac{q}{p}x\)の下側にある格子点に等しいので。例えば\(p=5,q=3\)ならば、\( \lfloor \frac{1\cdot 3}{5}\rfloor =0 \)、\( \lfloor \frac{2\cdot 3}{5}\rfloor =1 \)で、\(T_1\)に含まれるのは1個ですね。

同様にして、\(T_2\)の格子点は、\(\sum_{k=1}^{\frac{q-1}{2}} \lfloor \frac{kp}{q}\rfloor \)に等しいです。\(x,y\)軸を入れ替えたと見れば良いです。

以上により、長方形\(R\)の格子点の個数\(\frac{p-1}{2}\frac{q-1}{2}\)は、\(T_1\)の格子点の個数\(\sum_{j=1}^{\frac{p-1}{2}} \lfloor \frac{jq}{p}\rfloor \)と\(T_2\)の格子点の個数\(\sum_{k=1}^{\frac{q-1}{2}} \lfloor \frac{kp}{q}\rfloor \)の和に等しいことがわかりました。

よって、ガウスの補題による計算に戻れば、\(\left(\frac{q}{p}\right)\left(\frac{p}{q}\right) =(-1)^{\frac{p-1}{2}\frac{q-1}{2}}\)が示せました。

以上、平方剰余の相互法則について、応用例と証明を紹介してきました。

「平方剰余で表せるか？」という問題を、オイラーの判定条件やルジャンドル記号で言い換えた上で、平方剰余の相互法則は非常に一般的な回答を与えてくれます。しかも、記号のおかげはありますが、かなりシンプルな形の主張になるのが驚きですね。

木村すらいむ（@kimu3_slime）でした。ではでは。