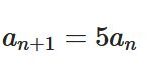
「微分方程式論」の記事一覧
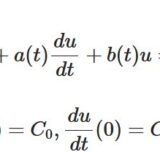
線形微分方程式はなぜ指数関数e^{λt}と仮定して解いて良いか

微分方程式の解でなぜ指数関数(exp・ネイピア数)が現れるか
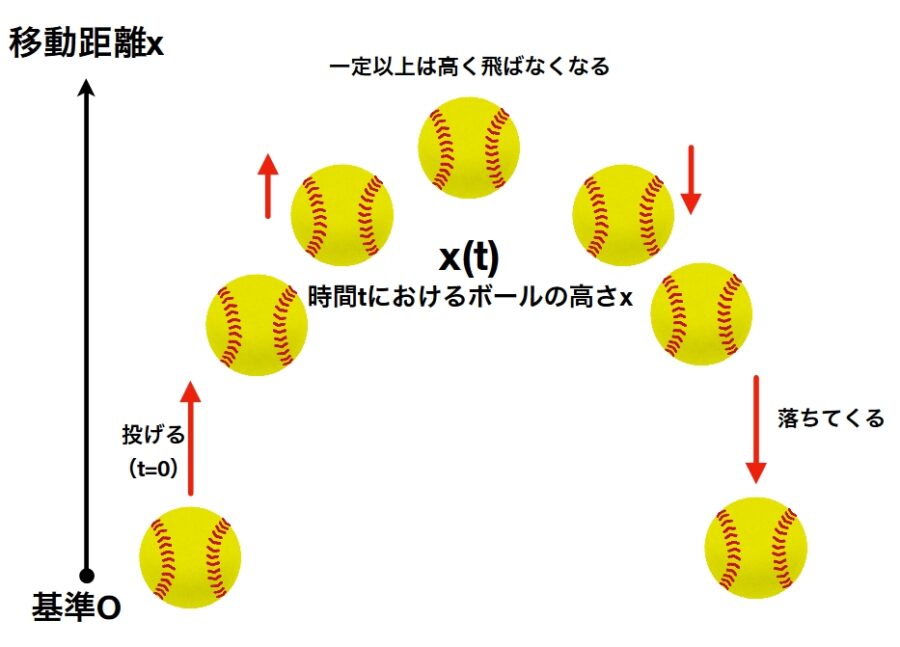
不定積分と定積分をなぜ学ぶか 微分方程式の一般解と特殊解
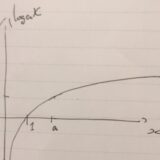
対数logの外し方、外せる条件と対数関数の性質
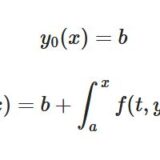
完備性とは:無理数、微分方程式の解の近似を例に
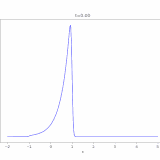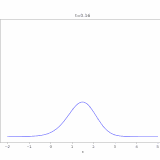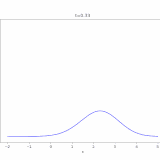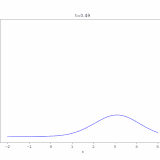
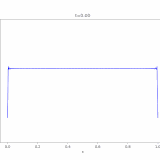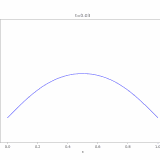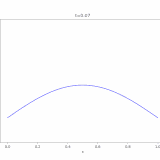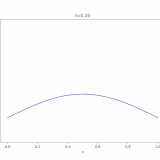
移流拡散方程式、その解き方:熱方程式への関数変換
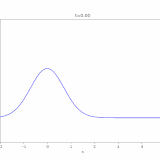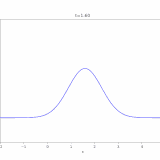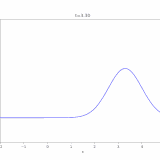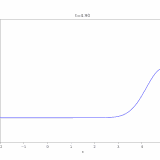
移流方程式(輸送方程式)とその解き方を解説
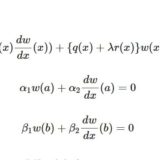
ストゥルム・リウビル型微分方程式の発見:熱方程式から
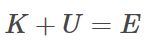
力学的エネルギー保存の法則を、微積分で導出・証明する
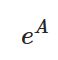
線形常微分方程式を行列で解く:行列の指数関数を解説
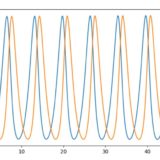
ルンゲ=クッタ法:常微分方程式をPythonで解く原理を解説
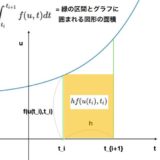
オイラー法:常微分方程式をPythonで解く原理を解説
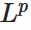
なぜルベーグ積分を学ぶのか 偏微分方程式への応用の観点から
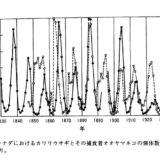
食う-食われるの数学:捕食者-被食者モデル(ロトカ・ヴォルテラ方程式)とは?
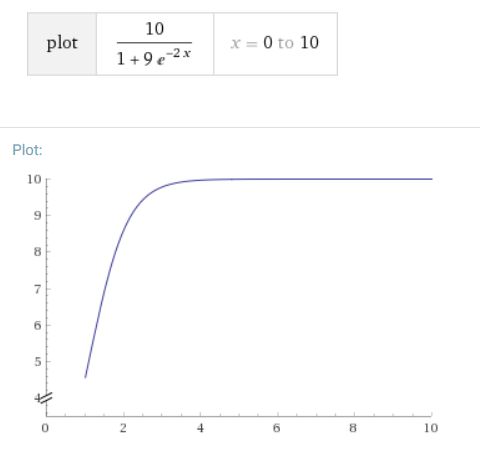
生物の増え方を予測:ロジスティック方程式とは?
波の重ね合わせの原理はなぜ成り立つ? 波動方程式入門
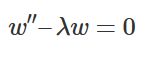
同次形の2階線形微分方程式の解き方、学ぶ意味:熱方程式への応用を例に
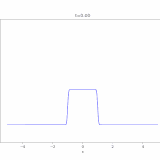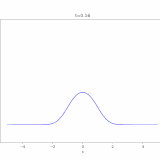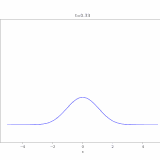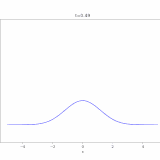
熱方程式の解き方:フーリエ変換(全空間、N次元)