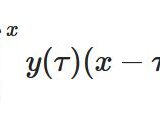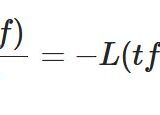どうも、木村(@kimu3_slime)です。
数学の定義や概念を学ぶときに、「なぜこう定義するのだろう」と疑問に思うことはよくあります。
決まりきった答えのない疑問ですが、自分なりに考えを整理するのは大事です。そこで今回は、僕なりの疑問の解決法、学習法を紹介したいと思います。
まずは何が書かれているか理解する
まず前提として、「なぜこう定義するのか」と適切に問うためには、「何が定義されているのか」を正確に読み書きする力が必要です。
数学的に何が書かれているのかわからないのに、「なぜ」を考えると埒が明かず、不毛な時間を過ごすことになりやすいでしょう。
参考:数学の本・文章・数式・記号の読み方:意味を意識して読む
例えばサインやコサインなどの三角関数は、「なぜそんなものを考えるのだ、学ぶ意味はない」と考える人をよく見かけます。
純粋な「なぜ」ではなく、「私はこんなものを理解できない、だから学ぶ意味はない、なぜそれを学ぶのか」と思うケースはあるのでしょう。僕も、難しい内容に出会ったときに、なぜこんなことを学ぶのか、と考えがちです。
「難しい」から「なぜ」と問うているなら、まず言葉の定義を本できちんと確認すると良いでしょう。定義に含まれている言葉のひとつひとつ、自分に説明できるか、考えてみてください。
実は、その定義の前提となる基礎知識がないから、難しいと感じている可能性はあります。数学は積み重ねの学問なので、定義に何が書いてあるか読めないレベルならば、きちんとわかるところまで遡った方が、結果として多くのものが得られるでしょう。
定義には使い道がある
さて、定義に書いてあることはわかったが、いまいちピンと来ない。なぜこんな風に定義するのか、一体これは何なのか、といった疑問への対処法を紹介します。
基本的には、定義の使い道を考えることです。
具体化する
最初にして最強のコツは、定義を満たす例を具体的に書いてみる、ということです。
数学の定義は、しばしば抽象的です。特に大学数学以降ではその傾向が強まり、親切に書かれていた具体例が少なくなっていったりします。
簡単な例を考えましょう。
整数\(m\)が偶数であるとは、\(m\)が2で割り切れることと定義する。
で、偶数とはなんでしょうか。2で割り切れる数を考えれば良いわけです。\(2,4,6,8\)は偶数です。\(10000\)も偶数です。
「割り切れる」という言葉の意味を適切にわかっていることが大事です。\(0= 2\cdot 0\)なので、\(0\)は偶数です。\(m\)は整数と書かれているので、\(-2,-4,-6,-8\)と負の偶数も考えられます。
このように具体例を考えたり、調べたりすることで、「一体何を考えようとしているか」という疑問は解決するでしょう。
参考:手の付け方がわからない数学の問題の解き方:定義を確認し、単純化しよう、大学の数学の勉強についていけなかった経験談、その解決法
「関数\(f\)が微分可能とは」「集合\(X\)が線形空間とは」といったように、定義においてはしばしば文字・記号が使われます。
まず最初に、\(f,X\)といった記号の簡単な例を考え、その定義を満たすかチェックしてみましょう。数字が含まれていたら、\(a=0,1\)としたり、\(N=1,2\)と小さい特殊な数字を考えることで、形が簡単になることが多いです。例を集めていくことで、定義が指し示したいものがわかるようになるでしょう。
参考:抽象ベクトル空間・線形空間の具体例R^N:順序対と直積集合
性質を調べる
数学の文章では、筆者はしばしば結論をあらかじめ知っていて、良い性質や期待する結果を踏まえて、論理的な順序を踏まえて定義をすることがあります。このようなやり方は、天下りの議論と呼ばれるものです。
例えば次の定義を考えましょう。
関数\(f,g\)の畳み込み(合成積 convolution)\(f*g\)は、
\[ \begin{aligned}(f*g)(t):= \int_0^t f(\tau)g(t-u)d\tau \end{aligned} \]
と定義される積分です。
一体なぜこんな定義をするのでしょうか。僕はそんな疑問を抱いたら、教科書のページを先に進めて、それを使った良い性質や定理がないか探します。その結果を導くために定義をしていることが多いのです。
このように定義をする理由のひとつは、ラプラス変換について
\[ \begin{aligned}L(f*g)=L(f)L(g)\end{aligned} \]
が成り立つからです。積\(L(f)L(g)\)を計算する中で、自然と上の定義は導かれます。その結果を知っているから、最初に定義をしたわけです。
線形空間では、内積という概念を考えます。その利用としては、ノルムや長さを導いたり、ベクトルや行列の直交性があります。例えば、グラム・シュミットの直交化法は、内積の応用例です。
参考:ユークリッド空間R^Nの内積、ノルム、距離について解説
このように、基礎的な定義が登場したら、その先でどんな応用があるのか、読み飛ばして先の内容を確認すると良いでしょう。定義はその後の議論で使うために最初に宣言されるものです。したがって、その後の内容、使い道を知ることで、定義や理論の意義が読み取れることもであるでしょう。
参考:なぜルベーグ積分を学ぶのか 偏微分方程式への応用の観点から
特に大学以降の数学では、定義ひとつを点として理解するだけでなく、定義とその性質・定理を関連付け、体系的に理解していくことが大事になっていきます。
もし定義の意義に疑問を抱いたら、自分でその使用例や性質を探し、概念同士の関連性や、狙いとする定理、話の目的を考えて整理してみると良いでしょう。
参考:数学の勉強法:眺めるな、書いて考えよ、自分の数学を作ろう、受験勉強と大学の勉強の違い:数学や物理の体系的な学びとは
数学外への応用を調べる
何のために数学の定義や概念を学ぶのか、より広い視点を得るには、その応用例を調べたり考えたりすると良いでしょう。
例えば三角関数はバネの運動(周期的な運動)の表現に使えますし、微積分は運動の分析、物理学・力学の理解に役立ちます。
参考:サイン、コサインは何の役に立つ? バネの振動と三角関数
このサイトでは、「なぜ~~を学ぶのか」というタイトルで、数学外への応用を紹介しています。
参考:なぜ中学数学で関数を学ぶか:数理モデルの考え方、なぜ中学・高校数学を学ぶのか 数理モデルとしての微分方程式、なぜ線形代数を学ぶ? Googleのページランクに使われている固有値・固有ベクトルの考え方
ただし、数学外への応用は数学の教科書には書いていないことも多いので、学びはじめのときに調べるのは難しいです。
一旦、先程までの段階(定義の具体化、性質を調べる)レベルの理解をした上で、余裕があったら調べてみると良いでしょう。図書館や本屋で、いろいろな教科書を当たると良い本に出会えるかもしれません。
数学に限ず幅広い好奇心を持ち学んでいると、他で得た学びが結果として数学の理解に役立つことでしょう。
以上、数学の定義で「なぜ」と疑問に思ったときの学習法を紹介してきました。
まずは定義を読むための基礎知識を確認すること、その後は定義の使い道を調べて考えることをおすすめします。
「なぜこんなことを考えるのか」という疑問は、考えすぎて解決しないこともありますが、自分で考えること自体は大切です。今回の話が、疑問を解消するきっかけになれば嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
こちらもおすすめ
手の付け方がわからない数学の問題の解き方:定義を確認し、単純化しよう
なぜ線形代数を学ぶ? Googleのページランクに使われている固有値・固有ベクトルの考え方