大学の数学の勉強についていけなかった経験談、その解決法

どうも、木村（@kimu3_slime）です。

今回は、僕が大学の数学の勉強に最初ついていけなかった経験談と、その解決法を書いていきます。数学に限った話題でなく広く理系、大学という場の話がメインです。ごく個人的な話なので、万人の参考になるかはわかりません。

大学入学したての自分が、こんなことを知っていれば苦労しなかったのに……（笑）という気持ちの備忘録です。

数学の独学に特化した話はこちらで：大学数学を独学するための方法・考え方

学びたいこと・やりたいことが曖昧で、バラバラだった
講義・教科書のペースに合わせて受動的だった
- 講義選びは教科書選び、教科書選びは図書館で
- 講義で教えてもらうのではなく、自分で学ぶしかない
独学に自信がつくまで
まとめ
こちらもおすすめ

学びたいこと・やりたいことが曖昧で、バラバラだった

勉強の中身の話をする前に、まずは勉強以外の僕の生い立ち話から入ります。

とにかく、大学1年生のときはドタバタとして、勉強そのものに集中できていませんでした。

僕は群馬県の高校を出て、東京都内の大学に入学しました。大学の近くにアパートを借りて、親元を離れて下宿生活です。一人暮らし特有の面倒さはありますが、自分の自由なリズムで生活できて、総じて快適でした。

問題は勉強です。

何を学びたいか、ふわっとしていました。少なくない大学生はそういうものかもしれません。モラトリアム自体は悪いことではないと思いますが、勉強の面では遅れを取ります（笑）。

もともとは中学生頃から、学校の勉強は好きではありませんでしたが、数学に限っては何もせずともできる方でした。高校生の頃に、地球温暖化に関する啓蒙的なビデオを見て、世界はやばいことになってるのかと衝撃を受けた反面、「本当なのだろうか？」と疑問に思い、人間の科学活動全般に興味を持ちました。社会の問題を読み解くためには科学の知識が必要だろう、そのベースには数学があるはずだ。また、生意気なことに人より頭は良いと思っていたし、その力で社会の役に立ちたい、……そのための数学的素養を身につけたいと思うようになりました。これが大学進学、数学科を進路として選んだひとつの理由です。

数学以外にも色々な学問を学びたいとは思っていましたが、数学を基礎としてやっておけば、他の分野の本を読むにも困らないという応用性が魅力でした。もし人文系の科目が得意だったら、哲学科に進んでいたかもしれません。数学をやっておけば、金融関係の仕事でも、プログラマーでも、何かしらできるだろうと。数学の研究をしようという発想は、この時点で全くありませんでした。

受験勉強は、高校2年の終わりから始めて、ゲームで培った攻略感覚を駆使して、ぐんぐん成績を伸ばして突破しました。とはいえ、受験科目の中で得意・楽しかったのは英語です。数学は正直センター試験のレベル止まりで、記述式は不得意だったと思います。

高校内では模試や入学した大学の偏差値の面で1番の成績でしたが、そんなことは相対的なもので、大学に入れば関係ありません。数学に関しては、同級生に対して遅れを取っていたと思います（これは後でまた言及します）。

いよいよ大学に入って、履修登録なるものが始まり、よくわからないままとりあえず色々な講義を取ることにしました。これも失敗だったと思います。

通っていた大学のシステムでは、1年生はざっくりと学部に所属して教養科目を学び、2年生に入る時に進路振り分けがあって学科に所属することになります。僕の場合、1年生で理学部への所属です。

教養科目として多くの講義を受けること自体は良いです。ただし、過密なスケジュールにすれば、個々の科目の理解が追いつきません。興味のある程度の科目は、履修せずに、講義にもぐるだけで良かったのです。大学前期はこれで失敗しました。

数学に関しては、微積分と線形代数の講義がありました。確か、微積分が単位ギリギリの点数、線形代数に至っては落としたような気がします。

「数学科に所属するつもりなのに恥ずかしくないの？」という思いはありますが、講義の取りすぎであったこと、数学の勉強にそれほど時間を割いて（割けて）いなかったので、後になって思えば気にすることではないかと思います。

自分の専門以外の学問、教養科目もまた楽しいものでした。特に地球惑星科学や意思決定理論は、それまでの僕の知らない分野でしたが、数理の活用として面白かったです。

また、講義に合わせて、マルチタスクを処理するのに苦戦していました。

たまたま入ったサークル活動でやることもありますし、（詳しくは書きませんが）家族の事情に悩んでいた時期でもありました。

趣味でゲームするのに時間もかけていたし、学校の勉強とは関係なくいろいろな本を読んでいました。そんな中で出会ったのが、タスク管理術、GTDという考え方です。大学生や社会人は、誰であってもやること＝タスクの管理をする方法を学ぶのをおすすめします。GTDでは、勉強に関することだけでなく、人生全般でやりたいことを見直して、やることとやらないことがはっきりさせられて良かったです。いくらやりたいことが多くても、実際にやらないと意味ないんですよね……。

僕は「はじめてのGTD ストレスフリーの整理術」を読み、それを実践しはじめてから、「どの科目にいつまでレポートがあって…」と迷うことなく、タスク管理ツールで順に処理できるようになりました。僕は今でも（メモ帳：Dynalistで）タスク管理をしながら仕事をしています。

講義・教科書のペースに合わせて受動的だった

高校と大学の学びの大きな違いをひとつ挙げるならば、主体性以外の何物でもありません。受け身で講義を聞いているだけでは、高校までなら大丈夫かもしれませんが、大学では振り落とされます。

僕が大学（学部）を出て良かったと思うのは、この学ぶための主体性を得られたことです。これは一生の財産になります。

大学入学したての僕ならば、「主体性が大事と言われても、そんなの僕にはないしどうすれば良いんだ」と思うでしょう。なのでもう少し具体的に話していきます。

講義選びは教科書選び、教科書選びは図書館で

先ほども書きましたが、自分が取る講義を選び、履修登録する時点から主体性が求められています。

卒業要件は何か、自分の興味のある講義なのかどうか、自分で調べて確認していく必要があるでしょう。講義の最初の数週間はお試し期間です。「講義は取らなければならないもの」ではなく、「取りたい/取るべき講義を取る」と選びましょう。あれもこれもやりたいというのは、それを実践できる力がない限り、何も選んでいないのと同じです。

講義を取るべきか判断するときに、その講義に出席することも大事ですし、友達に講義の評判を聞くのも良いですが、教科書選びが何より大事です。むしろ教科書選びを通して、その講義の全体像を想定し、必要かどうか判断するのが良いでしょう。何せその分野の知識がないのが普通ですよね、そして知識を得るためには教科書をあたるのが近道です。

僕は最初は、シラバスや講義で提示されていた教科書のみをチェックしていました。数学に関しては自分用に教科書も買ったのですが、それでも不足していたと思います。

自分が学ぼうとしている分野がどういうものなのか、一冊の本から飲み込むのは至難の業でしょう。高校までは教科書1冊で勉強が済んでいまいたが、大学はそうではありません。高校では学習指導要領があり、学ぶ内容が全国統一され、参考書で扱う話題も似てきます。一方で、大学では同じ「微積分学」「線形代数学」でも、内容に共通する部分もあれば、全く違う部分もあります。学ぶ順序も教科書によってバラバラです。理学部向けと工学部向け、数学科向けと物理学科向けでは重点が違ったりします。

教科書を選ぶための良い方法は、図書館に行くことです。大学の図書館は、一般の書店に比べて、当たり前ですが専門書が桁違いに充実しています。たとえ話ですが、書店で微積分の本が20冊なら、図書館には200冊あります。選択肢が多い方が、当然自分に合った本が見つかる確率はあがるのです。

大学の図書館に入って、学ぼうとしている分野の本棚に行ってみてください。いくつかの本にしぼって取り出し、机の上に広げて、雰囲気をつかみましょう。具体的には、目次を見比べてみましょう。どういう単語がどんな順番で出てくるのか、共通する話題とそうでない話題は何か、だんだんと見えてくると思います。講義ではおそらくこのへんまで扱うんじゃないか、と予測するのも良いでしょう。また、まえがきを読めば事前に必要な知識が書かれていることもあるので、もし不足しているならそちらもチェックします。

良いと思った本は借りて、長期的に使えそうだなと思ったら書店で購入しましょう。これで講義を選択するための方法、履修する前の準備はできると思います。（講義なしで教科書を読んで、先取りしているのが理想です。）

教科書選びに：「趣味の大学数学」おすすめ教科書・参考書・入門書

講義選択のための教科書選びならばこれで十分ですが、自分の専門としたい分野があるならば、もう少し広い目を持って図書館を活用すると良いでしょう。例えば数学ならば、数学の棚全般を見ていけば、どんな分野があるのかわかります。興味に応じて手にとって、キーワードに馴染んでいきます。わからないなりに面白いものもあるでしょう。だんだんと、数学全体の分野にどういうものがあって、どう関連しているかもわかってくると良いですね。

僕が作った大学数学のロードマップも参考になると嬉しいです。

参考：大学数学のロードマップ～分野一覧と学ぶ順序

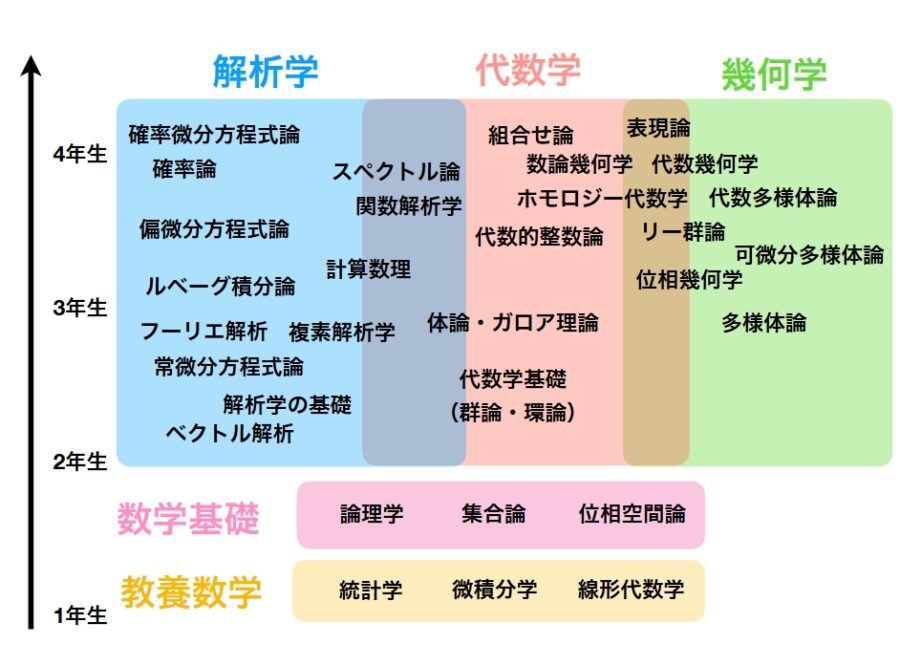
これは参考程度で鵜呑みにせず、自分で本をチェックして、必要性や関連性を見抜ける力が大事です。ここまで来れば、大学図書館がどれだけありがたいものかわかります。

講義で教えてもらうのではなく、自分で学ぶしかない

大学で講義を受けたことがある方は同意してもらえるのではないかと思いますが、講義には当たり外れがあります。

日本の大学で授業を教えているのは、普通は研究者です。研究者は研究実績とその評価によって採用され、講義能力が（小中高の教員のように）特別に問われるわけではありません。つまり、教えるスタイルはバラバラで、上手い下手もありますし、好み（合う合わない）もあります。

特に1年生の科目は履修者が多く、大人数の講義になりがちで、そうすると一方的な板書が中心となり、学生がついてきているかどうか気にされにくいです。

板書のスピードが速いと、書き写すので精一杯で、とても理解することができません。教える側の言い分として、予習していて当然、だからスピードを出しているといったものがあります。言われればそうなのかもしれませんが、高校から大学に入りたての自分にはそういう意識がありませんでした。それだけ大学で学ぶ内容にはボリュームがあり、その内容が短い時間に詰め込まれがちです。講義だけでは理解できない可能性も含め、教科書選びは大事になります。

とはいえ単位は必要です。講義の点数は点数、理解度は理解度と、ある程度わりきっても良いのではないでしょうか。点数の取りやすい単位とそうでない単位はあります。卒業条件、大学院への推薦、奨学金の返済免除など、良い成績を残すために点数は必要です。点数と理解度は、必ずしも比例しません。深く理解できて点数も取れる人は良いのでしょうが、僕はそうではありませんでした。

大学1年生の後期は、その点を割り切りました。これまた数学科に進むのに呆れられるかも知れませんが、線形代数と微積分の講義は取らず（笑）、独学に移行しました。（2年生での学科の所属では成績上位者が優先されるため、取得単位の平均点を上げたいという理由もありました。）

もちろん、数学の勉強をやめようと思ったわけではありません。ただ、講義のペースについていけない部分が多かったので、自分のペースで基礎固めをしようと思ったのでした。そのやり方が最短だったか、正解だったかといえばわかりませんが、「数学がわかっていない」ことを自覚し、自分なりのやり方を確立しようとした、この点は主体性の芽生えがあると言えるのではないでしょうか。確か、図書館でいろいろな本を探し始めたのも、この時期だった気がします。難しい教科書よりも、具体的な演習書から手につけていきました。

学びというのは、本来カリキュラムなど関係ないものです。特に数学は、その性格上、自分がわかっていない部分が生まれれれば、その無理解はその先にまで影響してきます。一度置いていかれると、取り戻すのが難しい。しかし、大学に入りたての頃は、講義という枠組みに流され、授業に出て板書を写すだけで勉強した気になり、いざと問題となるとほとんど解けないような学生でした。結局のところ学問は自分で勉強するしかなく、講義はそのサポートをするにすぎないのだ、と僕は考えています。（むしろ、講義に出て勉強した気になって、頭を使わず受動的な作業をしていた……となるケースもあるので気をつけましょう）

（数学科の専門科目では、自分で勉強していれば、試験に出てくれれば別に講義は出なくても良いよ、というスタイルが多かった気がします。数学科の非常によくできる人は、想像できないほど遥かに先の内容を学んでいるものです。それこそ中学高校のうちから大学数学やってる人がいるので。とはいえ人がどれだけ進んでいようが、自分は自分の学びをしましょう。勉強になると思った講義は出たほうが良いと思います。）

独学に自信がつくまで

僕は大学1年生の数学で、具体的にどこでつまづいたか。

微積分では、いわゆるイプシロン-デルタ論法の話がわかりませんでした。連続性の定義自体がやろうとしていることはわかる気がするのですが、自分の手で証明することができないのです。特に、上限や下限といった議論が難しくて絶望した覚えがあります。中間値の定理やテイラー展開が出てくるあたりになると、高校で見覚えのある微積分になってきて、公式を覚えて当てはめる式の計算でどうにかなりました。

線形代数では、行列式のあたりでつまづきました。難しいというよりは、行列をひたすら計算させられるような印象があり、面白いと思えませんでした。また、2,3次元でなく、\(n\)を使うのが普通になります。こうした一般的な文字を使った計算や証明の方法に自信がありませんでした。例えば与えられたベクトルが一次独立であることを示せ……といった問題は、なんとなく書けたものの、それが正しい記述なのか不安でした。

また、講義も教科書も、高校までの親切なスタイルと違い、定義・命題・証明のスタイルになりました。このスタイルに慣れ、何を言っているのか納得して読めるようになるまで、随分な時間を必要とした気がします。

参考：大学数学の教科書の読み方、最初に「定義・命題・証明」を知ろう、数学の証明とは何か、なぜ必要なのか？

結局高校までの数学で身についていたのは計算スキルで、論証、証明の能力は全くありませんでした。いわゆる証明問題って、解法のパターンを覚えるものなんでしょ……といった感覚です。大学の数学を理解するためには、仮定から結論を導くことを、教科書に書いてあることを写すのではなく、自分の言葉でできるようになる必要があるのです。

そのために、僕には論理と集合に関する勉強が足りていませんでした。「集合と位相」は数学科では2年生で学ぶことになっていますが、1年生から教科書を読み始めました。高校のレベルの集合の理解では、大学数学には不足していると思います。

松坂「集合・位相入門」は、かなり証明や説明が詳しいので読みやすかったです。ただし論理の知識は前提となっているので、その点では後に知った「論理と集合から始める数学の基礎」を読むと良いでしょう。

論理と集合の言葉の扱いに慣れてから、微積分や線形代数の本を読むと、何が書かれているのか、どうやって論理を積み重ねているのか、読み解くことができるようになりました。こうして、僕は大学1年の数学苦手を突破した気がします。

今になって思えば、「数学の基礎である論理学・集合論を先に学び、その後に線形代数や微積分を学べ」とどうして誰も教えてくれなかったのか？という気持ちになります（笑）。先に……とまでいかなくとも、同時並行で進めるのは確実に理解を深めます。僕には、この経路を通らずに、線形代数や微積分（の抽象的な議論）が理解できた気がしません。地に足をつけて深く大学数学を学びたいなら、論理学や集合論を学び始めるのをおすすめします。

参考：論理学の入門ロードマップ：大学数学に必要な論理学とは

そうして独学をするうちに、自分用のノートが作れるようになりました。教科書に書いてあることを写すのではありません。定義などはそのまま写すかもしれませんが、自分なりにわかりやすい記法、言葉遣いに直します。そして教科書の省略されている部分、曖昧な部分、自分のわからないことを探しては理由を考えてノートに説明を書きます。行間を埋める作業、というやつです。内容が抽象的でわかりにくければ、簡単な具体例を自分で作りましょう。教科書の記述や問題はほぼ100%難しいです。バカみたいに簡単な例を考えることが、実は理解につながります。

独学の方法は、別の記事で詳しく書いています。最終的に、自分で作ったノートが、自分にとっての最良の教科書になるでしょう。

参考：数学の学びを深めるために必要なのは、「わからない」と言える力、大学数学を独学するための方法・考え方

もし大学数学のある単元でつまづいたら、そこで悩みすぎないほうが良いと思います。もちろん粘り強く考えることは大事です。しかし、一旦遠回りするのも良いと思います。僕は微積分や線形代数の本でわからないと感じていたので、集合論に迂回し、そして戻ってきました。他の分野で理解できることを増やしてからもとの問題に戻ってくると、意外とあっさり理解できたりします。

独学をしていれば、講義や教科書は、前から順番通りに読む必要は必ずしもないことに気づきます。特に数学の教科書は、その論理的な構成のために抽象的な定義から入りがちですが、それが理解しやすい順序であるとは限りません。手に届く、自分の言葉として扱えるレベルの部分から入っていきましょう。

教科書の全体が読めるようになってきたら、この分野は何をしたいのか、定義や定理の意義や、概念間の関係を考えるようになってくるでしょう。そこまで見えれば、自分だったらこの分野はこの順序で学ぶ/教える……と、自分なりのカリキュラムが組めるはずです。完全ではなくとも、単に教科書で学ぶ側から、それを身につけて、やがては自分なりの解釈や意義付けをして教えられる側になっていく。大学の学部では、このレベルの主体性が身につけば良いのではないでしょうか。