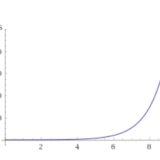
「2018年7月」の記事一覧
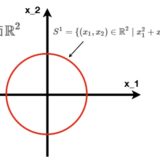
集合論入門:集合の定義、数の集合、ラッセルのパラドックス

「趣味の大学数学」は、厳密化・抽象化だけをありがたがらない

「趣味の大学数学」おすすめ教科書・参考書・入門書
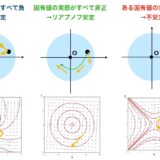
微分方程式の安定性を調べる「線形化」の方法とは?

線形微分方程式の解の安定性は「固有値」を調べればわかる
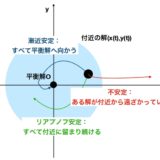
方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門
なぜ重積分を学ぶ? 熱伝導方程式の導出を例に
なぜ偏微分を学ぶ? フーリエの熱伝導方程式を例に

集合論のはじまり、全称命題と存在命題、論理記号を知ろう
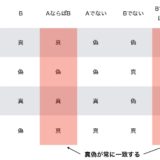
「AならばB」のよくある誤解から学ぶ、論理学入門(対偶、逆、否定、真偽表)
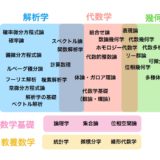
なぜ教養数学として微積分学と線形代数学を学ぶのか ブルバキが現代数学に与えた影響

カオス理論、バタフライ・エフェクトとは何か? ローレンツ・アトラクターを例に
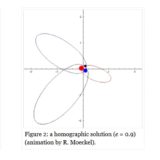
惑星の運動は数学的に「解けない」? 多体問題から力学系理論へ
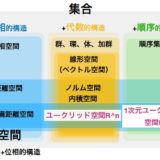
集合、構造、空間とは何か? ユークリッド空間R^Nを例に考える
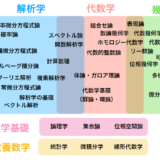
大学数学のロードマップ ~ 分野一覧と学ぶ順序
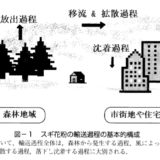
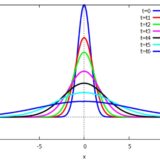
花粉の広がりを数式で予測する、拡散方程式とは

「数学は何の役に立つのか」「じゃあ学問は役に立つためにあるのか?」
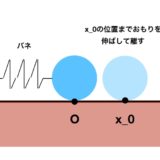
サイン、コサインは何の役に立つ? バネの振動と三角関数