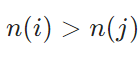
「位相空間論」の記事一覧
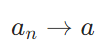
完備な距離空間の閉集合は完備であること、逆の証明
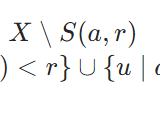
距離空間の球面が閉集合であることの証明
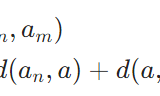
距離空間において収束列がコーシー列であることの証明
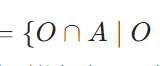
相対位相、部分集合における開集合・閉集合とは:ユークリッド空間の位相を例に

位相の強弱とは:密着位相と離散位相を例に

閉集合、触点、閉包、集積点、孤立点とは:定義、性質、例
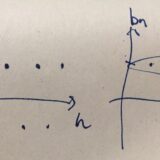
部分列、ボルツァーノ・ワイエルシュトラスの定理とは:点列コンパクトとの関係

連続関数とは:イプシロンデルタと開集合、閉集合による特徴づけ

ユークリッド空間における開集合、閉集合の性質:実数の区間を例に
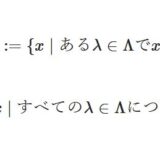
集合族の扱い方(和集合・共通部分):実数の区間を例に
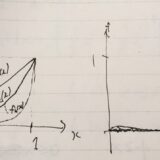
関数列の収束:各点収束、一様収束、L^p収束とは
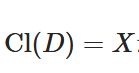
稠密性とは:有理数、ワイエルシュトラスの近似定理を例に
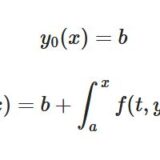
完備性とは:無理数、微分方程式の解の近似を例に
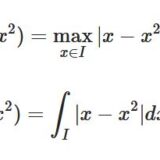
距離空間とは:関数空間、ノルム、内積を例に
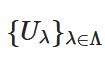
コンパクト性とは:有界閉集合、最大値の定理を例に
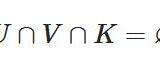
連結性とは:実数区間、中間値の定理を例に
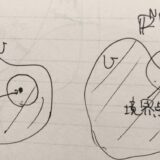
ユークリッド空間の開集合、閉集合、開球、近傍とは何か?

「はじめよう・解いてみよう位相空間」レビュー