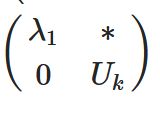
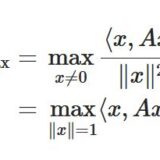
対称行列のレイリー商とは:最大・最小固有値との関係

2次形式、正定値行列とは:2変数関数の極値判定を例に
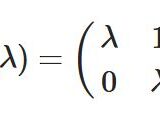
なぜジョルダン標準形を考えるか、求め方、一般固有ベクトル
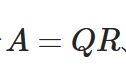
QR分解とは:シュミットの直交化法による求め方
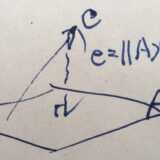
最小二乗法とは:最小二乗解の求め方、正規方程式、射影による理解
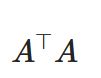
グラム行列A^T Aとは:具体例、性質

行列の対角化可能性と同値な条件とは:証明、判定法
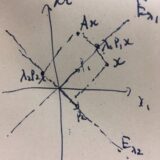
対称行列のスペクトル分解とは:具体例、証明
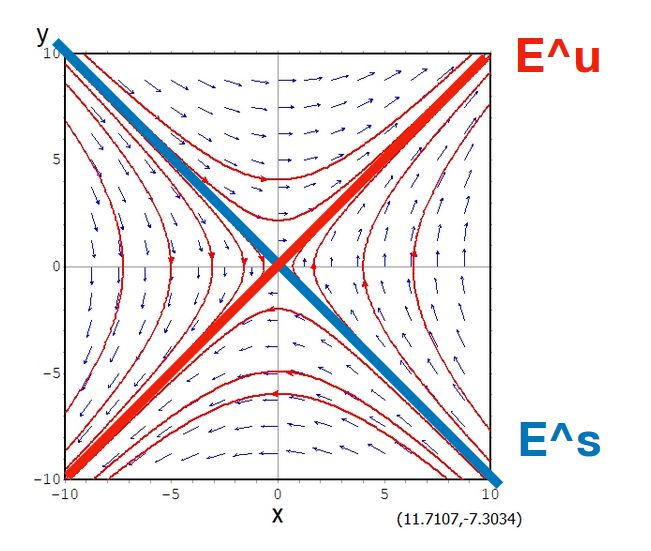
不変部分空間とは:固有空間、射影行列を例に
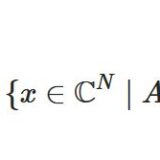
固有空間の求め方、代数的・幾何学的重複度とは:部分空間となることの証明
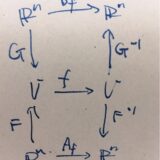
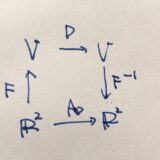
線形写像のランク、行列式、固有値は表現行列によらず定まることの証明
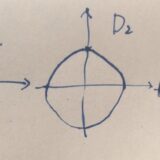
pノルムとは:絶対値ノルム、最大値ノルム、同値なノルム
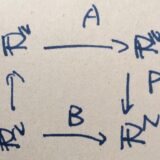
行列の相似とは:対角化との関係、不変量(ランク、行列式、固有値)
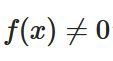
連続関数はゼロでない点の近傍でゼロでないことの証明
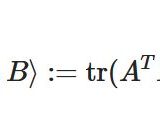
行列のフロベニウス内積とは、性質:回転行列のなす角度を例に
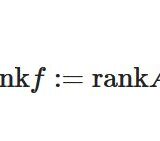
線形写像の単射・全射・全単射の判定:ランクによる求め方
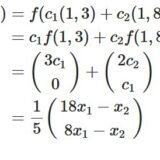
線形写像の求め方:基底の行き先で一意に決まる
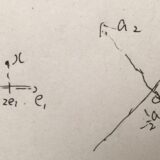
線形写像の表現行列、基底の変換の求め方を解説