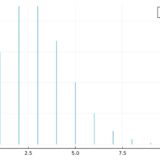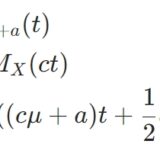
「応用数学」の記事一覧
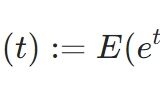
モーメント生成関数とは:正規分布の平均と分散を例に
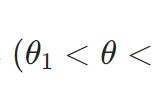
区間推定、信頼区間とは:分散既知の正規分布における平均の推定を例に
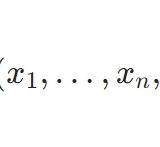
最尤推定法、尤度とは:ベルヌーイ分布を例に
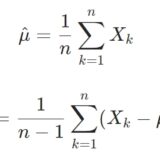
点推定、不偏推定量とは:平均と分散を例に、なぜn-1で割るのか

統計モデル、統計的推測、パラメータ、統計量とは
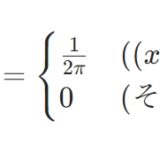
共分散0(無相関)だが独立でない確率変数の例
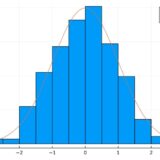
中心極限定理とは:Juliaでの計算例、意味
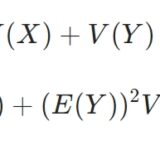
2変数の確率変数の分散とは:和と積の性質、証明
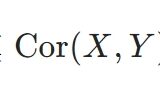
確率変数の相関係数が-1以上1以下であることの証明
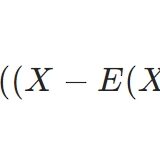
2変数の確率変数の共分散、相関係数、共分散行列とその性質
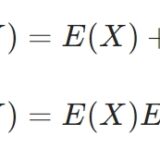
2変数の確率変数の期待値とは:和と積の性質、証明
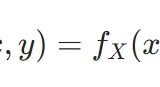
確率変数の独立性とは:具体例、性質
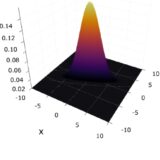
2次元の正規分布、分散共分散行列とは:具体例をもとに

2変数の連続同時確率分布、周辺分布とは:一様分布を例に
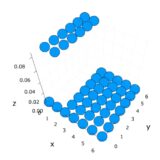
2変数の離散同時確率分布、周辺分布とは:一様分布を例に
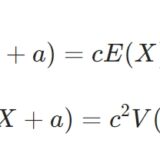
確率変数の平均・分散の平行移動、定数倍に関する性質の証明
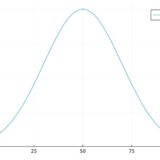
正規分布の平均、分散の求め方、証明
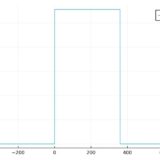
連続確率変数の平均(期待値)、分散の求め方:一様分布を例に