どうも、木村(@kimu3_slime)です。
今回は、2変数の離散同時確率分布、周辺分布とは何か、一様分布を例に紹介します。
前提知識:離散確率分布とは:一様分布、ベルヌーイ分布、二項分布、ポアソン分布を例に
2変数の離散確率分布とは
2次元の確率分布
公平なコインとサイコロをそれぞれ1回投げる状況について考えましょう。
このような問題を考えるには、2次元的な確率を考える必要があります。
コインについて起こる結果の集合は\(\Omega_1 =\{0,1\}\)、サイコロについては\(\Omega_2 =\{1,2,\dots,6\}\)で、それらをひとつに合わせれば\(\Omega =\Omega _1 \times \Omega_2\)という直積集合を考えることになります。例えば、コインが表、サイコロの目が4という結果は\((1,4)\)という順序対です。
起こりうる結果は合計で\(2\times 6=12\)通りあります。公平なコインとサイコロを考えることは、\(\Omega\)上に次のような確率測度\(P\)(一様分布)を考えることに対応するわけです。
\[P(A) = \frac{\mathrm{card}(A)}{12}\]
ただし、\(\mathrm{card}(A)\)は事象\(A \subset \Omega\)の要素の個数です。例えば、コインが表、サイコロの目が4となる確率は\(P(\{(1,4)\})= \frac{1}{12}\)となります。
このような確率測度を2次元の確率分布(two-dimensional probability distribution)と呼びます。
離散確率変数、確率質量関数
コインとサイコロを投げる試行について、変数を分けて考えるために、2つの離散確率変数\(X,Y\)を考えましょう。\(Z(\omega)=(X(\omega), Y(\omega))\)という組により決まる確率変数\(Z:\Omega \to \mathbb{R}\)を、2次元の離散確率変数(two-dimensional discrete random variable)と呼びます。
1次元の確率変数で確率質量関数を考えたように、2次元でも同じことを考えましょう。
\[f_{X,Y}(x,y) = P(X=x,Y=y)\]
により定まる2変数関数\(f_{X,Y}\)を、確率変数\((X,Y)\)の(同時)確率質量関数(pmf; probability mass function)と呼びます。確率変数が取り得ない値\((x,y)\)となる場合には、右辺は空集合の確率、つまり\(f_{X,Y}(x,y)=0\)です。
複数の確率変数や確率質量関数に対応して決まる多次元の確率測度\(P\)を、同時確率分布(joint probability distribution)と呼びます。今回の例は、2つの確率変数、確率分布を結合したものです。
コインとサイコロのケースで具体的に考えると、
\[f_{X,Y}(x,y)= \begin{cases} \frac{1}{12} & ((x,y) \in \Omega)\\0 & (それ以外)\end{cases}\]
です。
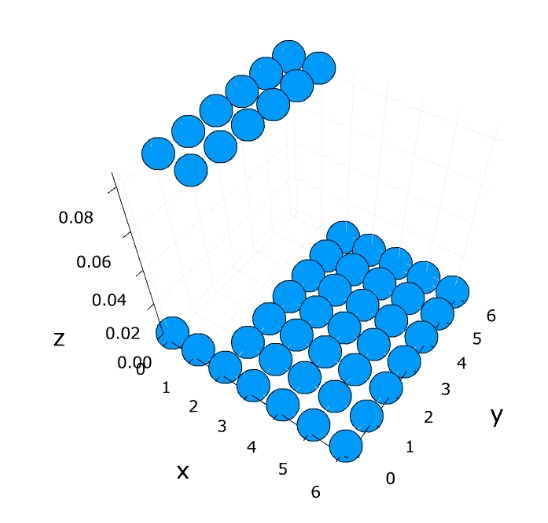
すべての事象を考えたときの確率は1なので、確率質量関数の総和は
\[\sum_{i}\sum_{j}f(x_i,y_j)=1\]
となります。
累積分布関数
1変数の場合と同様に、一定の値以下の累積した確率を求める関数
\[F_{X,Y}(x,y):= P(X \leq x, Y \leq y)\]
を(同時)累積分布関数(cdf; culminative distribution function)と呼びます。

これは確率質量関数を足し合わせていった値を取るもので、
\[F_{X,Y}(x,y) = \sum_{x_i \leq x} \sum_{y_j \leq y}f_{X,Y}(x_i,y_j)\]
という関係が成り立ちます。
一様分布の例で\(F_{X,Y}(1,4)\)を求めるならば、確率質量関数が\(2\times 4=8\)個の値を取っているので、\(F_{X,Y}(1,4)= \frac{8}{12}= \frac{2}{3}\)です。これは(コインが表または裏が出て)サイコロの目が4以下となる確率を表します。
周辺分布
2次元の確率分布について、一方の変数について条件を課さずに得る確率分布
\[P_X (A_1): = P(X \in A_X ,Y \in \mathbb{R} )\]
\[P_Y (A_2): = P(X \in \mathbb{R} ,Y \in A_2 )\]
をそれぞれ\(X,Y\)の周辺分布(marginal distribution)と呼びます。
これに対応して、
\[\begin{aligned} f_{X}(x) &= P(X=x,Y\in \mathbb{R}) \\ &= \sum_{y} f_{X,Y}(x,y)\end{aligned}\]
\[\begin{aligned} f_{Y}(y) &= P(X\in \mathbb{R},Y=y) \\ &= \sum_{x} f_{X,Y}(x,y)\end{aligned}\]
によって定まる1変数関数をそれぞれ\(X,Y\)の周辺確率質量関数(marginal probability mass function)と呼びます。
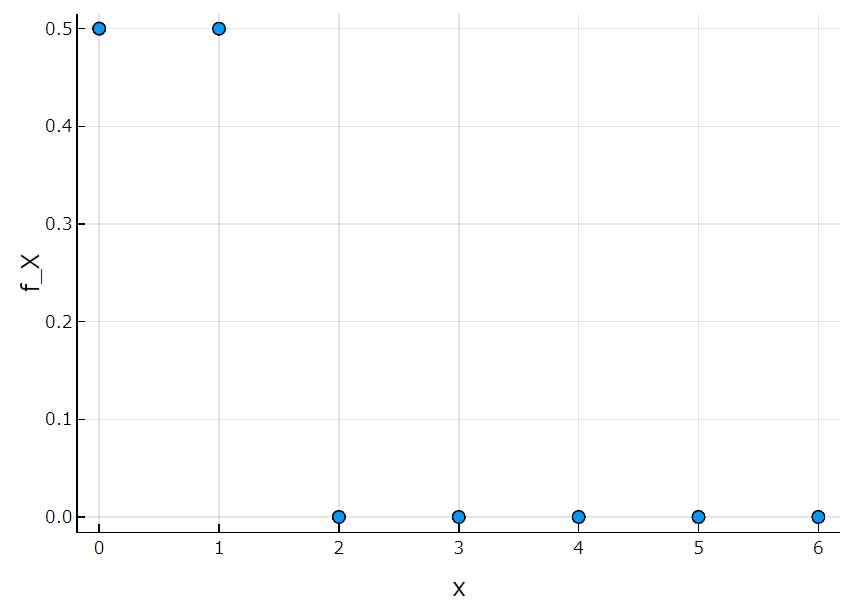
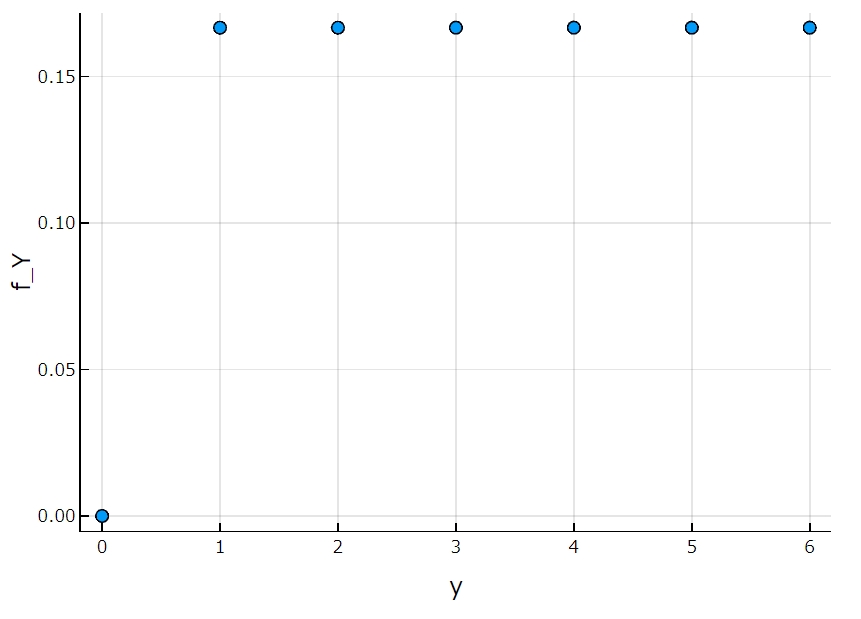
\(X\)に関する周辺確率質量関数は、\(Y\)の結果に関わらず、\(X\)が特定の値を取る確率を表します。一様分布の例ならば、\(f_X\)はコイン投げの方の確率の値、\(f_Y\)はサイコロ投げの確率の値ですね。
同様に、
\[\begin{aligned} F_{X}(x) &= P(X\leq x,Y\in \mathbb{R}) \\ &= \sum_{s \leq x} f_{X}(s)\end{aligned}\]
\[\begin{aligned} F_{Y}(y) &= P(X\in \mathbb{R},Y\leq y) \\ &= \sum_{t \leq y} f_{Y}(t)\end{aligned}\]
をそれぞれ\(X,Y\)の周辺確率質量関数(marginal probability mass function)と呼びます。
同時分布という用語では2つの変数をセットで考え、周辺分布という用語ではひとつの変数に注目し他方の結果を気にしない、という違いがありますね。
以上、2変数の離散同時確率分布、周辺分布とは何か、一様分布を例に紹介してきました。
一様分布同士の組み合わせ以外にも同時確率分布を考えることはできますが、まずは簡単な例として一様分布を知っておくと良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
離散確率分布とは:一様分布、ベルヌーイ分布、二項分布、ポアソン分布を例に