どうも、木村(@kimu3_slime)です。
今回は、離散確率分布とは:一様分布、ベルヌーイ分布、二項分布、ポアソン分布を例に紹介します。
離散確率分布とは
確率分布とは
公平なコインを投げる問題を、数学的に表してみましょう。
起こりうる結果は\(表,裏\)で、それを集めた集合\(\Omega =\{表,裏\}\)は標本空間(sample space)と呼ばれます。
確率(測度)\(P\)は、事象(標本空間の部分集合)に対して、0以上1以下の値を割り当てる関数です。
考えているコインは公平なので、例えば\(P(\{表\})= \frac{1}{2}\)、\(P(\{表,裏\})= 1\)を満たす\(P\)を考えているわけです。
コインを1回投げるという試行は、一般には確率変数(random variable)と呼ばれる関数\(X:\Omega \to \mathbb{R}\)で表されます。
表が出る回数を\(X\)とするなら、\(X(表)=1\)、\(X(裏)=0\)とすれば良いわけです。確率測度と確率変数を組み合わせると、
\[P(X=1) = \frac{1}{2}\]
\[P(X=0) = \frac{1}{2}\]
という関係が成り立っています。これはコインを1回投げて、表が出る確率は\(1/2\)、裏が出る確率は\(1/2\)という意味です。
このような確率測度と確率変数の関係性があるとき、確率測度\(P\)は確率分布(probabirity distribution)と呼び、確率変数\(X\)は確率分布に従うといい、\(X \sim P\)と書きます。
平等なコイン投げの確率測度は、どの値も同じく\(1/2\)で、一様分布と呼ばれるものです。上で定めた確率変数は、一様分布に従っていると言えます。
特に、今回考える確率分布では、\(X\)の取りうる値が離散的(有限集合や可算無限集合)です。このときは、離散確率分布、離散確率変数と呼ばれます。
確率分布と確率変数は、次のように確率関数として捉えられることが多いです。
\[f(k):= P(X = k)\]
コイン投げの例ならば、表が\(k\)回出る確率を表す関数です。実現されない\(k\)に対しては、\(f(k)=0\)と考えています。
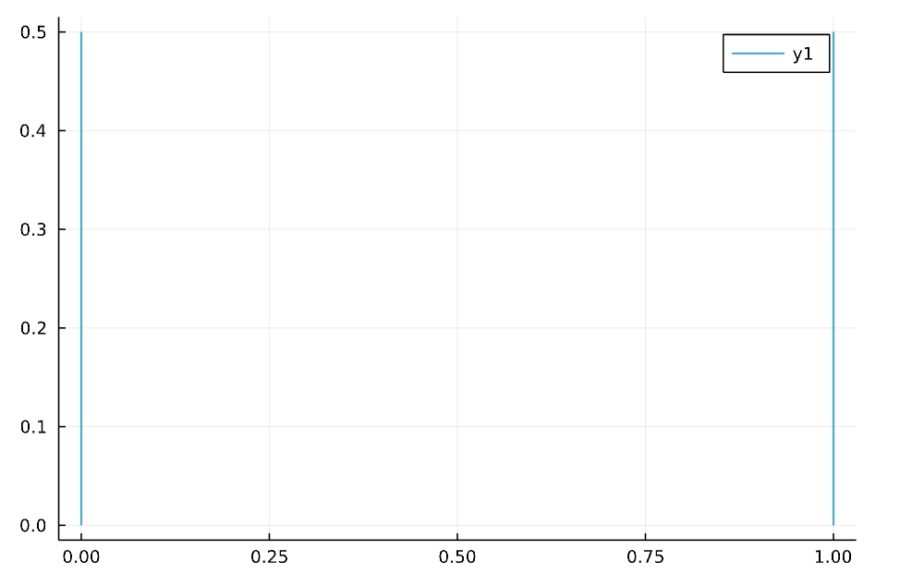
一般に、確率変数\(X\)の実現値\(k\)に対し、それが実現する確率\(P(X=k)\)を割り当てる関数\(f: \mathbb{R} \to \mathbb{R} \)を、確率質量関数(pmf; probability mass function)と呼びます。単に確率関数とも。
確率分布の説明で持ち出されるグラフは、この\(f\)であることが多いですね。
コンピュータを使った一様分布に従う乱数によって、10回、100回、1000回コイン投げをした結果の分布(ヒストグラム)は次の通り。試行回数が増えるほど、一様分布の形に近づくと予想されます。
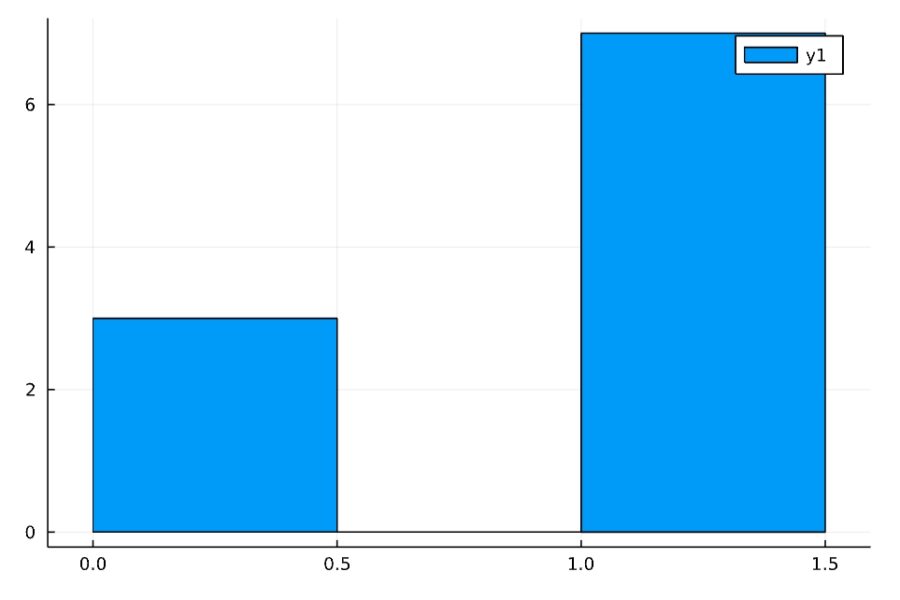
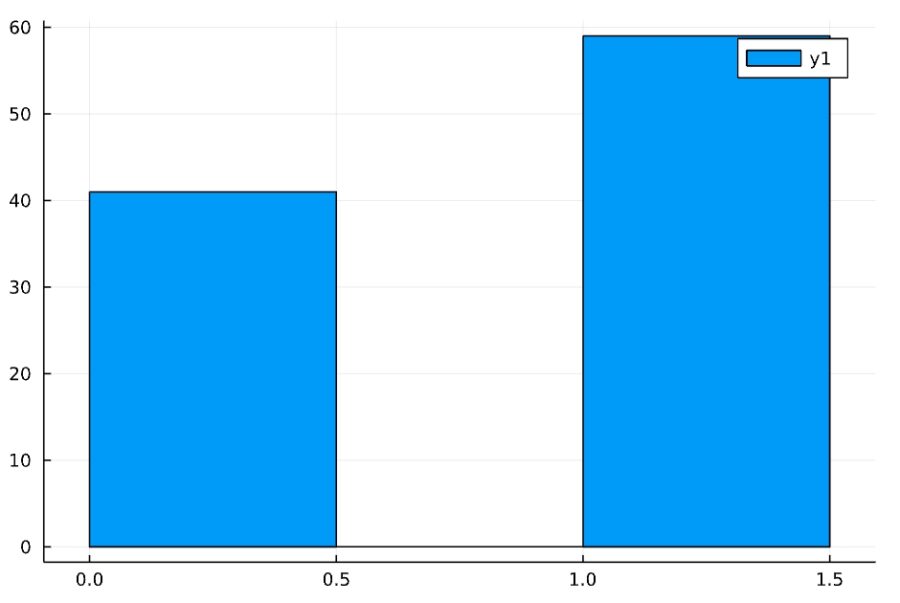
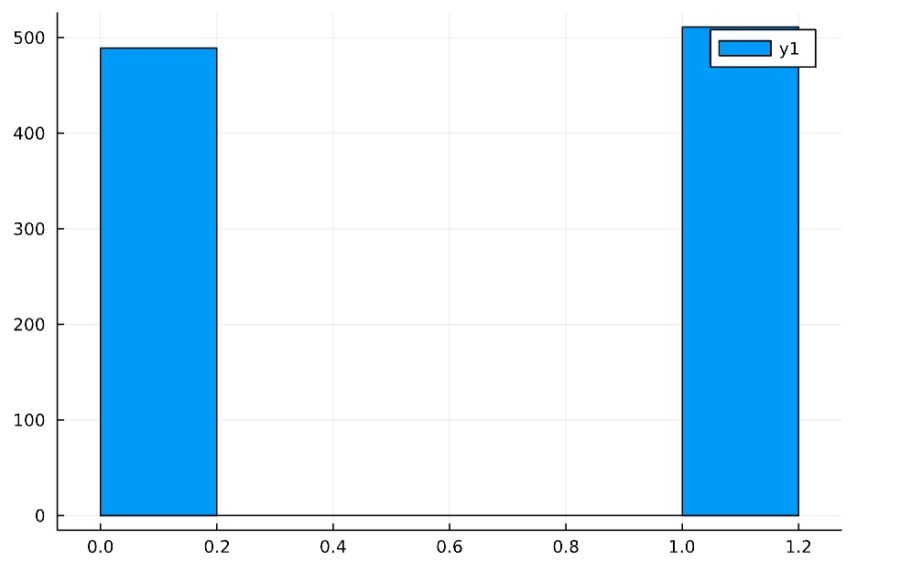
こうした繰り返しの観測に隠れている、試行回数によらない現象、理論的な物事の起こる割合:確率の形を見出すのが、確率分布の考え方です。
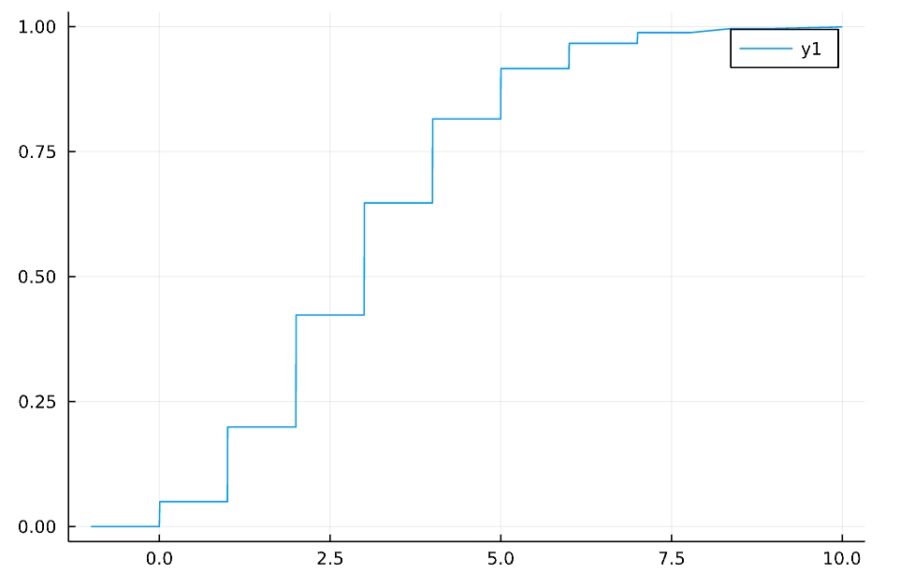
確率質量関数を足し合わせていってできる関数を、確率分布関数(cdf; cumulative distribution function)と呼びます。単に分布関数とも。
\[F(k) : = \sum_{\ell \leq k} f(\ell)\]
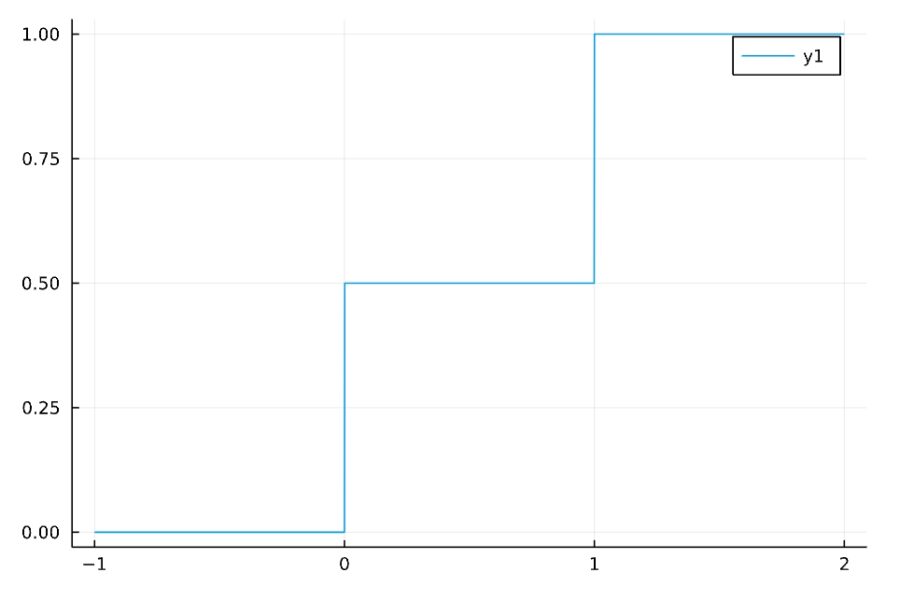
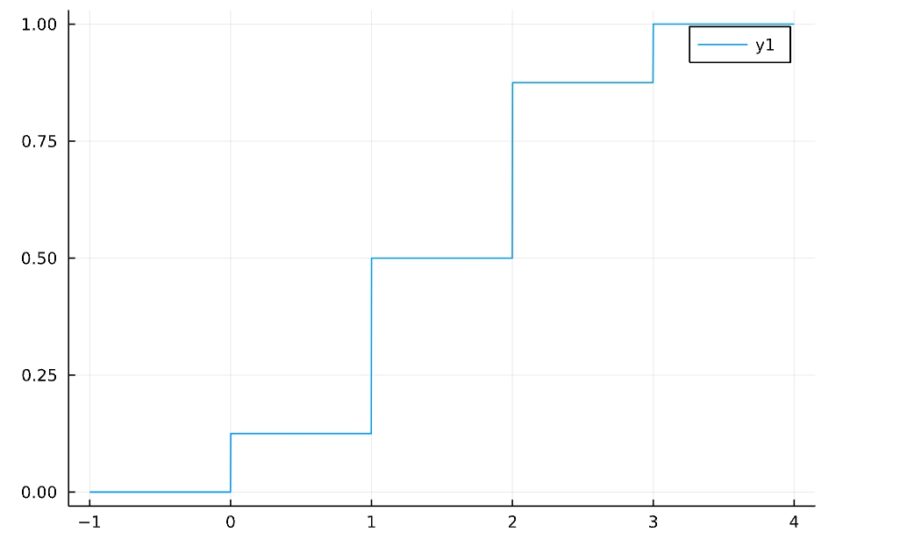
離散確率変数の確率分布関数は、確率質量関数が飛び飛びで連続でないので、階段状になります。
一様分布
では、離散確率分布の例をいくつか紹介していきましょう。
離散一様分布(discrete uniform distribution)は、最も簡単な確率分布のひとつです。
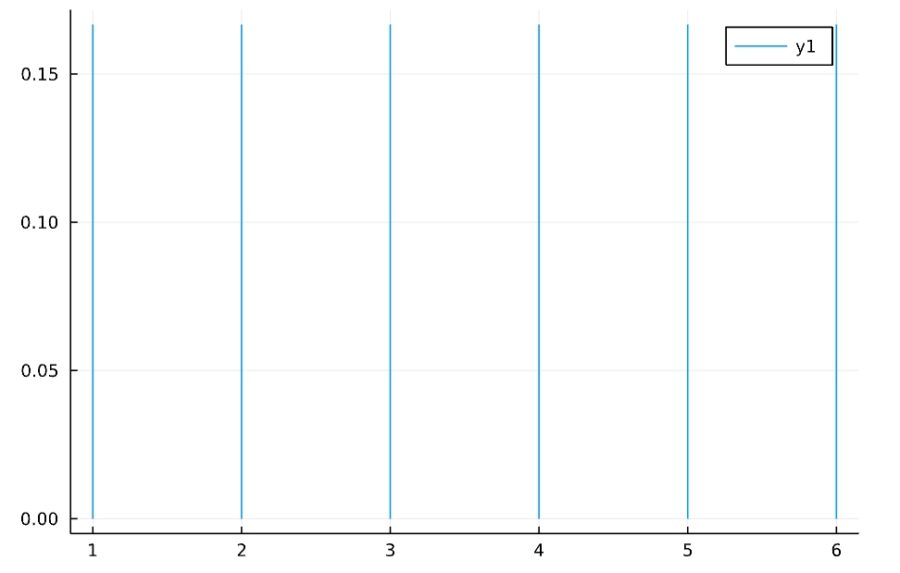
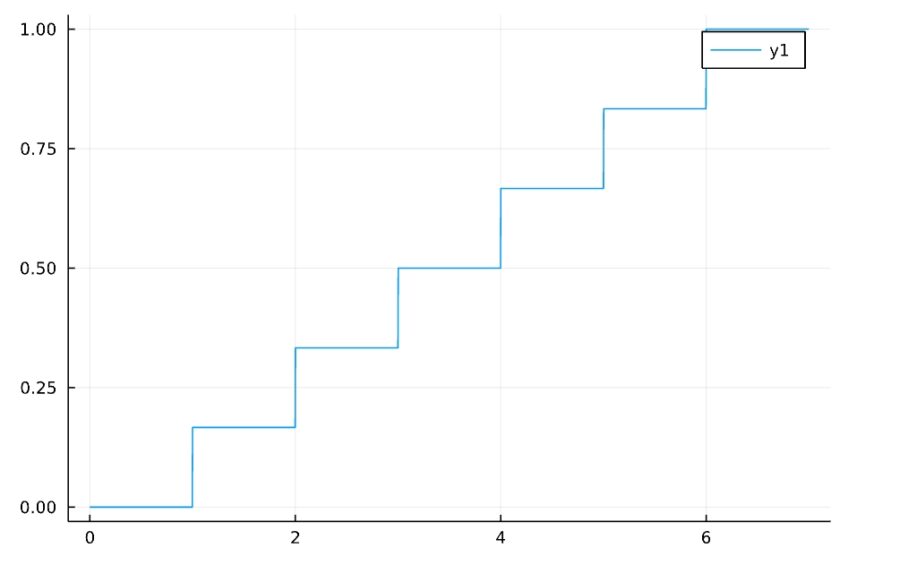
\(a\)以上\(b\)以下の離散一様分布DiscreteUniform(a,b)は、
\[P(X=k) = \frac{1}{b-a+1}\]
です。ただし、\(k=a, a+1,\dots,b\)。
公平なサイコロを投げるケースならば、\(a=1,b=6\)に対応します。確率質量関数と累積分布関数は次の通り。
ベルヌーイ分布
コインを1000回投げて、次のようなヒストグラムが得られたとしましょう。
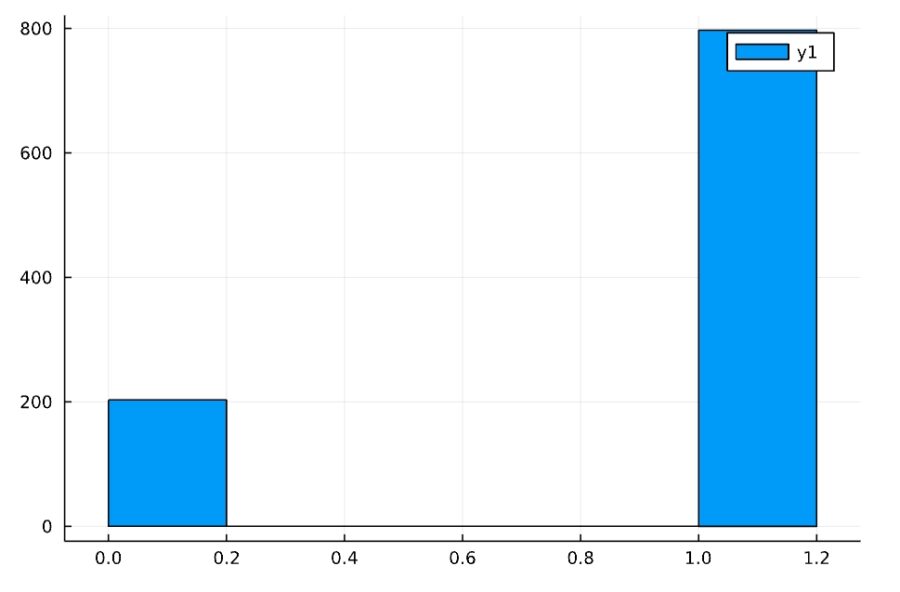
流石にこのコインが平等であるとは考えにくいですね。表と裏の出る確率の違う、いびつなコインでしょう。
ベルヌーイ分布(Bernoulli distribution)は、起こりうる結果が2種類で、その一方が確率\(p\)で起こるような分布です。
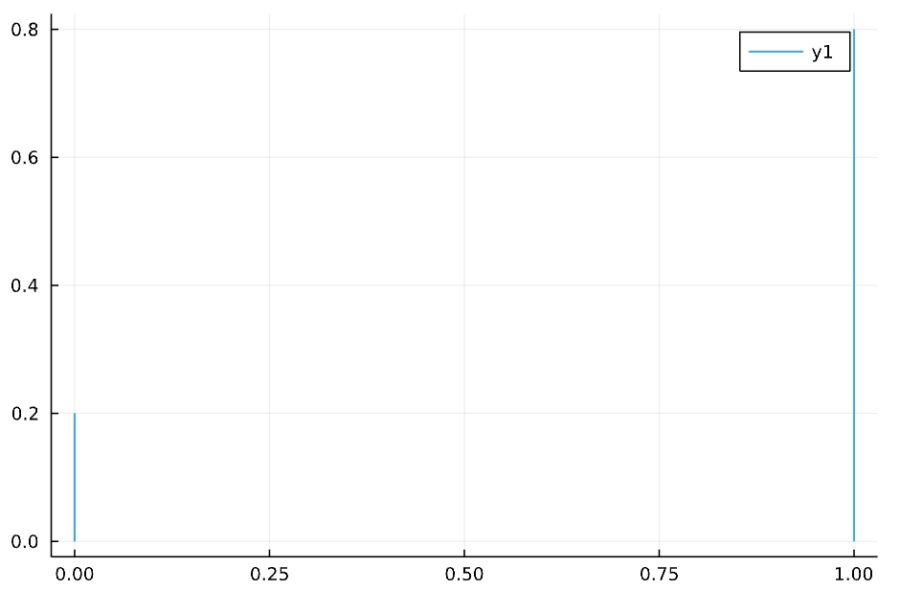
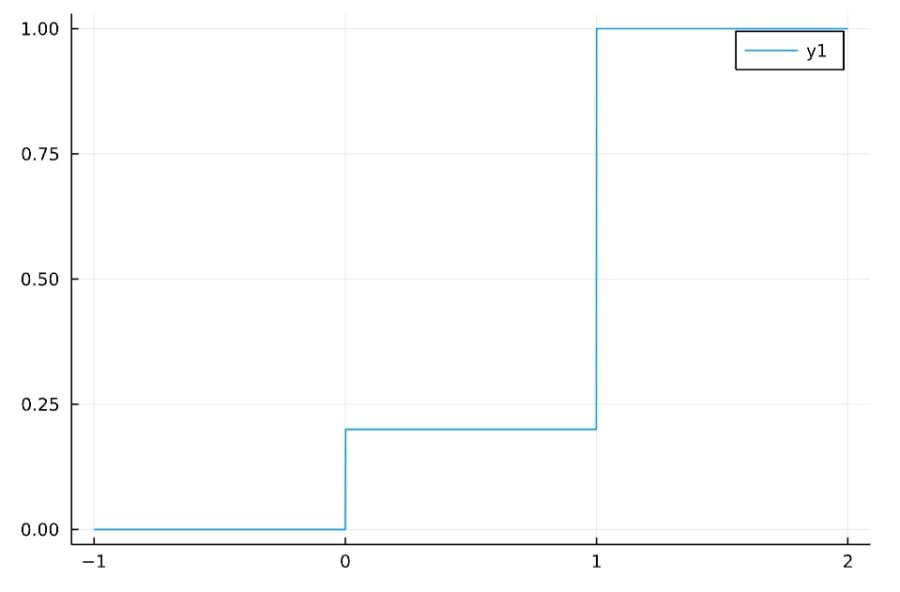
パラメータ\(p\)は、\(0\)以上\(1\)以下の実数です。Bernoulli(p)の定義は次の通り。
\[P(X=k)= \begin{cases}1-p & (k=0 )\\p & (k=1)\end{cases}\]
\(p=0.8\)のときの確率質量関数、累積分布関数は次の通り。
二項分布
「コインを3回投げて表が出た回数」を1000回観測してヒストグラムにすると、次のようになりました。
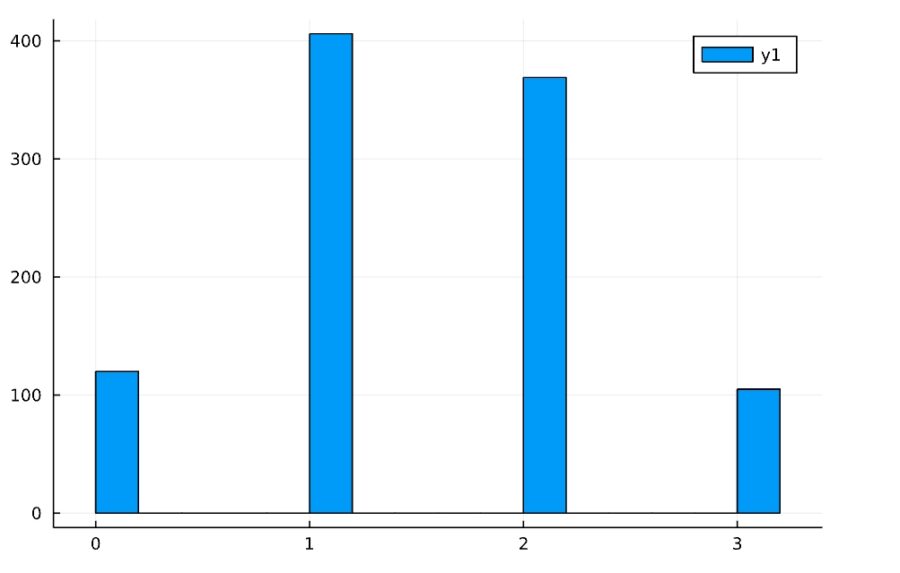
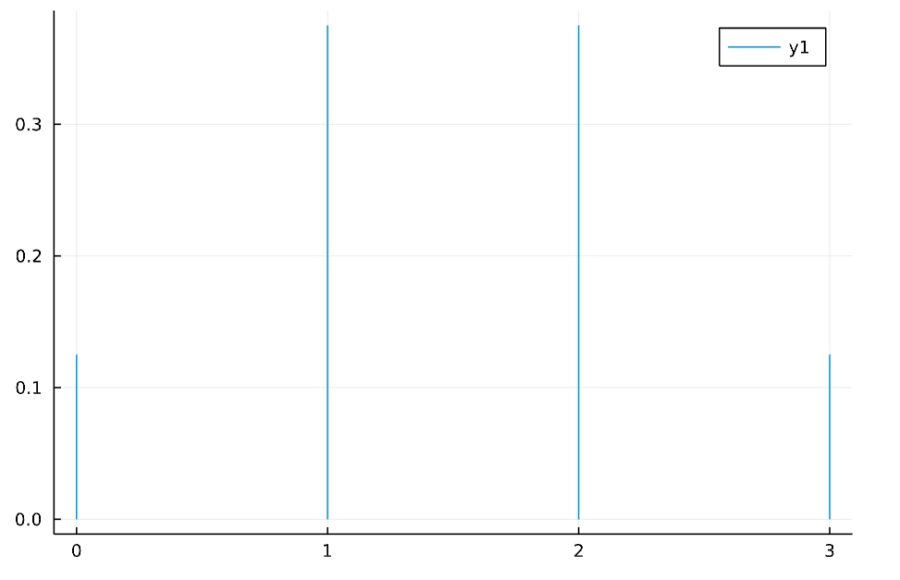
結果が2通りしかない試行(ベルヌーイ試行)を\(n\)回繰り返して、成功する回数を\(X\)とするとき、それが従う分布は二項分布(binomial distribution)と呼ばれます。
一般形Binomial(n,p)は、次のように定義されます。nが試行回数、pが一方が起こる確率です。
\[P(X=k) =C(n,k) p^k (1-p)^{n-k}\]
ただし、\(C(n,k)\)は二項係数です。1回目の表裏、2回目の表裏……などの結果を組み合わせた計算ですね。
\(n=3,p=0.5\)のときの確率質量関数、累積分布関数は次の通り。
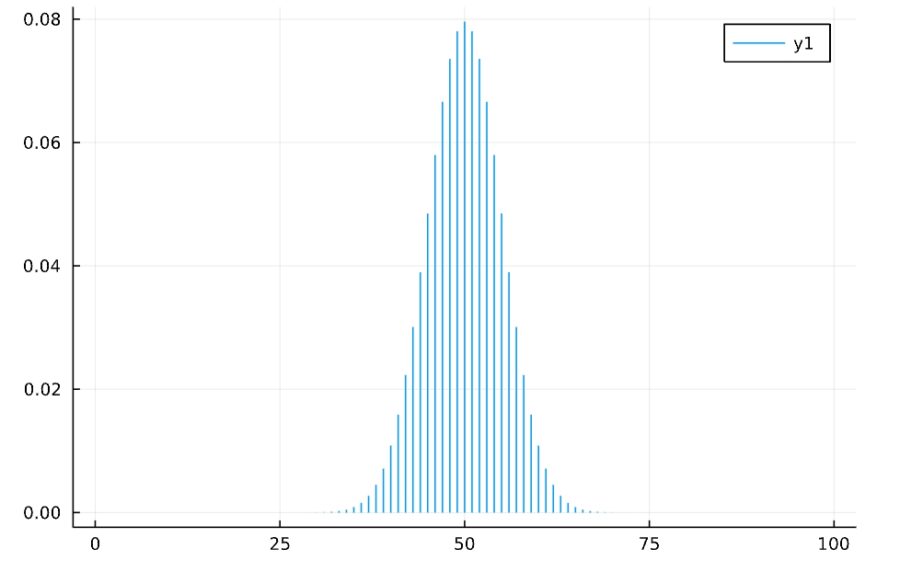
二項分布において、試行回数\(n\)を大きくすると、正規分布という重要な連続確率分布に近づくことが知られています。
ポアソン分布
ある工場で1000個のネジを作ったとき、不良品の個数が次のような形のヒストグラムになったとしましょう。
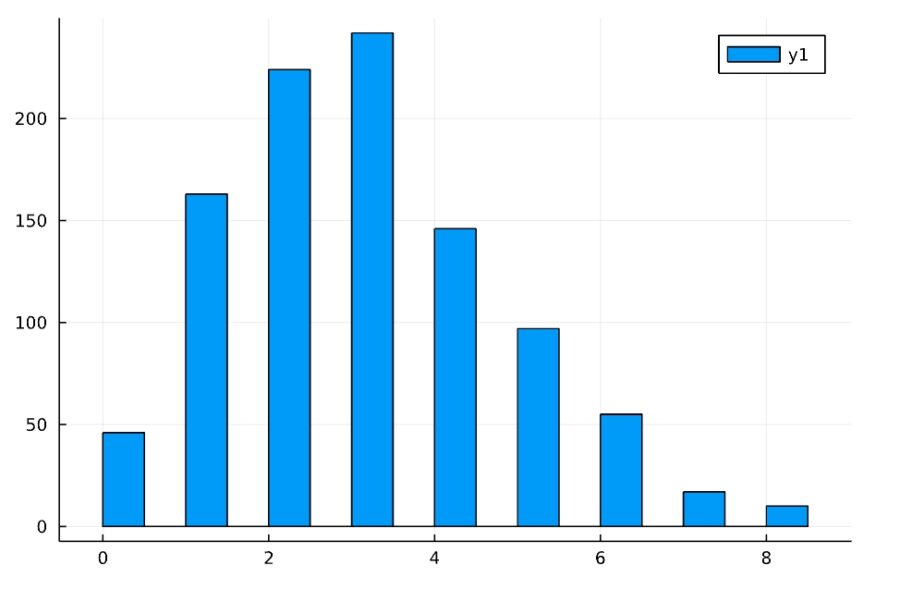
不良品や事故など、滅多に起こらない確率の低い現象が起こる回数は、ポアソン分布(Poisson distribution)によって説明されます。
パラメータ\(\lambda\)は平均で起こる割合として、Poisson(λ)は次のような定義です。
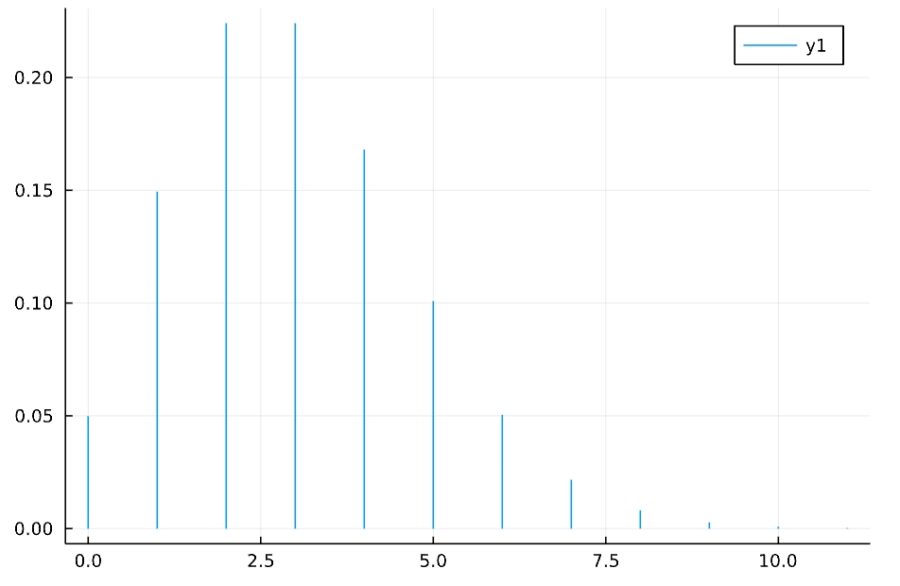
\[P(X=k) = \frac{\lambda ^k}{k!}e^{-\lambda}\]
階乗の効果によって、\(k\)が大きくなると確率が急速に小さくなることがわかりますね。
\(\lambda =3\)のときの確率質量関数、累積分布関数は次の通り。
以上、離散確率分布とは何か、一様分布、ベルヌーイ分布、二項分布、ポアソン分布を例に紹介してきました。
確率分布まわりの用語は慣れるまで難しいので、一様分布やベルヌーイ分布のような簡単な例から考え、想定する現象と数式とグラフの関係を理解すると良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
無限集合の濃度とは? 写像の全単射、可算無限、カントールの対角線論法