どうも、木村(@kimu3_slime)です。
今回は、連続確率分布とは何か:一様分布、正規分布を例に例に紹介します。
連続確率分布とは
確率分布とは
確率分布の考え方は、離散確率変数の記事で紹介しました。
そこでは確率変数の取りうる値が離散的でした。コインを1回投げるとき表が出る回数は\(\{0,1\}\)、サイコロを1回投げるときは\(= \{1,\dots,6\}\)、不良品が発生する回数は\(\{1,2,\dots\} =\{ k \in \mathbb{Z} \mid k \geq 0\}\)などとなりました。これらは有限集合、または可算無限集合で、離散的(飛び飛びの値を取る)です。
一方、確率的に起こる現象は、飛び飛びの値を取るとは限りません。例えば、コマを回して倒れたときの角度、生き物の体長、重さ、温度などは連続的な値=実数値を取ります。
計測値として\(1.4\)が得られたとしても、それには必ず誤差が伴い、精度を上げればより細かな値が得られるでしょう。観測値\(X\)がちょうど\(1.4\)を取る確率\(P(X=1.4)\)ではなく、観測値が\(1.4\)以上\(1.5\)以下である確率\(P(1.4 \leq X \leq 1.5)\)を求めたくなります。したがって、実数の部分集合に対して確率を割り当てる、連続的なものを考えると便利です。
標本空間が実数全体\(\mathbb{R}\)であるとき確率測度\(P\)は連続確率分布(continuous probability distribution)、取りうる値(定義域全体の像)が連続的(実数の非可算部分集合)であるとき確率変数\(X:\Omega \to \mathbb{R}\)は連続確率変数(continuous random variable)と呼ばれます。
連続確率分布の例としては、一様分布、正規分布などがあり、具体的には後で紹介しましょう。
連続確率分布\(P\)は、一般的には次のようにして定義されます。確率変数\(X\)が値\(x\)以下を取る事象を\(X \leq x :=\{\omega \in \Omega \mid X(\omega) \leq x\}\)と表すとき、
\[P(X \leq x)\]
を各\(x\)に対して定めれば良いです。これを\(x\)の関数として見るとき、
\[F(x) = P(X \leq x)\]
を累積分布関数(cdf; cumulative distribution function)と呼びます。累積分布関数は、ある関数\(f\)の積分として定義することが多いです。
\[F(x)=\int _{-\infty} ^x f(s)ds\]
その値は、\(X\)が\(x\)以下の値を取る確率を表し、それは\(f\)のグラフの面積に等しいです。
\(f\)は確率の密集具合を表す関数で、確率密度関数(pdf; probability density function)と呼ばれます。微積分学の基本定理から、\(f(x)= F^{\prime}(x)\)という関係性があります。
数学的な議論の順序としては、確率分布と確率変数が先にあるわけですが、感覚的な説明としては確率密度関数から入るのがわかりやすいです。具体的に見ていきましょう。
一様分布
コマを回して倒れて止まったときの角度を500回測り、次のようなヒストグラムができたとします。
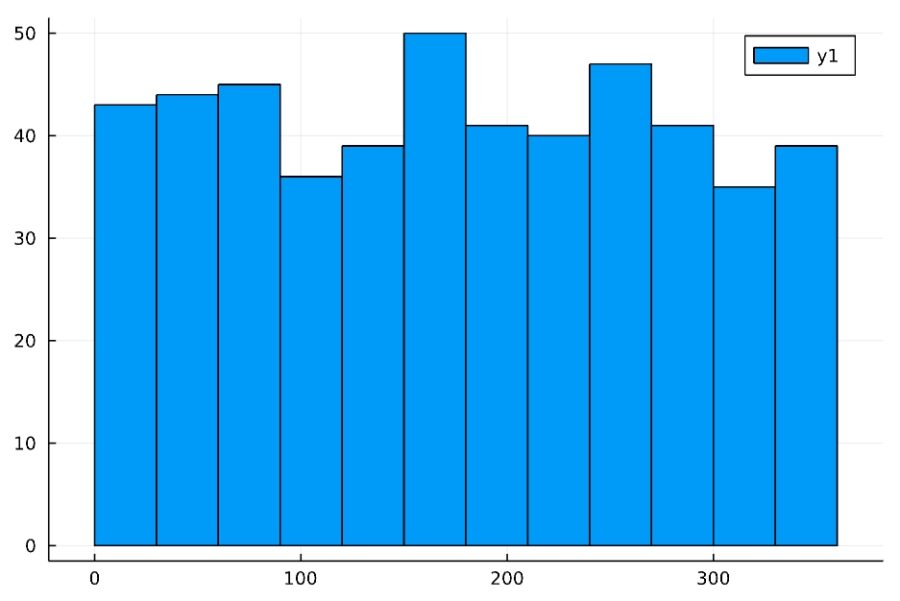
投げ方や地形にクセがなければ(公平ならば)、どの方向にも同じように倒れる可能性があり、倒れる角度は同じような確率でしょう。
このように確率が一様である確率分布を、連続一様分布(continuous uniform distribution)と呼びます。サイコロの目が1から6まで出る確率は等しく\(1/6\)ですが、それを連続的に一般化したものと言えるでしょう。
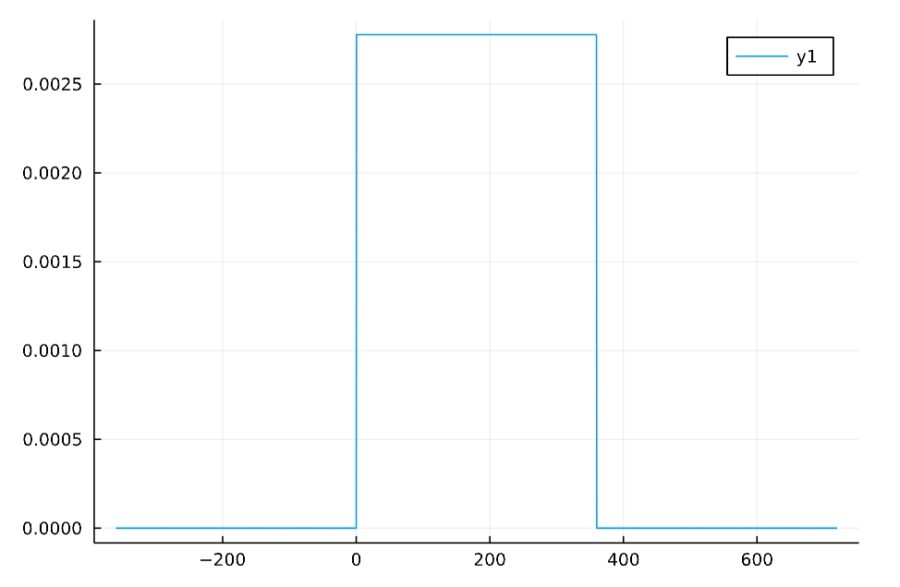
取りうる値の下限を\(a\)、上限を\(b\)として、一様分布Uniform(a,b)の確率密度関数は
\[f(x)= \begin{cases} \frac{1}{b-a} & (a <x <b )\\0 & (それ以外)\end{cases}\]
と定義されます。
\(a=0,b=360\)のときの確率密度関数のグラフは次の通り。
累積分布関数は、さきほどの定義の仕方から、\(a<x<b\)のときは、
\[\begin{aligned} F(x) &= P(X \leq x) \\&= \int_{a}^x \frac{1}{b-a}ds \\&= \frac{x-a}{b-a} \end{aligned}\]
となります。
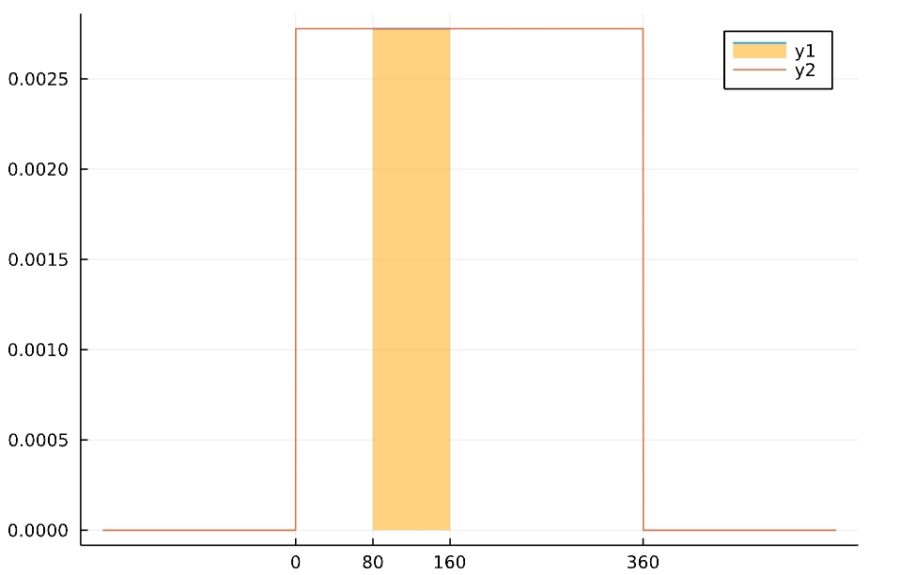
例えば、\(a=0,b=360\)で、観測値が\(80 \leq X \leq 160\)となる確率は、
\[\begin{aligned} P(80 \leq X \leq 160) &= F(160)-F(80) \\ &= \int_{80}^{160} \frac{1}{360}ds \\ &= \frac{160-80}{360} \\&= \frac{2}{9}\end{aligned}\]
となります。この確率の計算は、確率密度関数のグラフの面積を求めることに対応するものです。
離散確率分布との違いとして、連続確率分布では、確率変数が特定の「値」を取る確率は0です。
\[P(X= 200)=0\]
ピタリと200度になる確率は、0に等しいのです。もし200度に近く倒れる確率を求めたいならば、\(199.5 \leq X \leq 200.5\)といった区間の確率を求めることになるでしょう。したがって、区間の確率は、
\[P(a < X \leq b) = P(a \leq X \leq b) = P(a< X <b)\]
と、端点を含もうが含むまいが変わりません。1点の長さは「0」として扱われ、区間の長さのみが影響するのです。
累積分布関数のグラフは次の通り。
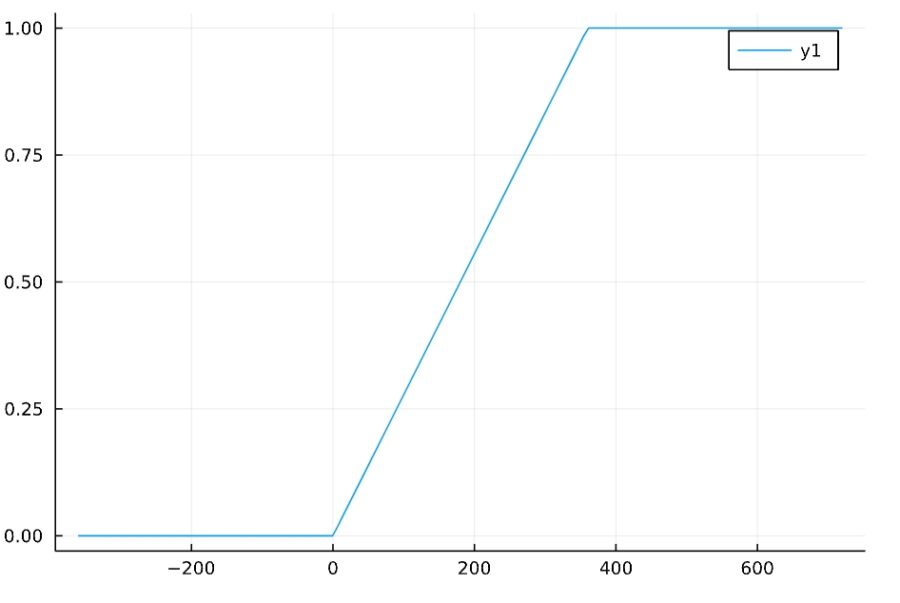
直線的に、一様なペースで確率の累積値は増加していきます。
正規分布
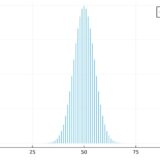
あるクラスのテストの成績が、次のようなヒストグラムであったとしましょう。
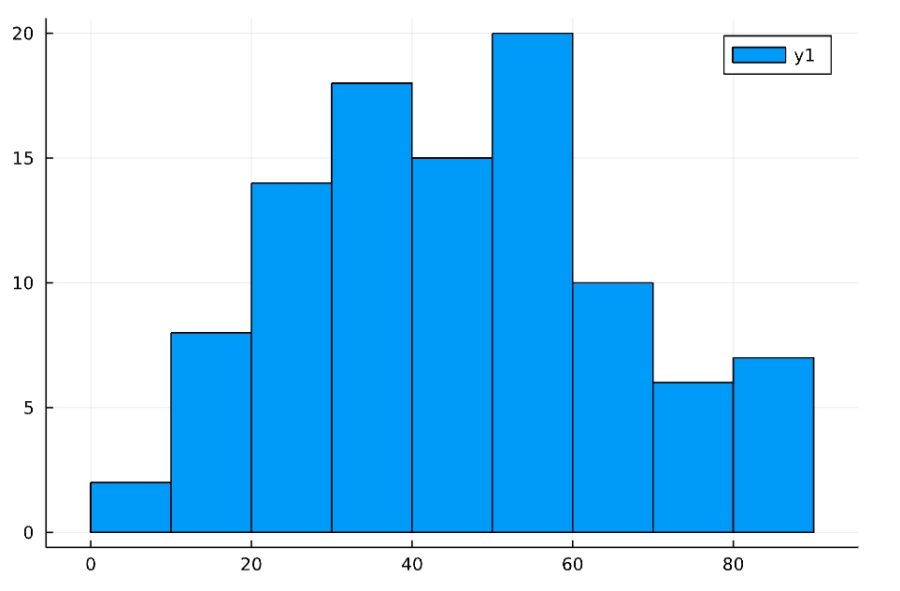
テストの点数や、生物の身長や体重など、平均値を取るデータが多い分布は、正規分布(normal distribution)で近似できることが多いです。ガウス分布(Gaussian distribution)とも。
平均\(\mu\)、標準偏差\(\sigma\)(分散\(\sigma ^2\))の正規分布Normal(μ,σ)の確率密度関数は、次のように定義されます。
\[f(x) = \frac{1}{\sqrt{2\pi \sigma ^2} } \exp(-\frac{(x-\mu)^2}{2 \sigma^2})\]
\(\exp(x)\)は指数関数\(e^x\)のことです。この形の指数関数は、ガウス関数(Gaussian function)とも呼ばれます。
\(\mu =50, \sigma =20\)のときの確率密度関数のグラフは次の通り。平均値付近が最も多く、そこを軸として対象です。釣鐘型の曲線、ベルカーブ(bell curve)と呼ばれる形です。
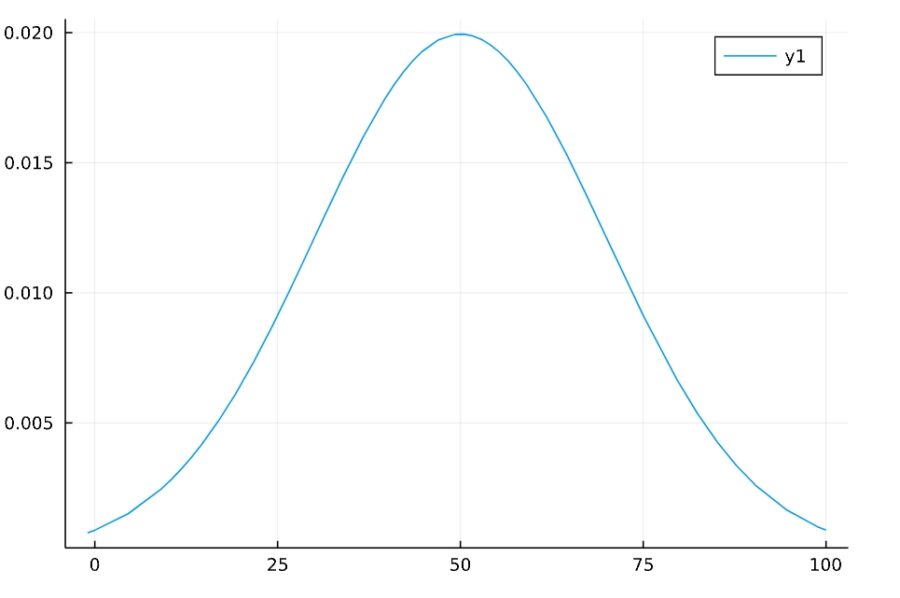
標準偏差\(\sigma\)が小さいと山は尖り、大きいと裾野が広がる形になります。
累積分布関数は、
\[\begin{aligned} F(x) &= P(X \leq x) \\&= \int_{-\infty}^x \frac{1}{\sqrt{2\pi \sigma ^2} } \exp(-\frac{(s-\mu)^2}{2 \sigma^2})ds \end{aligned}\]
です。これはガウス積分の一部で、誤差関数と呼ばれます。
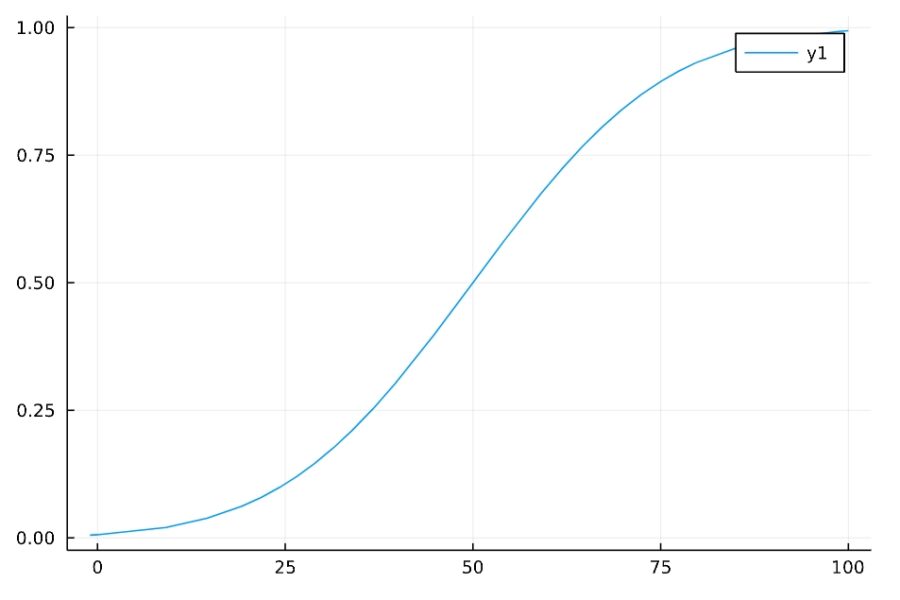
この積分は初等関数で表せないことが知られていて、数値的な計算か、計算結果を並べた正規分布表を使った計算で求めることになるでしょう。
とはいえ、個別の計算は面倒です。正規分布に従う確率変数が、特定の値の範囲を取る確率として、次の値を知っておくと便利でしょう。
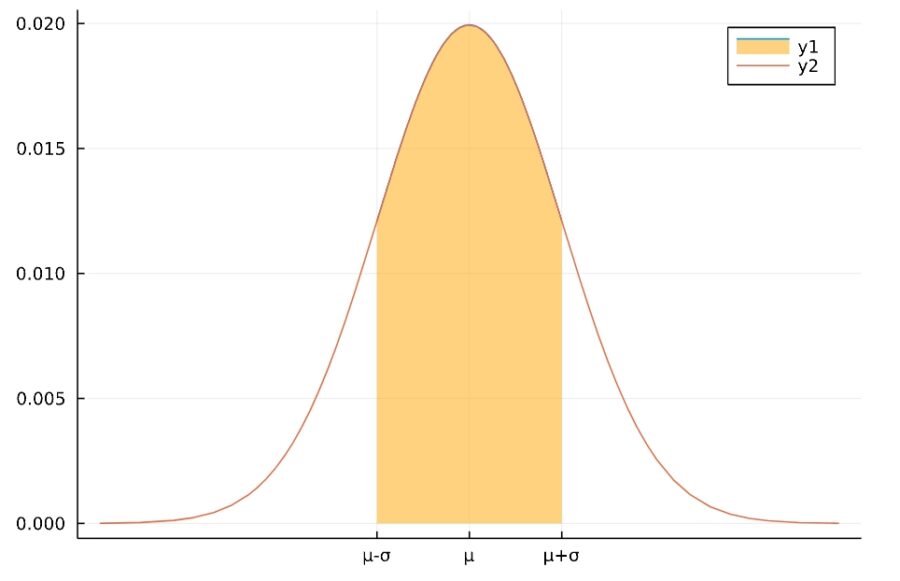
\[P(\mu-\sigma \leq X \leq \mu +\sigma) \simeq 68\%\]
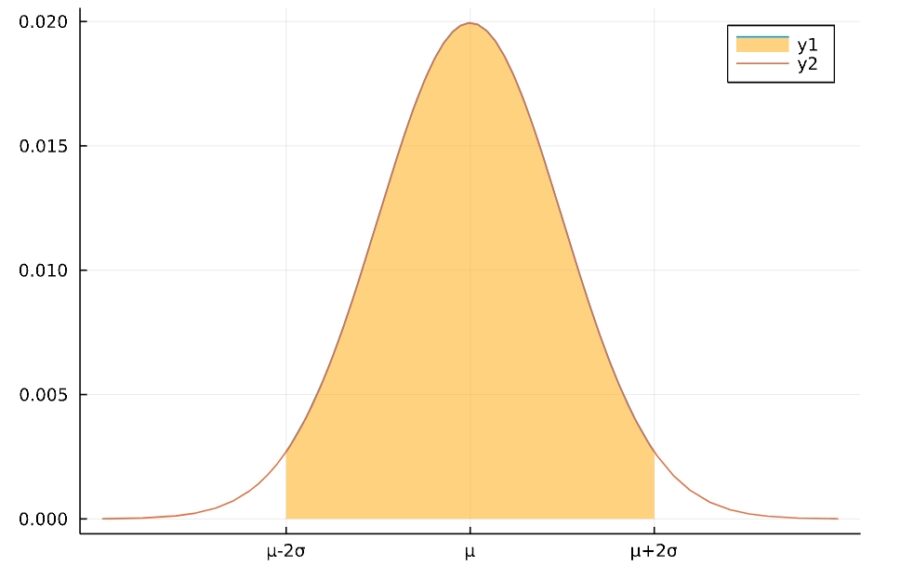
\[P(\mu-2\sigma \leq X \leq \mu +2\sigma) \simeq 95\%\]
\[P(\mu-3\sigma \leq X \leq \mu +3\sigma) \simeq 99.7\%\]
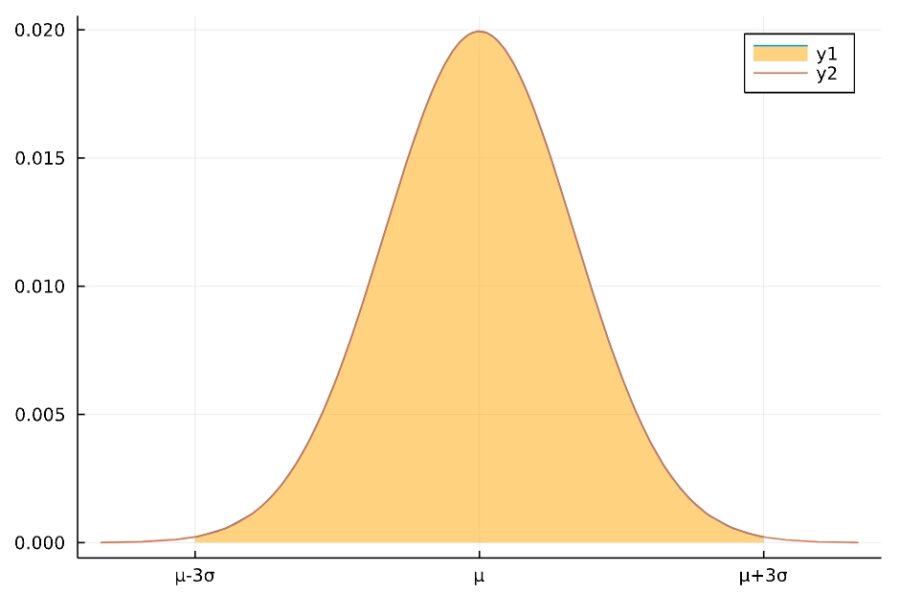
平均から\(1\sigma\)の区間には全体の\(2/3\)、\(2\sigma\)の区間には\(95\%\)、\(3\sigma\)の区間にはほぼ全体が含まれています。
この事実は、平均\(\mu\)、標準偏差\(\sigma\)によらずに一定です。例えば、正規分布に従う現象を見たら、観測値が平均から\(1\sigma\)の範囲に収まらない確率は\(1/3\)と考えられ、およその見積もりに便利です。
特に、\(\mu =0, \sigma =1\)のときの正規分布Normal(0,1)は、標準正規分布(standard normal distribution)と呼ばれています。
\[f(z) = \frac{1}{\sqrt{2\pi } } \exp(-\frac{z^2}{2 })\]
標準正規分布については、変数を\(z\)、確率変数を\(Z\)と慣習的に表すことが多いです。
一般的な正規分布Normal(μ,σ)に従う確率変数\(X\)があるとき、\(Z= \frac{X – \mu}{\sigma}\)と変換すると、\(Z\)は標準正規分布に従います(正規分布の標準化 standardization)。
一般的な正規分布の累積分布関数の計算は、この変換によって、標準正規分布について計算すれば良いことになります。したがって、教科書に掲載される正規分布表は、標準正規分布に関するものでしょう(各\(\sigma ,\mu\)について表を作ったら、切りがない)。
正規分布は、統計学において最も重要な分布です。それは、
- 二項分布の\(n\to \infty\)での極限、連続バージョンが正規分布であること(ドモアブル・ラプラスの定理)
- 母集団の分布にかかわらず、サンプルの平均と母集団の平均の差(誤差)が従う分布は、\(n\to \infty\)で正規分布に近づく(中心極限定理)。
が主な理由でしょう。
以上、連続確率分布とは何か、一様分布、正規分布を例に紹介してきました。
正規分布は非常に重要な確率分布ですが、その扱いは最初のうちは難しいかもしれません。一様分布のような簡単な例や、離散確率分布を通じて、分布の考え方や計算に慣れると良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
離散確率分布とは:一様分布、ベルヌーイ分布、二項分布、ポアソン分布を例に
無限集合の濃度とは? 写像の全単射、可算無限、カントールの対角線論法