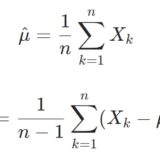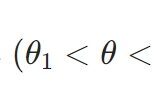どうも、木村(@kimu3_slime)です。
今回は、最尤推定法、尤度とは何か、ベルヌーイ分布を例に紹介します。
最尤推定法とは
最尤推定は、統計モデルにおけるパラメータを特定の数として推定する点推定の一種です。
母集団の分布がパラメータ\(\theta\)を持ち、その確率変数を\(X\)としましょう。\(X\)について\(n\)個のランダムサンプリングがされた(独立同分布の確率変数族\(X_1,\dots,X_n\)がある)とします。このとき、同時確率(質量・密度)関数\(f\)は、それぞれの確率関数の積として
\[f(x_1,\dots,x_n,\theta)= f(x_1 ,\theta) \cdots f(x_n ,\theta)\]
と積の形で表されます。\(X\)やサンプルは\(\theta\)に依存して決まるので、それを明示しました。そして、この関数
\[L(x_1,\dots,x_n,\theta):=f(x_1 ,\theta) \cdots f(x_n ,\theta)\]
を尤度関数(likelihood function)と呼びます。尤度関数は、パラメータ\(\theta\)のときにデータ\(x_1,\dots,x_n\)が得られる確率(密度)=起こりやすさ(もっともらしさ)を表すものです。
そして、与えられたデータ\(x_1,\dots,x_n\)に対し、尤度関数を\(\theta\)の関数として最大化するようなパラメータを推定値\(\hat{\theta}\)とする方法を、最尤推定(MLE; maximum likelihood estimation)と呼びます。
尤度は確率(密度)を表す言葉であり、推定量が「もっともらしい」ことを意味しているわけではないことに注意しましょう。最尤推定量は結果として望ましい性質を持つことが多いですが、ここでの「尤もらしさ」はそのデータが得られる確率(密度)を意味しています。
また、尤度はパラメータが\(\theta\)である確率(?)を意味するものでもありません。したがって、最尤推定は、パラメータが\(\theta\)である確率を最大化するものでもありません。最も起きやすい現象が起きる場合を尤度として高く評価し、そのときのパラメータを推定量とする方法です。
ベルヌーイ分布での例
より具体的に考えていきましょう。
あるコインを\(n\)回投げてみると、どうやら表と裏の出る回数が偏っているようです。このコインで表が出る確率\(p\)を、最尤推定してみましょう。
コイン投げは2値的な試行であり、表の出る確率を表すパラメータ\(p\)のベルヌーイ分布\(\mathrm{Bernoulli}(p)\)に従います。そして、それを\(n\)回繰り返すとき、表の出る回数は二項分布\(\mathrm{Binomial}(n,p)\)に従います。それぞれの確率質量関数は、
\[f(x_k,p)= p^{x_k}(1-p)^{1-x_k}\]
です。したがって、尤度関数は
\[L(x_1,\dots,x_n,p)= p^{x_1}(1-p)^{1- x_1} \cdots p^{x_n}(1-p)^{1-x_n}\]
となります。
尤度関数を最大化することは、対数関数を取った対数尤度関数(log-likelihood function)\(\log L(x_1,\dots,x_n,p)\)を最大化することと同値です。対数関数は単調増加なので。\(L\)が正値でときに対数が使えることに注意しましょう。
対数の性質を使えば積を和として分解することができ、
\[\begin{aligned} \log L = \sum_{k=1}^n (x_k \log p +(1-x_k)\log(1-p)) \end{aligned}\]
です。
\(p=0,1\)のときは尤度関数が恒等的に0になるので、最大にはなりません。以降では、\(p \neq 0,1\)としましょう。
関数を最大化するには、微分が有効です。最大点(極値点)ならば微分係数が0となる、パラメータ\(\theta\)に関する偏微分が0になる点
\[\frac{\partial }{\partial \theta}\log L(x_1,\dots,x_n,\theta)=0\]
を探しましょう。これは尤度方程式(likelihood equation)と呼ばれています。
ベルヌーイ分布の場合で考えると、微分の線形性より
\[\begin{aligned} \quad&\frac{\partial }{\partial p}\log L \\&= \sum_{k=1}^n (x_k \frac{1}{p} -(1-x_k)\frac{1}{1-p}) \\&=\sum_{k=1}^n (\frac{x_k}{p(1-p)}-\frac{1}{1-p}) \end{aligned}\]
となるので、微分が0となる点\(\hat{p}\)は、
\[\sum_{k=1}^n x_k \frac{1}{\hat{p}(1-\hat{p})} = \sum_{k=1}^n \frac{1}{1-\hat{p}}\]
\[\sum_{k=1}^n x_k \frac{1}{\hat{p}} = n\]
\[\hat{p}= \frac{1}{n}\sum_{k=1}^n x_k \]
と求められました。これはサンプル平均ですね。
2回微分をすると、
\[\begin{aligned} \quad&\frac{\partial^2 }{\partial p^2}\log L \\&= \sum_{k=1}^n (-x_k \frac{1}{p^2} -(1-x_k)\frac{1}{(1-p)^2}) \\&=\sum_{k=1}^n( x_k \frac{2p-1}{p^2(1-p)^2 }-\frac{1}{(1-p)^2})\\ &=n\hat{p}\frac{2p-1}{p^2(1-p)^2 } -\frac{n}{(1-p)^2}\end{aligned}\]
となるので、\(p=\hat{p}\)のとき
\[\begin{aligned} \quad&\frac{\partial^2 }{\partial p^2}\log L \\&=\frac{n\hat{p}}{p^2(1-p)^2 } (2\hat{p}-1-\hat{p})\\ &=\frac{n\hat{p}}{p^2(1-p)^2 } (\hat{p}-1) \\ &<0 \end{aligned}\]
となります。\(\hat{p} \neq 1\)に注意。
よって、1回微分が0、2回微分が負なので、
\[\hat{p}= \frac{1}{n}\sum_{k=1}^n x_k \]
が尤度関数の最大点であること、すなわち最尤推定量であることがわかりました。
コンピュータ(Julia)で、ベルヌーイ分布のパラメータの推定をしてみましょう。\(p=0.8\)を与え、それをランダムなデータから推測します。
1 2 3 4 5 6 7 8 9 10 11 12 | using Distributions,Random d = Bernoulli(0.8) k = 20 MLE = zeros(k) for i in 1:k x = rand(d,10) MLE[i] = mean(x) end println(MLE) println(count(i->(i==0.8),MLE)/k) println(mean(MLE)) |
1 2 | [0.7, 0.7, 0.8, 0.9, 0.9, 0.8, 0.9, 0.8, 0.7, 0.8, 0.7, 0.8, 0.7, 1.0, 0.9, 0.9, 0.6, 0.9, 0.9, 0.8] 0.8099999999999999 |
「10個のサンプルから最尤推定量を計算する」という流れを、20回行っています。
サンプル平均は不偏推定量でもあるので、この推定量の平均は\(0.8\)に近づいていますね。
k=10000のときの推定値の平均、分散とヒストグラムは
1 2 3 4 5 6 7 8 9 | using StatsPlots k =10000 MLE = zeros(k) for i in 1:k x = rand(d,10) MLE[i] = mean(x) end println(mean(MLE)) display(histogram(MLE)) |
1 2 | 0.8014999999999998 0.015789328932893285 |
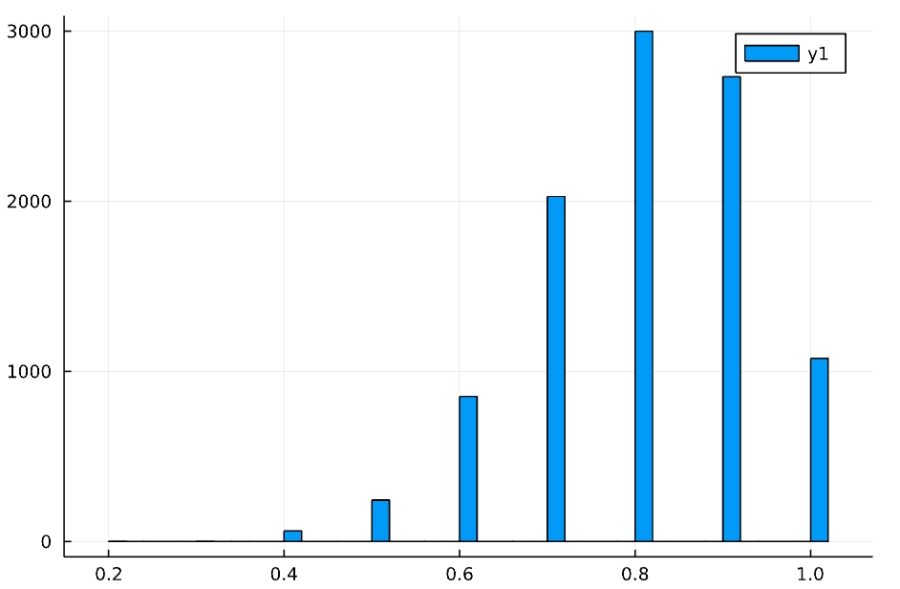
となります。10個のサンプルからの調査ですが、\(0.8\)に近い値が推定されてることが多いですね。
以上、最尤推定法、尤度とは何か、ベルヌーイ分布を例に紹介してきました。
今回はパラメータ1つで考えましたが、複数のパラメータを持つケースならば、複数の偏微分を考えることで最尤推定量を考えられます。
ただし微分によって求められるのは尤度関数の微分可能性があるおかげで、最尤推定量が存在しないような例もあります。
最尤推定法によっていつでも簡単に推定量を求められるとは限りませんが、多くのケースで通用する一般的な点推定の方法として知っておくと良いでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
Probability and Statistics: Pearson New International Edition
Pearson Education Limited (2013-07-30T00:00:01Z)
¥10,792 (中古品)
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)
こちらもおすすめ
点推定、不偏推定量とは:平均と分散を例に、なぜn-1で割るのか
連続関数、可積分関数の線形空間(関数空間)、微分と積分の線形性とは