正規分布の平均、分散の求め方、証明

どうも、木村（@kimu3_slime）です。

今回は、正規分布の平均、分散の求め方、証明を紹介します。

前提知識：連続確率変数の平均（期待値）、分散の求め方：一様分布を例に

正規分布の平均、分散の求め方

連続確率変数\(X\)の平均、分散の定義をおさらいしておきましょう。\(f\)を\(X\)の確率密度関数とするとき、

\(X\)の平均（mean）、または期待値（expected value）は

\[E(X):= \int_{-\infty}^\infty x f(x)dx\]

で、分散（variance）には

\[\begin{aligned} V(X) &:= \int_{-\infty}^\infty (x-E(X))^2 f(x)dx\\&=E(X^2)-(E(X))^2 \end{aligned}\]

という関係があります。

平均\(\mu\)、標準偏差\(\sigma\)の正規分布Normal(μ,σ)について、その確率密度関数は

\[f(x) = \frac{1}{\sqrt{2\pi \sigma ^2} } \exp(-\frac{(x-\mu)^2}{2 \sigma^2})\]

です。この時点では、\(\mu ,\sigma^2\)は単なるパラメータ（実数）ですが、それが実際に平均と分散に一致することを証明しましょう。

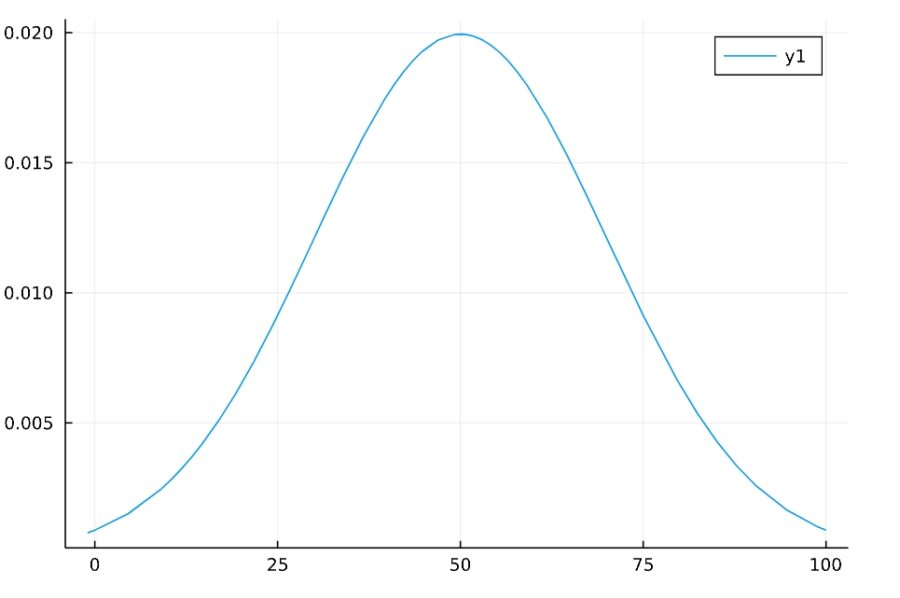
まずは特殊なケースとして、平均0で分散1のとき、標準正規分布Normal(0,1)を考えます。その分布に従う確率変数を\(Z\)、確率密度関数を

\[g(z) = \frac{1}{\sqrt{2\pi } } \exp(-\frac{z^2}{2 })\]

としましょう。

平均を計算すると、微積分学の基本定理から

\[\begin{aligned} E(Z) &= \int_{-\infty}^\infty s \frac{1}{\sqrt{2\pi } } \exp(-\frac{s^2}{2 })ds \\ &=[ -\frac{1}{\sqrt{2\pi }} \exp(-\frac{s^2}{2 })]_{-\infty}^\infty \\ &=0-0\\&=0 \end{aligned}\]

です。

また、\(Z^2\)の期待値は、部分積分によって計算できます。

\[\begin{aligned} &\frac{d}{ds}(- \frac{1}{\sqrt{2\pi } } \exp(-\frac{s^2}{2 }) )\\ &= s\frac{1}{\sqrt{2\pi } } \exp(-\frac{s^2}{2 })\end{aligned}\]

に気をつけて、

\[\begin{aligned} E(Z^2) &= \int_{-\infty}^\infty s (s \frac{1}{\sqrt{2\pi } } \exp(-\frac{s^2}{2 }))ds \\&= [-s \frac{1}{\sqrt{2\pi } } \exp(-\frac{s^2}{2 })]_{-\infty}^\infty \\ &+ \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi } } \exp(-\frac{s^2}{2 } )ds \\&=0+1 \\&=1\end{aligned}\]

です。前半の項が消えるのは、指数関数の減衰の強さによるものです。後半の積分が1となるのは、全体における積分（確率の合計）が1となるように確率密度関数を選んでいるからです。詳しくは、ガウス積分

\[\int_{-\infty}^\infty e^{-ax^2}dx = \sqrt{\frac{\pi}{a}}\]

において、\(a=\frac{1}{2}\)としたケースに対応しています。そこで\(\sqrt{2\pi}\)が出てくるので、係数がキャンセルするわけです。

参考：極座標変換による重積分の計算ガウス積分を例に

したがって、分散は

\[\begin{aligned} V(Z)&= E(Z^2)-(E(Z))^2 \\&=1-0 \\&=1 \end{aligned}\]

と求められました。

一般に、確率変数を平行移動したり定数倍すると、平均と分散は次のようになります。

\[E(cX+a) =cE(X)+a\]

\[V(cX+a)= c^2 V(X) \]

平均は定数倍され、平行移動によってそのまま移動します。分散は定数の2乗倍され、平行移動によっては変わりません。

正規分布に従う確率変数\(X\)と、標準正規分布に従う確率変数\(Z\)の間には、\(X =\sigma Z +\mu\)という関係があります（\(Z = \frac{X-\mu}{\sigma}\)）。したがって、