連続確率変数の平均（期待値）、分散の求め方：一様分布を例に

どうも、木村（@kimu3_slime）です。

今回は、連続確率変数の平均、分散の求め方を、一様分布を例に紹介します。

前提知識：連続確率分布とは：一様分布、正規分布を例に

連続確率変数の平均、分散の定義
一様分布の平均、分散の求め方
こちらもおすすめ

連続確率変数の平均、分散の定義

離散確率変数\(X\)の平均、分散は

\[E(X):= \sum_{k} x_k f(x_k)\]

\[V(X):= \sum_{k} (x_k-E(X))^2 f(x_k)\]

と定義されるのでした。

連続確率変数\(X\)についても、同様に定義できます。\(f\)をその確率密度関数としましょう。

\(X\)の平均（mean）、または期待値（expected value）は

\[E(X):= \int_{-\infty}^\infty x f(x)dx\]

です。分散（variance）は

\[V(X):= \int_{-\infty}^\infty (x-E(X))^2 f(x)dx\]

です。離散的な和\(\sum\)が連続的な和\(\int\)（積分）に対応しています。

分散の正の平方根\(\sqrt{V(X)}\)は標準偏差（standard deviation）と呼ばれます。

分散は、期待値を用いて次のように表すことができます。これは離散確率変数のケースと同様の議論です。

\[V(X)= E(X^2) – (E(X))^2\]

分散の定義式と、和の線形性から

\[\begin{aligned} V(X) &=\int_{-\infty}^\infty (x^2 -2xE(X)+(E(X))^2) f(x)dx\\&= \int_{-\infty}^\infty x ^2 f(x) dx -2E(X) \int_{-\infty}^\infty xf(x)dx \\&+(E(X))^2 \int_{-\infty}^\infty f(x)dx \\ &=E(X^2)-2(E(X))^2+(E(X))^2 \\ &= E(X^2) – (E(X))^2 \end{aligned}\]

となるためです。確率の合計が1であること\(\int_{-\infty}^\infty f(x)dx=1\)に注意しましょう。

ここで用いた、確率変数\(X^2\)の期待値の式\(E(X^2) =\int_{-\infty}^\infty x^2 f(x)dx \)は、それが定義です。一般に、連続関数\(g\)を合成した確率変数\(g(X)\)の期待値（expectation）は、

\[g(X):= \int_{-\infty}^\infty g(x)f(x)dx\]

と定義されます。この用語を使って分散の定義を表せば、

\[V(X) = E((X – E(X))^2)\]

です。

一様分布の平均、分散の求め方

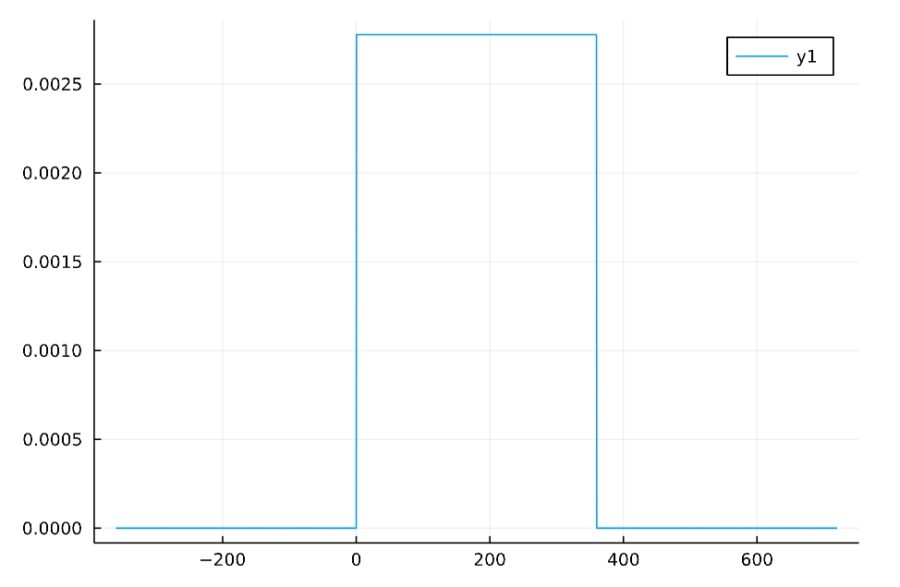
\(a\)以上\(b\)以下の連続一様分布Uniform(a,b)について、その確率密度関数は

\[f(x)= \begin{cases}\frac{1}{b-a} & (a \leq x \leq b )\\0 & (それ以外)\end{cases}\]

です。平均値と分散を求めてみましょう。

平均値は

\[\begin{aligned} E(X) &=\int_{a}^b x \frac{1}{b-a}dx \\&= \frac{1}{b-a}[\frac{1}{2}x^2]_a^b\\ &= \frac{1}{2}\frac{b^2-a^2}{b-a} \\ &= \frac{1}{2}(a+b) \end{aligned}\]

です。区間のちょうど真ん中に平均値があります。

分散を求めるために、\(X^2\)の期待値を計算しましょう。

\[\begin{aligned} E(X^2)&= \int_{a}^b x^2 \frac{1}{b-a}dx \\ &= \frac{1}{b-a}[\frac{1}{3}x^3]_a ^b \\ &= \frac{1}{3}\frac{b^3-a^3}{b-a} \\ &= \frac{1}{3}(b^2+ab+a^2)\end{aligned} \]

となります。したがって、分散は

\[\begin{aligned} V(X) &=E(X^2)-(E(X))^2\\&= \frac{1}{3}(b^2+ab+a^2) – \frac{1}{4}(a^2+2ab+b^2)\\ &= \frac{1}{12}(b^2-2ab+a^2)\\ &= \frac{1}{12}(b-a)^2\end{aligned}\]

と求められました。区間の幅\(b-a\)が長くなるほど、分散も大きくなります。

例えば\(a=0,b=360\)のときは、平均値\(180\)、分散は\(10800\)、標準偏差は約\(104\)です。

以上、連続確率変数の平均、分散の求め方を、一様分布を例に紹介してきました。

離散一様分布と比べると、結果は似ていますが、積分によって計算が楽になっているのが感じられますね。

木村すらいむ（@kimu3_slime）でした。ではでは。