離散確率変数の平均（期待値）、分散の求め方：一様分布を例に

どうも、木村（@kimu3_slime）です。

今回は、離散確率変数の平均、分散の求め方を、一様分布を例に紹介します。

前提知識：離散確率分布とは：一様分布、ベルヌーイ分布、二項分布、ポアソン分布を例に

離散確率変数の平均、分散の定義
一様分布の平均、分散の求め方
こちらもおすすめ

離散確率変数の平均、分散の定義

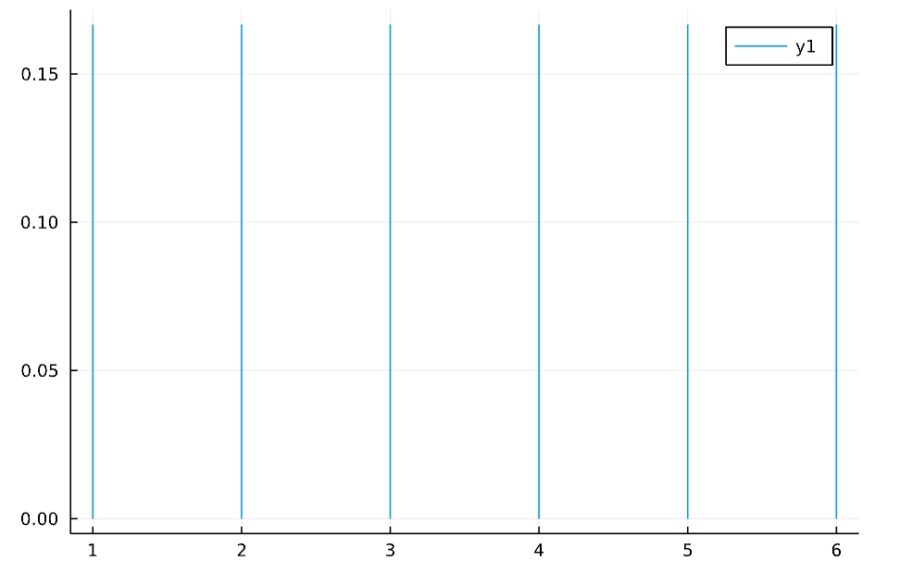
公平なサイコロを1回振るときに得られる値の平均値（期待値）は、「取りうる値×その確率」を足し合わせたものです。

\[1\times \frac{1}{6}+2\times \frac{1}{6}+\cdots+6 \times \frac{1}{6} \\= \frac{7}{2}=3.5\]

この考え方を一般化しましょう。確率分布\(P\)に従う離散確率変数を\(X\)、確率質量関数を\(f(x):=P(X=x)\)とします。確率変数が取りうる値を\(x_k\)とするとき、その確率は\(f(x_k)\)です。

したがって、確率変数の平均値（mean）、または期待値（expected value）は

\[E(X):= \sum_{k} x_k f(x_k)\]

と定義されます。和\(\sum_{k}\)は、確率変数の値が取りうる範囲全体に渡るものです。\(\mu = E(X)\)と書くことも。高校数学の記法では、確率質量関数の値を\(p_k =f(x_k)\)と表して、\(E= \sum_{k} x_k p_k\)と書きますが、同じことです。

データ（サンプル）の平均値と同じ文字の用語で考え方も似ていますが、別の概念であることに注意しましょう。確率変数の平均値は、理論的な＝確率的な平均値です。同じ分布に従うたくさんのデータを取ると、データの平均値は確率変数の期待値に近づいていきます（大数の法則）。

確率変数がどれだけ平均から離れた値を取りうるかを示す値、分散（variance）は

\[V(X):= \sum_{k} (x_k-E(X))^2 f(x_k)\]

と定義されます。\(\sigma ^2 = V(X)\)と書くこともあり、その正の平方根\(\sigma=\sqrt{V(X)}\)が標準偏差です。

サイコロを1回振るときに得られる値を\(X\)とすると、それは一様分布に従うので、\(f(k) = \frac{1}{6}\)です。分散を計算してみると、対称性から

\[\begin{aligned} V(X) &=\sum_{k=1}^6 (k-\frac{7}{2})^2 \cdot \frac{1}{6} \\ &= 2\sum_{k=1}^3 (k-\frac{7}{2})^2 \cdot \frac{1}{6} \\ &= \frac{\frac{25}{4}+\frac{9}{4}+\frac{1}{4}}{3} \\&= \frac{35}{12}\end{aligned}\]

となりました。およそ3ですね。

一般に分散は、期待値を用いて次のように表すことができます。

\[V(X)= E(X^2) – (E(X))^2\]

これは分散の定義式と、和の線形性から

\[\begin{aligned} V(X) &= \sum_{k} (x_k^2 -2x_kE(X)+(E(X))^2) f(x_k)\\&= \sum_{k}x_k ^2 f(x_k) -2E(X) \sum_{k}x_kf(x_k) \\&+(E(X))^2 \sum_{k}f(x_k)\\ &=E(X^2)-2(E(X))^2+(E(X))^2 \\ &= E(X^2) – (E(X))^2 \end{aligned}\]

となるためです。確率の合計が1であること\(\sum_{k}f(x_k)=1\)に注意しましょう。

これは便利な計算式で、連続確率変数についても同様の計算が可能です。

ここで用いた、確率変数\(X^2\)の期待値の式\(E(X^2) =\sum_{k}x_k ^2 f(x_k) \)は、それが定義です。一般に、連続関数\(g\)を合成した確率変数\(g(X)\)の期待値（expectation）は、

\[g(X):= \sum_{k} g(x_k)f(x_k)\]

と定義されます。この用語を使って分散の定義を表せば、

\[V(X) = E((X – E(X))^2)\]

です。

一様分布の平均、分散の求め方

\(a\)以上\(b\)以下の離散一様分布DiscreteUniform(a,b)について、その確率質量関数は

\[f(x) = \frac{1}{b-a+1}\]

です。平均値と分散を求めてみましょう。

平均値は

\[\begin{aligned} E(X) &=\sum_{k=a}^b k \frac{1}{b-a+1}\\&= \frac{1}{2}(b-a+1)(a+b)\frac{1}{b-a+1} \\ &= \frac{1}{2}(a+b) \end{aligned}\]

です。ここで、等差数列の和の公式\(S_n= \frac{1}{2}\times項数\times(初項+末項)\)を利用しました。

区間のちょうど真ん中に平均値があります。

分散を求めるにあたり、\(n=b-a+1\)と置きましょう。

数列の和の公式\(\sum_{k=1}^n k^2 = \frac{1}{6}n(n+1)(2n+1)\)、\(\sum_{k=1}^n k = \frac{1}{2}n(n+1)\)、\(\sum_{k=1}^n 1 = n\)より、

\[\begin{aligned} E(X^2)&=\sum_{k=a}^b k^2 \frac{1}{n} \\&= \frac{1}{n}\sum_{k=0}^{n-1} (k+a)^2 \\&= \frac{1}{n}\sum_{k=0}^{n-1}(k^2+2ak +a^2)\\ &= \frac{1}{n}(\frac{1}{6}(n-1)n(2n-1) \\ & +2a \frac{1}{2}(n-1)n+na^2)\\ &= \frac{1}{6}(n-1)(2n-1)+a(n-1) +a^2\end{aligned} \]

となるので、分散は

\[\begin{aligned} V(X) &=E(X^2)-(E(X))^2\\&=\frac{1}{6}(n-1)(2n-1)+a(n-1) +a^2 \\ &-(a+ \frac{n-1}{2})^2 \\ &= \frac{1}{6}(n-1)(2n-1)- \frac{1}{4}(n-1)^2\\ &=\frac{1}{12}(n-1)(2(2n-1)-3(n-1))\\ &= \frac{1}{12}(n+1)(n-1) \\&= \frac{1}{12}(n^2-1)\end{aligned}\]

と求められました。区間の幅\(n\)が長くなるほど、分散も大きくなります。

分散は2乗して計算しているので\(n^2\)が出てきますが、標準偏差を取ればおよそ区間の長さ\(n\)に比例した値が取り出せますね。\(\sqrt{\frac{n^2-1}{12}}=O(n)\quad(n\to \infty)\)です（オーダー記法）。

以上、離散確率変数の平均、分散の求め方を、一様分布を例に紹介してきました。

一般的な形を計算しようとすると少し難しいので、まずはサイコロやコイン投げのように具体的なケースから計算してみると良いでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。