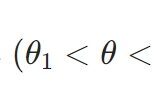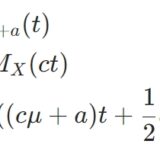モーメント生成関数とは：正規分布の平均と分散を例に

どうも、木村（@kimu3_slime）です。

今回は、モーメント生成関数とは何か、正規分布の平均と分散を例に紹介します。

モーメント生成関数とは
正規分布のモーメント生成関数
こちらもおすすめ

モーメント生成関数とは

\(X\)を離散または連続確率変数とします。\(X\)のモーメント生成関数（m.g.f.; moment generating function）とは、\(t \in \mathbb{R}\)として

\[M_{X}(t):= E(e^{tX})\]

と定義される関数です。積率母関数とも。

\(E\)は期待値です。\(f\)を\(X\)の確率（質量・密度）関数として、離散型ならば

\[E(e^{tX}) =\sum_{k=1}^\infty e^{tx_k} f(x_k) \]

連続型ならば

\[E(e^{tX}) = \int_{-\infty}^\infty e^{tx}f(x)dx \]

となります。

モーメント生成関数は、文字通りモーメントを生み出す関数です。

\(e^{tx}= \sum_{\ell=0}^\infty \frac{1}{\ell !}(tx)^\ell\)とテイラー展開しましょう。すると、

\[\begin{aligned} E(e^{tX}) &=\sum_{k=1}^\infty (\sum_{\ell=0}^\infty \frac{1}{\ell !}(tx)^\ell) f(x_k) \\ &=\sum_{\ell =0}^\infty \sum_{k=1}^\infty\frac{1}{\ell !}(tx)^\ell f(x_k) \\&= \sum_{\ell=0}^\infty \frac{t^\ell}{\ell !}E(X^\ell)\end{aligned}\]

となります。一般に、絶対収束する二重和は順序交換可能です。連続なケースでも、同様の議論ができます。ここでは、モーメント生成関数は存在し（級数や積分が収束する）、微分可能であると仮定しています。

得られた級数を\(t\)について項別微分をすると、

\[\frac{d}{dt}M_X (t) = \sum_{\ell=1}^\infty \frac{t^{\ell -1}}{(\ell -1)!}E(X^\ell)\]

\[\frac{d^n}{dt^n}M_X (t) = \sum_{\ell=n}^\infty \frac{t^{\ell -n}}{(\ell -n)!}E(X^\ell)\]

となるので、\(t=0\)のときを考えれば

\[M_X(0)= E(X^0)=1\]

\[\frac{d}{dt} M_X(0)= E(X)\]

\[\frac{d^n}{dt^n} M_X(0)= E(X^n)\]

が得られます。\(E(X^n)\)は、原点を中心とする\(n\)次のモーメントと呼ばれるものです。

モーメント母関数が求められれば、平均や分散などモーメントによって計算できる量が求められます。

また、モーメント母関数の一意性（もし2つのモーメント母関数が一致するなら、それらの確率変数の累積分布関数も一致する）という性質が知られています。

これを使って、確率変数を変換したときに平均や分散がどう変換されるかが決定できることがあります。

正規分布のモーメント生成関数

正規分布\(\mathrm{Normal}(\mu, \sigma^2)\)のモーメント生成関数は

\[M_X(t) = \exp(\mu t +\frac{1}{2} \sigma ^2 t^2)\]

となります。\(\exp\)は指数関数です。これを確かめてみましょう。

正規分布の確率密度関数は\(f(x)= \frac{1}{\sqrt{2\pi \sigma^2}}\exp( -\frac{(x-\mu)^2}{2\sigma^2})\)でした。指数部分を正規分布の形になるように平方完成すると、

\[\begin{aligned} E(e^{tX}) &= \frac{1}{\sqrt{2\pi \sigma^2}} \int_{-\infty}^\infty \exp(tx – \frac{(x-\mu)^2}{2\sigma^2})dx\\&= \frac{1}{\sqrt{2\pi \sigma^2}} \int_{-\infty}^\infty \exp(- \frac{(x-(\mu+\sigma^2 t))^2}{2\sigma^2}) \\&\quad \exp(\mu t +\frac{1}{2}\sigma ^2 t^2)dx\end{aligned}\]

となります。ここで

\[ \frac{1}{\sqrt{2\pi \sigma^2}} \int_{-\infty}^\infty \exp(- \frac{(x-(\mu+\sigma^2 t))^2}{2\sigma^2})dx =1\]

です、これは平均\(\mu+\sigma^2 t\)、分散\(\sigma^2\)の正規分布の確率密度関数の全区間における積分なので、合計は1となります。よって、

\[\begin{aligned} E(e^{tX}) &=\exp(\mu t +\frac{1}{2}\sigma ^2 t^2)\end{aligned}\]

となることがわかりました。

これを使って、正規分布の平均と分散を求めてみましょう。モーメント生成関数の微分は、

\[\frac{d}{dt}M_{X}(t)=(\mu +\sigma^2 t)\exp(\mu t +\frac{1}{2}\sigma ^2 t^2)\]

\[\begin{aligned} \frac{d^2}{dt^2}M_{X}(t)&=\sigma^2 \exp(\mu t +\frac{1}{2}\sigma ^2 t^2) \\&\quad+(\mu +\sigma^2 t)^2 \exp(\mu t +\frac{1}{2}\sigma ^2 t^2) \end{aligned}\]

となるので、1次（平均）、2次のモーメントは

\[E(X) = \frac{d}{dt}M_{X}(0) =\mu\]

\[E(X^2) = \mu^2+\sigma^2\]

です。よって、分散の性質から

\[\begin{aligned} V(X)&=E(X^2)-(E(X))^2 \\&=\mu^2+\sigma^2-\mu^2 \\&=\sigma^2 \end{aligned}\]

と求めることができました。

以上、モーメント生成関数とは何か、正規分布の平均と分散を例に紹介してきました。

モーメント生成関数は、確率変数を変数変換したときモーメントがどう変わるかを計算するのにも役立ちます。これについては別記事で紹介予定です。

木村すらいむ（@kimu3_slime）でした。ではでは。