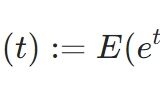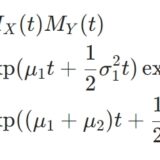どうも、木村(@kimu3_slime)です。
今回は、正規分布の線形変換が正規分布であることの、モーメント生成関数による証明を紹介します。
モーメント生成関数の性質
\(X\)を確率変数、定数\(a,c\)を使った線形変換された確率変数\(X+a\)と\(cX\)について考えましょう。そのモーメント生成関数はどうなるでしょうか。
期待値の平行移動、定数倍の性質を用いると、
\[\begin{aligned} M_{X+a}(t) &= E(e^{t (X+a)}) \\&= E(e^{t X}e^{ta})\\&= e^{at}E(e^{tX}) \\&=e^{at}M_{X}(t) \end{aligned}\]
\[\begin{aligned} M_{cX}(t) &= E(e^{ct X}) \\&= M_{X}(ct) \end{aligned}\]
となります。
正規分布の線形変換が正規分布であること
\(X\)を平均\(\mu \)、分散\(\sigma^2\)の正規分布に従う確率変数としましょう。このとき、その線形変換\(Y = cX+a\)はまた正規分布になります。
正規分布のモーメント生成関数は、\(M_{X}(t)=\exp(\mu t +\frac{1}{2}\sigma^2 t^2)\)でした。
モーメント母関数の性質を用いれば、
\[\begin{aligned} &\quad M_{cX+a}(t) \\&= e^{at} M_{X}(ct) \\&= \exp((c\mu +a) t+ \frac{1}{2}c^2 \sigma^2 t^2) \end{aligned}\]
となります。これは平均\(c\mu +a\)、分散\(c^2 \sigma^2\)の正規分布のモーメント生成関数です。
モーメント生成関数は分布を一意に定めるので、\(Y=cX+a\)は平均\(c\mu +a\)、分散\(c^2 \sigma^2\)の正規分布に従うことが示せました。
以上、正規分布の線形変換が正規分布であることの、モーメント生成関数による証明を紹介してきました。
期待値や分散を求められるだけでなく、分布を決定できるのがモーメント生成関数の強みですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Probability and Statistics: Pearson New International Edition
Pearson Education Limited (2013-07-30T00:00:01Z)
¥10,792 (中古品)
培風館 (1978-01-01T00:00:01Z)
¥5,280
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)