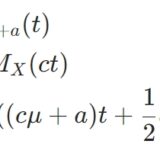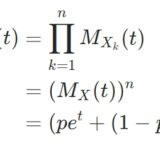独立な正規分布の和、平均が正規分布に従うこと（再生性）の証明

どうも、木村（@kimu3_slime）です。

今回は、独立な正規分布の和、平均が正規分布に従うことの証明を紹介します。

和のモーメント生成関数
独立な正規分布の和、平均が正規分布に従うこと
こちらもおすすめ

和のモーメント生成関数

一般論として、2つの独立な確率変数\(X,Y\)の和\(X+Y\)のモーメント生成関数を求めてみましょう。

\(X,Y\)が独立であるとき、それに同じ（可測）関数を合成した確率変数\(g(X),g(Y)\)も独立となります。したがって、\(e^{tX},e^{tY}\)は独立です。

\[\begin{aligned} M_{(X+Y)}(t) &=E(e^{t(X+Y)})\\&=E(e^{tX}e^{tY})\\&=E(e^{tX})E(e^{tY})\\&= M_{X}(t) M_{Y}(t) \end{aligned}\]

と積の形になります。

独立な正規分布の和、平均が正規分布に従うこと

確率変数\(X , Y\)は独立で、\(X\)は平均\(\mu_1\)・分散\(\sigma_1 ^2\)の正規分布、\(Y\)は平均\(\mu_2\)・分散\(\sigma_2 ^2\)の正規分布に従うとしましょう。

このとき、その和\(X+Y\)も正規分布となります。

平均\(\mu\)・分散\(\sigma^2\)のモーメント生成関数は\(\exp(\mu t +\frac{1}{2} \sigma ^2 t)\)であることに注意して、和のモーメント生成関数を計算しましょう。独立性から積によって計算でき、

\[\begin{aligned} M_{X+Y}(t) &= M_{X}(t)M_{Y}(t) \\&= \exp(\mu_1 t +\frac{1}{2} \sigma_1 ^2 t) \exp(\mu_1 t +\frac{1}{2} \sigma_2 ^2 t)\\ &=\exp((\mu_1 +\mu_2) t +\frac{1}{2}(\sigma_1^2 +\sigma_2^2 ) t^2)\end{aligned}\]

となります。モーメント生成関数は分布を一意に決定するので、\(X+Y\)は平均\(\mu_1 +\mu_2\)、分散\(\sigma_1 ^2 +\sigma_2 ^2\)の正規分布に従うことがわかりました。

独立な正規分布の和がまた正規分布となることは、正規分布の再生性（reproductive property）と呼ばれています。

\(X\)を平均\(\mu\)・分散\(\sigma ^2\)の正規分布に従う確率変数、\(X_1,\dots, X_n\)をその分布に従う独立な確率変数族とします。

このとき、標本平均\(M_n = \frac{1}{n}\sum_{k=1}^n X_k\)は正規分布に従います。

定数倍のモーメント生成関数の性質に注意して、

\[\begin{aligned} M_{M_n} (t) &= \prod_{k=1}^n M_{X_k} (\frac{t}{n})\\ &= (M_{X} (\frac{t}{n}))^n \\ &= \exp(n (\mu \frac{t}{n} +\frac{1}{2}\sigma^2 \frac{t^2}{n^2})) \\ &= \exp(\mu t +\frac{1}{2} \frac{\sigma^2}{n}t^2)\end{aligned}\]

となります。モーメント生成関数が分布を一意に決めることから、\(M_n\)は平均\(\mu\)・分散\(\frac{\sigma^2}{n}\)の正規分布に従います。

\(Z_ n := \frac{M_n – \mu}{\frac{\sigma}{\sqrt{n}}}\)を標準誤差と呼びます。

\(Z_n\)が、平均0・分散1の正規分布（標準正規分布）に従うことを確かめてみましょう。

定数和と定数倍のモーメント生成関数の性質から、

\[\begin{aligned} M_{Z_n}(t)&= M_{M_n-\mu} (\frac{1}{\frac{\sigma}{\sqrt{n}}} t) \\&= e^{-\mu \frac{1}{\frac{\sigma}{\sqrt{n}}} t} M_{M_n}(\frac{1}{\frac{\sigma}{\sqrt{n}}} t) \\&= e^{-\mu \frac{1}{\frac{\sigma}{\sqrt{n}}} t}\exp(\mu \frac{1}{\frac{\sigma}{\sqrt{n}}} t +\frac{1}{2} \frac{\sigma^2}{n} \frac{1}{\frac{\sigma^2}{n}} t^2)\\ &=\exp(0t +\frac{1}{2} 1 t^2)\end{aligned}\]

となります。モーメント生成関数が分布を一意に定めることから、標準誤差\(Z_n\)は標準正規分布に従うことが示せました。

以上、正規分布の和、平均が正規分布に従うことの証明を紹介してきました。

正規分布は、数学的な性質がよくて扱いやすいことがわかりますね。、この性質は正規分布の区間推定に応用されています。

木村すらいむ（@kimu3_slime）でした。ではでは。