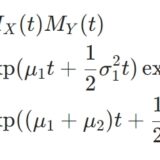どうも、木村(@kimu3_slime)です。
今回は、ベルヌーイ分布の和が二項分布である証明について、モーメント生成関数を使って紹介します。
ベルヌーイ分布のモーメント生成関数
結論を示すために、ベルヌーイ分布、二項分布のそれぞれのモーメント生成関数を調べましょう。
\(X\)を確率\(p\)のベルヌーイ分布に従う確率変数とするとき、その確率質量関数は
\[f_X(x)= \begin{cases}1-p & (k=0 )\\p & (k=1)\end{cases}\]
です。したがって、モーメント生成関数は
\[\begin{aligned} M_X(t) &= E(e^{tX}) \\&= e^{0t}f_X (0)+e^{1t}f_X(1)\\&= pe^t +(1-p)\end{aligned}\]
となります。
二項分布のモーメント生成関数
\(Y\)を試行回数\(n\)・確率\(p\)の二項分布に従う確率変数とするとき、その確率質量関数は
\[f_Y(x)= C(n,x) p^{x} (1-p)^{n-x}\]
\(x=0,1,2,\dots, n\)、\(C(n,x)\)は二項係数です。したがって二項定理より、モーメント生成関数は
\[\begin{aligned} M_Y(t) &= E(e^{tY}) \\&= \sum_{k=0}^n e^{tk}f_Y (k)\\&= \sum_{k=0}^n C(n,k) ( p e^{t})^k (1-p)^{n-k} \\&= (pe^t +(1-p))^n\end{aligned}\]
となります。
ベルヌーイ分布の和が二項分布である
\(X_1,\dots,X_n\)をベルヌーイ分布\(X\)に従う独立な確率変数族としましょう。
このとき、その和\(S_n =X_1+\cdots +X_n\)は試行回数\(n\)・確率\(p\)の二項分布に従うことを示しましょう。
独立な確率変数族の和のモーメント生成関数は、それぞれのモーメント生成関数の積となります。したがって、
\[\begin{aligned} M_{S_n}(t) &= \prod _{k=1}^n M_{X_k}(t) \\&= (M_{X}(t))^n \\&=(pe^t +(1-p))^n \end{aligned}\]
となります。これは二項分布のモーメント生成関数です。
一般にモーメント生成関数は分布を一意に決めるので、和\(S_n\)は試行回数\(n\)・確率\(p\)の二項分布に従うことが示せました。
以上、ベルヌーイ分布の和が二項分布である証明について、モーメント生成関数を使って紹介してきました。
二項分布はベルヌーイ試行の和であるというのは基本的な解釈ですが、それを数式の上でも確かめられると良いですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Probability and Statistics: Pearson New International Edition
Pearson Education Limited (2013-07-30T00:00:01Z)
¥10,792 (中古品)
培風館 (1978-01-01T00:00:01Z)
¥5,280
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)
こちらもおすすめ
離散確率分布とは:一様分布、ベルヌーイ分布、二項分布、ポアソン分布を例に
独立な正規分布の和、平均が正規分布に従うこと(再生性)の証明