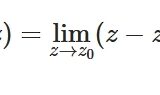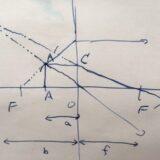
幾何学・相似の応用:レンズの公式の証明

微積分の応用:1次反応の半減期、放射性炭素年代測定法とは
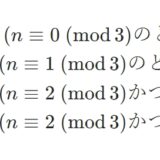
n^nを3で割ったあまりの規則性、証明
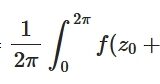
複素解析・調和関数に関する平均値の性質とは、例と証明
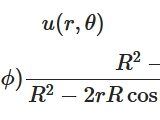
複素解析におけるポアソンの積分公式とは、ポアソン核との関連
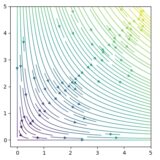
流体の複素ポテンシャル、速度ポテンシャル、流れ関数、流線とは
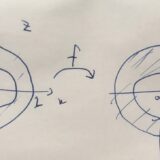
中心のずれた円環領域におけるポテンシャルの求め方:線形分数変換の応用

複素解析における最大値の原理とは:例、注意点
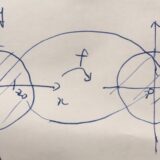
単位円盤を単位円盤に写す線形分数変換とは、例
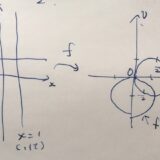
線形分数変換とは:反転1/zを例に
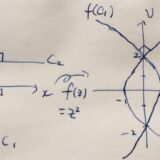
等角写像とは、性質:z^2を例に
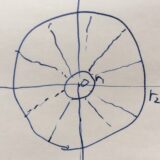
複素ポテンシャルとは:円環領域を例に
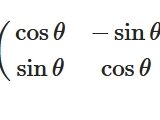
ラプラシアンが回転不変であること:2次元での証明
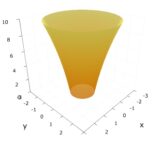
円環領域におけるポテンシャル:2次元ラプラス方程式の解き方
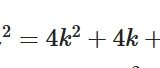
平方数と倍数:n^2がmの倍数ならばnはmの倍数であることの証明
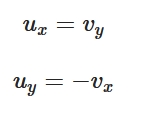
共役調和関数とは:定義と例
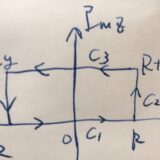
ガウス関数のフーリエ変換の計算法:コーシーの積分定理
三角関数の有理関数の積分:留数定理による計算