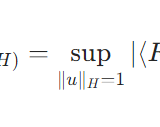どうも、木村(@kimu3_slime)です。
今回は、コンパクト対称作用素が作用素ノルムを固有値として持つことの証明を紹介します。
導入
\(H\)をヒルベルト空間(完備な内積空間)、\(F:H \to H\)をコンパクトで対称な線形作用素とします。
有限次元(線形代数)においては、対称行列は常に対角化可能という良い性質を持っていました。コンパクト対称作用素については、その一般化した結果としてヒルベルト・シュミットの定理が知られています。
- 固有値はすべて実数
- \(|\lambda _{n+1}| \leq |\lambda_n|\)と\(\lim_{n \to \infty}\lambda_n = 0\)を満たす可算無限個の固有値\((\lambda _n)\)が存在する。
- 固有関数系が像\(F(H)\)の完全正規直交系となるようにできる。
今回はその一部分の結果として、\(F\)の作用素ノルム\(\|F\|_{B(H,H)},-\|F\|_{B(H,H)}\)の少なくともひとつは、\(F\)の固有値であることを示しましょう。
作用素についても固有値、固有ベクトルの定義は行列と同じです。\(F(u)=\lambda u\)を満たす\(\lambda \in \mathbb{C}\)、\(u\in H, u \neq 0\)が存在するとき、\(\lambda \)を\(F\)の固有値(eigenvalue)、\(u\)を固有ベクトル(eigenvector)や固有関数(eigenfunction)と呼びます。
証明
\[\|F\|_{B(H,H)} = \sup_{\|u\|_{H}=1} |\langle F(u),u\rangle|\]
から出発しましょう。\(F\)はコンパクト、したがって有界なので、このノルムは有限値です。
\(F=O\)(ゼロ作用素)のときは、作用素ノルムの正定値性から\(\|F\|_{B(H,H)}=0\)です。(\(H=\{0\}\)でなければ、)\(u \in H\)で\(\|u\|_H =1\)を満たすものを選べば、\(Ou = 0 u = 0\)が成り立つので、\(0\)が固有値、\( u \neq 0\)がその固有ベクトルです。以降では、\(F \neq O\)のケースを扱いましょう。
上限の点列による特徴づけから、\(\lim_{n\to \infty} |\langle F(u_n),u_n\rangle|=\|F\|_{B(H,H)} \)、\(\|u_n\|_H=1\)を満たす\(H\)の点列\((u_n)\)が存在します。\(\|F\|_{B(H,H)} > 0\)なので、十分先の項では\(\langle F(u_n),u_n\rangle\)は定符号で、\(\lim_{n\to \infty} \langle F(u_n),u_n\rangle=\|F\|_{B(H,H)} \)または\(\lim_{n\to \infty} \langle F(u_n),u_n\rangle=-\|F\|_{B(H,H)} \)です。いずれのケースでも、これを\(\alpha : = \pm\|F\|_{B(H,H)} \)と置きましょう。
\((u_n)\)は有界で、\(F\)はコンパクト作用素なので、\((F(u_n))\)は収束する部分列を持ちます。それを\(F(u_{n{_k}}) \to v\quad (k \to \infty)\)としましょう。
\(F(u)= \alpha u\)の形を作るために、それを近似するノルムを評価します。すると、内積とノルムの関係、内積の線形性、\(F\)の対称性、作用素ノルムの定義から、
\[\begin{aligned} &\|F(u_{n{_k}}) -\alpha u_{n{_k}}\|_H^2 \\ &= \langle F(u_{n{_k}}) -\alpha u_{n{_k}},F(u_{n{_k}}) -\alpha u_{n{_k}}\rangle_H \\&= \langle F(u_{n{_k}}),F(u_{n{_k}}) \rangle_H +\langle F(u_{n{_k}}),-\alpha u_{n{_k}}\rangle_H \\&\quad +\langle -\alpha u_{n{_k}}, F(u_{n{_k}})\rangle_H +\alpha ^2\langle u_{n{_k}}, u_{n{_k}}\rangle_H \\&= \|F(u_{n{_k}})\|_H^2 -2\alpha\langle F(u_{n{_k}}),u_{n{_k}}\rangle_H +\alpha^2 \|u_{n_k}\|_H^2 \\& \leq 2\alpha ^2 \|u_{n_k}\|_H^2-2\alpha\langle F(u_{n{_k}}),u_{n{_k}}\rangle_H\\&= 2\alpha ^2 -2\alpha\langle F(u_{n{_k}}),u_{n{_k}}\rangle_H \\& \to 2\alpha ^2 -2\alpha ^2 \quad(k \to \infty) \\&=0\end{aligned}\]
です。したがって、三角不等式から
\[\begin{aligned} &\|\alpha u_{n{_k}} -v\|_H \\ &\leq \|\alpha u_{n{_k}}- F(u_{n{_k}})\|_H +\|F(u_{n{_k}})- v\| \\& \to 0 \quad(k \to \infty)\end{aligned}\]
です。\(\alpha \neq 0\)は番号によらない定数なので、収束する数列の定数倍は収束し、\(u_{n{_k}} \to \frac{1}{\alpha}v\quad(k \to \infty)\)です。これを\(u:= \frac{1}{\alpha}v\)と置きましょう。
\(F\)は有界ゆえに連続なので、\(F(u_{n{_k}}) \to F(u) \)です。\(F(u_{n{_k}}) \to v\quad (k \to \infty)\)でもあったので、極限の一意性から\(F(u)=v\)です。よって、\(F\)の線形性より\(F(v)=\alpha v\)となります。
\(v=0\)と仮定すると、\(\|u_n\|_H=1\)から\(\|\alpha u_{n{_k}}\|_H = |\alpha|>0 \)で、\(\alpha u_{n{_k}} \to v\quad(k \to \infty)\)と収束することに矛盾します。したがって、\( v \neq 0\)です。
よって、\(\alpha = \pm\|F\|_{B(H,H)} \)(いずれか)、\( v \neq 0\)で、\(F(v)=\alpha v\)を満たすので、\(\alpha\)が固有値、\(v\)がその固有ベクトルとして存在することが示せました。
以上、コンパクト対称作用素が作用素ノルムを固有値として持つことの証明を紹介してきました。
コンパクト性から固有値の定義の近似式が作れて、対称性からノルムの二乗で展開される内積部分が処理できる、という流れでした。
この結果を発展させたヒルベルト・シュミットの定理については、別記事にて。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)