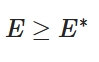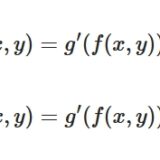どうも、木村(@kimu3_slime)です。
今回は、フーリエ係数の減衰について、リーマン・ルベーグの補題とは何か、その証明を紹介します。
フーリエ係数の減衰
フーリエ係数\(a_n,b_n\)は、\(n\to \infty\)としたときどうなるでしょうか。具体例を見てみましょう。
矩形波のフーリエ係数
\[ \begin{aligned}a_n =0\end{aligned} \]
\[ \begin{aligned} b_n &= \begin{cases}\frac{4}{n\pi}& (nは奇数 )\\0 & (nは偶数)\end{cases} \end{aligned} \]
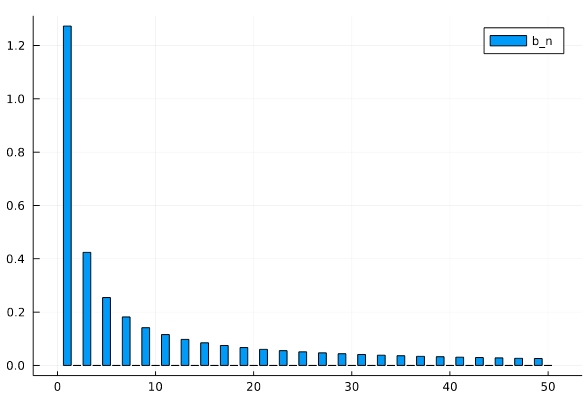
絶対サイン波のフーリエ係数
\[ \begin{aligned} a_n &= \begin{cases}-\frac{4}{ (n^2-1)\pi} & (nが偶数 )\\0 & (nが奇数)\end{cases}\end{aligned} \]
\[ \begin{aligned}b_n=0\end{aligned} \]
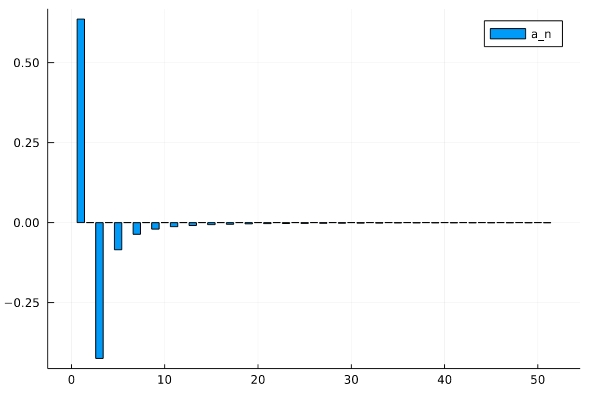
\[ \begin{aligned}\lim_{n\to \infty}a_n =0,\quad \lim_{n\to \infty}b_n =0\end{aligned} \]
と減衰しています。
リーマン・ルベーグの補題
この結果は偶然ではありません。関数\(f\)がフーリエ級数展開できるとき、例えば二乗可積分(\(f\in L^2\))のとき、必ず
\[ \begin{aligned}\lim_{n\to \infty}a_n =0,\quad \lim_{n\to \infty}b_n =0\end{aligned} \]
が成り立ちます。
フーリエ係数の定義に遡ると、それは
\[ \begin{aligned}\lim_{n\to \infty} \int_{-\pi}^\pi f(x) \cos nx dx =0\end{aligned} \]
\[ \begin{aligned}\lim_{n\to \infty} \int_{-\pi}^\pi f(x) \sin nx dx =0\end{aligned} \]
を意味します。これはリーマン・ルベーグの補題(Riemann–Lebesgue lemma)という名前で知られる主張です。
フーリエ級数の議論抜きにこの式だけパッとみると、自信を持って成り立つとはすぐには言いにくそうですね。
証明
では、リーマン・ルベーグの補題を証明しましょう。
今回は、それをベッセルの不等式
\[ \begin{aligned}2a_0^2 +\sum_{n=1}^\infty (a_n^2+b_n^2)\\ \leq \frac{1}{\pi}\int_{-\pi}^{\pi} (f(x))^2 dx\end{aligned} \]
から示します。\(f\)が2乗可積分なので、右辺は有限値で、したがって左辺も有限です。
さらに、
\[ \begin{aligned}\sum_{n=1}^\infty a_n^2 \\ < 2a_0^2 +\sum_{n=1}^\infty (a_n^2+b_n^2)\end{aligned} \]
\[ \begin{aligned}\sum_{n=1}^\infty b_n^2 \\ < 2a_0^2 +\sum_{n=1}^\infty (a_n^2+b_n^2)\end{aligned} \]
と比較することで、左辺の級数は収束します。
\[ \begin{aligned}\lim_{n\to \infty}a_n^2 =0\end{aligned} \]
\[ \begin{aligned}\lim_{n\to \infty}b_n^2 =0\end{aligned} \]
です。\(f(x)=\sqrt{x}\)の(点列)連続性から、
\[ \begin{aligned}\lim_{n\to \infty}a_n =0\end{aligned} \]
\[ \begin{aligned}\lim_{n\to \infty}b_n =0\end{aligned} \]
がわかりました。
今回は、\(f\)が2乗可積分という仮定で示しましたが、リーマン・ルベーグの補題は\(f\)が(絶対)可積分というより弱い仮定で成り立ちます。
その証明は吉田「ルベーグ積分入門」や黒田「関数解析」を参照してください。
以上、フーリエ係数の減衰について、リーマン・ルベーグの補題とは何か、その証明を紹介してきました。
ベッセルの不等式を使うと、係数からなる級数が有限値として収束することがわかり、そこから必然的に係数の減衰がわかります。
具体的にフーリエ係数を計算すると、その係数が減衰することは見て取れますが、その背後にこんな事実があると知ってもらえたら嬉しいです。
木村すらいむ(@kimu3_slime)でした。ではでは。
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
日本評論社 (2021-03-15T00:00:00.000Z)
¥3,960
共立出版 (1980-11-01T00:00:01Z)
¥5,390
東京大学出版会 (1989-12-01T00:00:01Z)
¥1,353 (中古品)
こちらもおすすめ
矩形波とは:フーリエ級数展開の求め方、ギブス現象、ライプニッツの級数
フーリエ級数の収束条件:L^2収束、一様収束、不連続点での値
フーリエ係数の最良性とは:証明、ベッセルの不等式、パーセバルの等式
関数の連続(極限)と数列連続(点列連続)の定義が同値であることの証明