線形写像、表現行列をなぜ学ぶか：同型写像の考え方

どうも、木村（@kimu3_slime）です。

線形代数の抽象論、特に線形写像や表現行列をなぜ学ぶのか。僕は初めて学ぶときはよくわかっていなかった気がします。

今回は、同型写像という考え方をはっきりと示すことで、線形代数の抽象的な理論が具体的なベクトル・行列の理論に落とせることを、具体例を通じて紹介します。

抽象的な対象を数ベクトル・行列に対応させる
こちらもおすすめ

抽象的な対象を数ベクトル・行列に対応させる

線形代数学の最初には、ユークリッド空間（数ベクトル空間）\(\mathbb{R}^N\)や行列\(A\)を扱うことが多いでしょう。その後、抽象的な線形空間\(V\)や線形写像\(f:V\to W\)を考えることがあります。

線形空間の定義や、線形写像の定義は、ユークリッド空間\(\mathbb{R}^N\)や行列\(A\)が持つ性質を取り出し、抽象化したものです。

このように抽象化して何が嬉しいかというと、ユークリッド空間や行列以外の数学的対象を、ユークリッド空間や行列の世界に落とし込むことができるのです。ベクトルや行列の理論が適用できる幅がすごく広がるんですね。

微分方程式と線形空間

そのことを、今回は微分方程式

\[ \begin{aligned}\frac{d^2f}{dx^2} (x) – f(x)=0\end{aligned} \]

を例に紹介します。

この方程式は線形方程式に分類され、解の集合\(V:=\{f \mid\frac{d^2f}{dx^2} (x) – f(x)=0 \}\)は線形空間となります。

\(V\)を解空間と言いますが、今回はその次元が2であると知られています。

詳しくは：線形微分方程式はなぜ指数関数e^{λt}と仮定して解いて良いか

特に、\(f_1(x)=\cos x\)、\(f_2 =\sin x\)と置くと、\(f_1,f_2\)は\(V\)の基底です。つまり、すべての解はコサインとサインの線形結合で表されます。

同型写像で対応させる

微分方程式には、線形写像が隠れています。それは微分作用素と呼ばれるものです。

\(D:V\to V\)を\(Df (x):=\frac{df}{dx}(x)\)と置くと、\(D\)は線形写像になります（微分の線形性）。

微分方程式とは、微分作用素という線形写像によって定まる部分空間\(V=\{f \mid (D^2 -I)f=0 \}\)とも言えるわけです。線形方程式を一般的に記述する手段として、線形写像というものが考えられます。

（今回は\(V\)の基底を知っているものとして議論し始めましたが、それらは\(D\)の固有ベクトルを求めることによって見つけられます。）

（今回は微分方程式が線形だったので解の集合は線形空間となりましたが、一般には線形空間とはならないことに注意しましょう。線形方程式に対してだけ線形代数の議論は使えます。）

さて、線形空間\(V\)や線形写像\(D\)はどんなものなのでしょうか？　それを解き明かすひとつの考え方が、同型写像です。

一般に、線形写像\(F: V \to W\)が全単射のとき、それを線形同型写像（linear isomorphism）と呼びます。

同型写像があると、2つの線形空間\(V,W\)の要素を一対一に対応させ、同一視することができます。特に、同型写像があるならば、\(\dim V = \dim W\)と次元が等しくなければなりません。

今回の具体例\(V=\{f \mid\frac{d^2f}{dx^2} (x) – f(x)=0 \}\)、\(f_1(x)=\cos x\)、\(f_2 =\sin x\)を、2次元のユークリッド空間\(\mathbb{R}^2\)へと対応させましょう。

\(F:\mathbb{R}^2 \to V\)を、\(F(x_1,x_2)=x_1 f_1+x_2f_2\)により定めましょう。\(f_1,f_2\)は線形独立なので、\(F\)は単射です。\(f_1,f_2\)の線形結合ですべての\(V\)の要素を表せるので、\(F\)は全射です。すなわち、\(F\)は全単射な線形写像、同型写像であるとわかりました。

特に、\(e_1 =(1,0),e_2=(0,1)\)という\(\mathbb{R}^2\)の標準基底を考えましょう。その同型写像による像は、\(F(e_1)=f_1\)、\(F(e_2)=f_2\)となっています。基底が基底に移り合っており、対応関係がありますね。

同型写像\(F\)は全単射なので、逆写像\(F^{-1}\)が存在します。それは\(F^{-1}(f_1)=e_1\)、\(F^{-1}(e_2)=e_2\)といったように、\(V\)のベクトルを\(\mathbb{R}^2\)のベクトルとして読み替えることもできるわけです。

線形写像を行列によって表現する

同型写像を使うと、線形写像\(D:V\to V\)を行列として表現することができるようになります。

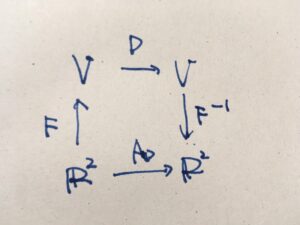
ひとまず、\(D\)に対応するような行列があるとして、それを\(A_D\)という記号で置きましょう。\(A_D\)は\(2\times2\)の正方行列で、\(A_D: \mathbb{R}^2 \to \mathbb{R}^2\)です。

上の図の対応関係を使って、\(A_D\)を求めてみましょう。\(A_D\)のインプットは\(\mathbb{R}^2\)で、アウトプットは\(\mathbb{R}^2\)です。インプット\(x\)を\(F\)で写すと\(F(x)\)、それを\(D\)で写すと\(D(F(x))\)、それを\(F^{-1}\)で戻すと\(F^{-1}(D(F(x)))\)となります。これを\(D\)により定まる対応関係と見るわけです。

\(F^{-1}(D(F(x)))\)を、\(V\)の基底、同型写像や\(D\)の定義を使って、具体的に計算してしましょう。コサインとサインなので、\(Df_1 =-f_2\)、\(Df_2 =f_1\)となることに注意。

\[ \begin{aligned} A_D x &=F^{-1}(D(F(x))) \\ &= F^{-1}(D(F(x))) \\ &= F^{-1}(D(x_1f_1+x_2f_2)) \\&=F^{-1}(-x_1f_2+x_2f_1)\\ &=x_2 e_1 -x_1 e_2\\ &= \begin{pmatrix} 0&1 \\-1&0 \end{pmatrix} \begin{pmatrix} x_1\\x_2 \end{pmatrix}\end{aligned} \]

よって

\[ \begin{aligned}A_D :=\begin{pmatrix} 0&1 \\-1&0 \end{pmatrix} \end{aligned} \]

と定めれば良いことがわかりました。これを線形写像\(D\)の表現行列（matrix representation）、行列による表現と言います。

未知の線形写像があったとしても、同型写像を使えば、数ベクトル空間の間の線形写像：行列として表すことができます。線型写像の定義は抽象的に見えますが、結局は行列と同じように扱えるので便利ですね。

例えば、線形写像のランク、固有値・固有ベクトル、対角化といった問題が、行列と同じようにして考えられるわけです。数ベクトル空間以外の線形空間や線形写像にも、線形代数の枠組みは使えます。

特に、今回の微分方程式の表現行列は、2階の微分方程式を連立線形常微分方程式を見ることに対応しています。

\(u_1(t) = f(t)\)、\(u_2 =\frac{df}{dt}(t)\)、\(u=(u_1,u_2)\)と置くと、もとの微分方程式\(\frac{d^2f}{dx^2} (x) – f(x)=0\)は

\[ \begin{aligned}\frac{du}{dt}(t) = A_D u\end{aligned} \]

という微分方程式と同値です。行列により表される連立微分方程式（線形微分方程式系）は、指数行列で\(u(t) = e^{tA} u_0\)と解けることが知られています。

実際、今回の例で指数行列を計算すると

\[ \begin{aligned}\exp (tA_D) =\begin{pmatrix} \cos t& \sin t \\-\sin t& \cos t \end{pmatrix} \end{aligned} \]

となります。初期条件を\(u_0 =(x_1,x_2)\)とすれば、\(u_1(t) = f(t) = x_1 \cos t +x_2 \sin t\)です。連立させていないときに得た解と一致していることがわかりますね。