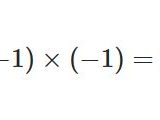論理学の入門ロードマップ：大学数学に必要な論理学とは

どうも、木村（@kimu3_slime）です。

大学数学を学ぶために必要な最小限の基礎的な能力は、論理学（と集合論）です。論理学は、大学数学だけでなく、中学校や高校の数学の議論全般の基礎になるもの。また、論理学自体は、科学や政治について論じるときなど、異なる背景を持った人々が、誤解なく伝わりやすい議論をするのに役立つ学問です。

にもかかわらず、論理学は、小中高大学で、それほどの重点を置かれて教えられていないと僕は思っています。そこで、当サイト『趣味の大学数学』では、特に数学に役立つ論理学の記事を増やし、論理学に入門しやすくしたいと思いました。

論理学入門ロードマップ

論理学入門ロードマップ

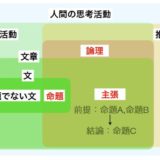
まず、「論理学」と呼ばれる分野には、何が含まれ、どのような順序で学んだ方が良いのか。それを僕なりにまとめたのが、次のロードマップです。

高校数学で学ぶ「集合と論理」では、命題を記号で表し、その間に成り立つ性質（否定、対偶、ド・モルガンの法則）を扱います。これは、記号論理学のうちの命題論理と呼ばれるものの入門です。

また、大学数学の教科書の最初の方で「集合と論理」が扱われることがありますが、これは命題論理に合わせ、述語論理が含まれることが多いです。

「論理学」という分野の分類を、おおざっぱに言えば

伝統的論理学：日常言語に適用できる論理。古典論理、アリストテレス的論理学とも。
記号論理学：形式言語に限定された論理。形式論理学とも。
数理論理学：数学、計算機科学の基礎としての論理。数学基礎論とも。

です。特に、伝統的論理学と記号論理学は、学問を志すあらゆる人が知っておきたいもので、それを教養論理学と呼ぶことにしました。数理論理学は、数学や計算機科学を専門とする人が学ぶと良いでしょう。

教養論理学を大学1年生で理解しておくと、数学や論理を駆使する学問を学びやすくなるほか、文章の読解、文章作成・論述や論述（technical writing）、ディベート、プレゼンテーションなど、あらゆるアウトプットの基礎を身につけられるでしょう。わかりやすい作文・プレゼン方法に関する本や、ビジネス書で言われる「ロジカル・シンキング」「クリティカル・シンキング」は、教養論理学にもとづいていると思われます。

大学数学の基礎としては、記号論理学を身に着けておきたいものです。しかし、大学の数学の講義・教科書では当たり前のものとされたり、部分的にしか触れられなかったりします。また、一般の解説書だと数学への応用が踏まえられていないし、あるいは専門書だと数理論理学に寄っていて初学者には難しすぎることがあります。学術の取得に役立つだけでなく、物の考え方と伝え方の基礎を与えてくれるのが論理学だと思っているので、大学一年生の教養として、記号論理学は必修にして良いレベルの価値があると僕は考えています。

当サイトの論理学の解説記事としては、次のものがあります。記事を増やし、教養論理学については完結した学びが得られるようなサイトにしていきたいと思います。