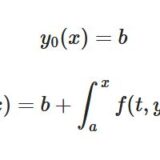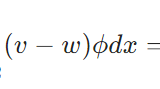
「関数解析」の記事一覧
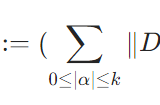
ソボレフ空間W^{k,p}・H^kが線形、ノルム、内積空間となることの証明
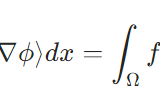
弱形式、弱解とは:ポアソン方程式を例に
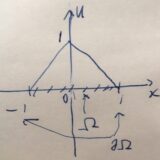
境界で0のソボレフ空間W_0^{k,p},H_0^kとは
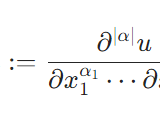
ソボレフ空間W^{k,p},H^kとは:多重指数、ノルム、内積
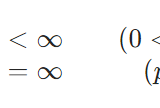
p乗可積分な関数とは:負のべき乗、L^1だがL^2でない例
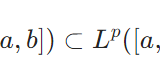
有界閉区間上の連続関数はp乗可積分であることの証明
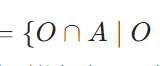
相対位相、部分集合における開集合・閉集合とは:ユークリッド空間の位相を例に
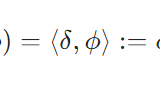
超関数、超関数微分とは:ディラックのデルタ関数を例に
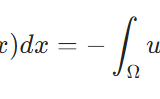
弱微分、ソボレフ空間W^{k,p},H^kとは:簡単な例
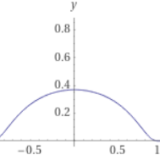
テスト関数C_c^∞、関数の台とは:簡単な例
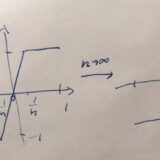
連続関数のなす空間がL^pノルムで完備でないことを示す例
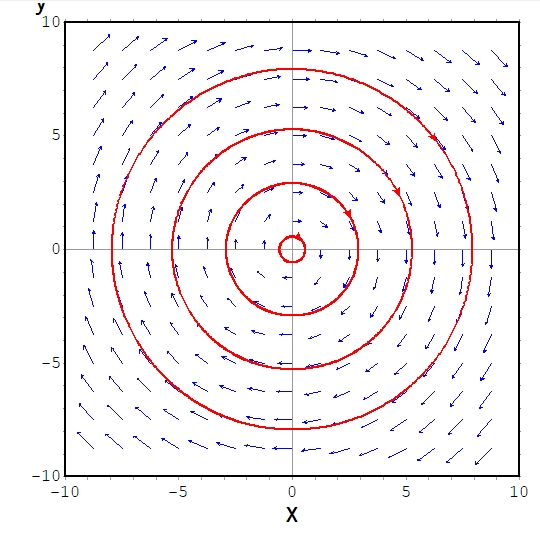
解作用素、抽象力学系とは:偏微分方程式の力学系入門
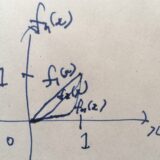
関数列の各点収束、一様収束とは、例と違い、求め方
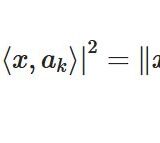
ベッセルの不等式・パーセバルの等式とは:有限のケースで証明
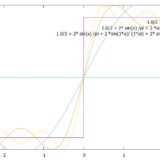
三角関数の直交性とは:フーリエ級数展開と関数空間の内積
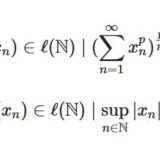
数列空間l^pとは、性質:ノルム、内積、無限次元
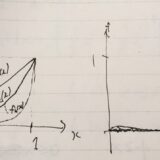
関数列の収束:各点収束、一様収束、L^p収束とは
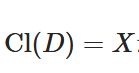
稠密性とは:有理数、ワイエルシュトラスの近似定理を例に