どうも、木村(@kimu3_slime)です。
今回は、グローバルアトラクターとは:散逸系における存在、例を紹介します。
定義
力学系におけるアトラクターとは、おおざっぱに言えば、周囲の状態をすべて引き寄せるような部分集合のことです。
\((H, (S(t)))\)を抽象力学系、\(A \subset H\)を空集合でないとしましょう。
\(A\)がグローバルアトラクター(global attractor)であるとは、
- コンパクトかつ正の不変集合であるような(集合の包含について)最大の部分集合であって、
- 有界な集合を誘引する「すべての有界な集合\(K \subset H\)について、\(\lim_{t \to \infty} d(S(t)K, A)=0\)」ような最小の空でない部分集合
です。ただし、\(d(\cdot ,\cdot)\)は集合間の距離を表します。
引き寄せる・誘引する(attract)という言葉が、アトラクターという用語の由来です。
引き寄せるような不変集合という点では、漸近安定な平衡解の一般化と言えるでしょう。
最も簡単な例として、\(\mathbb{R}\)における常微分方程式\(\frac{dx}{dt}=-x\)によって決まる力学系を考えましょう。
解は\(S(t)x_0 =x(t)= e^{-t}x_0\)です。
この系において、\(A=\{0\}\)はグローバルアトラクターです。やや細かいですが、条件をひとつずつ確認していきましょう。
まず、1点集合なので、有界な閉集合であり、したがってコンパクトです。また、すべての\(a \in A\)に対し、\(S(t)a =S(t)0 =0\)なので、正の不変集合です(\(x(t)=0\)は平衡解)。
\(A\)はコンパクトかつ正の不変集合のうち、最大のものです。仮に\(B \supsetneqq A\)で、コンパクトかつ正の不変集合であるものが存在したとしましょう。\(S(t)B = \{e^{-t}b \mid b \in B\}\)と時間経過で縮んでいくので、\(b \neq 0\)なる要素があるとき、例えば\(S(1)B \neq B\)です。これは\(B\)が不変集合であることに矛盾します。よって\(A\)の最大性が言えました。
\(K \subset \mathbb{R}\)を有界集合とすると、\(K\subset [-R,R]\)を満たす\(R>0\)が存在します。また、像の性質から\(S(t)K \subset S(t)[-R,R]\)です。上限はより広い範囲で考えた方が大きくなるので、\(d(S(t)K,A)= \sup_{b \in S(t)K}d(b,0) \leq \sup_{b \in S(t)[-R,R]}d(b,0)\)です。ここで、\(S(t)[-R,R]=[-e^{-t}R,e^{-t}R]\)なので、\(\sup_{b \in S(t)[-R,R]}d(b,0) =e^{-t}R\)となります。よって、\(0 \leq d(S(t)K,A) \leq e^{-t}R \to 0\,(t \to \infty)\)なので、はさみうちの原理から\(\lim_{t \to \infty} d(S(t)K, A)=0\)が示せました。
\(A=\{0\}\)なので、これ以上小さな空でない集合は存在しないため、有界な集合を誘引する最小の集合です。
存在
グローバルアトラクターは、もし存在すれば、力学系の長期的な挙動はすべてそこに引き込まれていくことがわかります。
しかしさきほど見たように、やや条件が多くて示すのが大変です。そこで、次のような定理が知られています。
力学系\((H, (S(t)))\)が散逸的ならば、そのコンパクトな吸収集合を\(B\)として、そのω極限集合\(A:=\omega (B)\)がグローバルアトラクターとなる。さらに、\(H\)が連結ならば、\(A\)も連結。
証明は:Robinson, Infinite-Dimensional Dynamical Systemsを参照してください。
例
以上の定理を用いれば、散逸系であることを示せば、そこにグローバルアトラクターが存在すると言えます。
例えば、\(\mathbb{R}^2\)において、
\[ \begin{aligned} \left\{ \begin{array}{l} \frac{dx}{dt} =-x+y \\ \frac{dy}{dt} =-x-y \end{array} \right.\end{aligned} \]
という微分方程式を考えましょう。
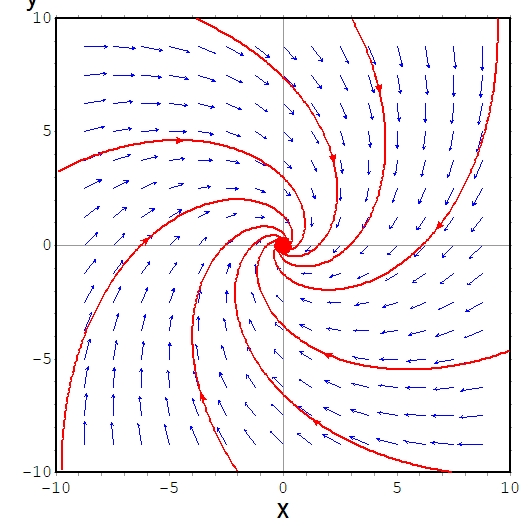
この力学系において、原点を中心とする円盤\(B_1 =\{(x_0,y_0)\mid x_0 ^2+y_0^2 \leq 1\}\)は吸収集合です。
したがってそれは散逸系で、\(A=\omega (B_1)\)がグローバルアトラクターです。特に、\(\omega (B_1) =\{(0,0)\}\)です。これは最初に示した例の2次元バージョンと言えますね。
1点集合や有限集合がアトラクターとなるとき、それは点アトラクターと呼ばれます。
\[ \begin{aligned} \begin{pmatrix} \frac{dx_1}{dt}\\ \frac{dx_2}{dt} \end{pmatrix} = \begin{pmatrix} x_2\\ -\mu(x_1^2-1)x_2-x_1 \end{pmatrix}\end{aligned} \]
では、漸近安定なω極限集合が存在し、散逸系であることが知られています。
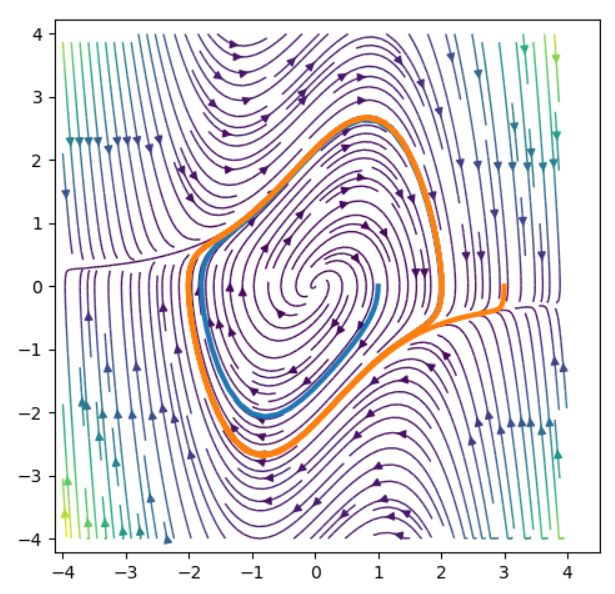
特にそのω極限集合は、閉曲線となり、それはリミットサイクルと呼ばれるものです。アトラクターが閉曲線となるとき、それは周期的アトラクター(periodic attractor)と呼ばれます。
ローレンツアトラクター
\[\left\{ \begin{array}{l} \frac{dx}{dt} = -ax +ay \\ \frac{dy}{dt} = -xz + bx -y \\ \frac{dz}{dt} = xy – cz \end{array} \right.\]
も散逸系であり、したがってグローバルアトラクターが存在します。
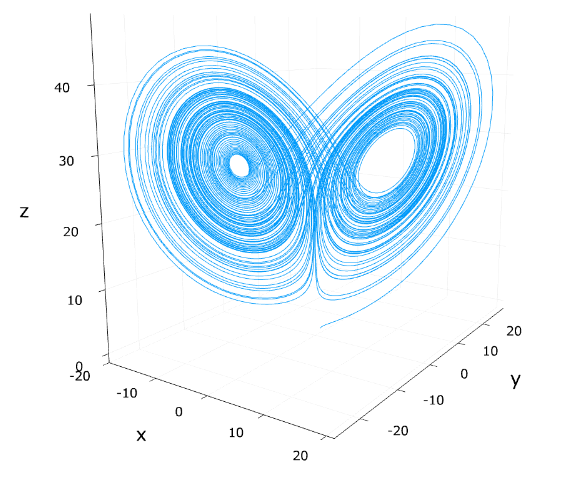
上の図は解曲線ですが、そのアトラクターは複雑な形状をしていて、ローレンツアトラクターと呼ばれています。
以上、グローバルアトラクターとは:散逸系における存在、例を紹介してきました。
周囲の状態を引き寄せる不変集合:グローバルアトラクターは、良い性質を持ちますが、その分存在を示すのが難しいです。ただしコンパクトな吸収集合が存在する:散逸系ならば、アトラクターの存在が言えるわけですね。
微分方程式の解の長期的な挙動を調べるにあたり、平衡解とその安定性だけでなく、アトラクターも調べられるとより広い範囲のことがわかって嬉しいですね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)
こちらもおすすめ
上限・下限(sup,inf)、有界とは:具体例、最大・最小値との違い
カオス理論、バタフライ・エフェクトとは何か? ローレンツ・アトラクターを例に
方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門