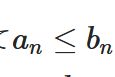集合列の極限の求め方、例、上極限と下極限

どうも、木村（@kimu3_slime）です。

広義積分やルベーグ積分、確率論を考えるときに、集合列の極限というものを考えたくなります。

今回は、その簡単な例での求め方、上極限と下極限の関係を紹介します。

前提知識：集合の要素、部分集合、等しいことの証明の書き方、集合族の扱い方（和集合・共通部分）：実数の区間を例に

集合列の極限の求め方
集合の上極限、下極限
こちらもおすすめ

集合列の極限の求め方

簡単な例としてユークリッド空間\(\mathbb{R}^N\)の部分集合の列を考えましょう。

イメージとしては、平面\(\mathbb{R}^2\)の部分集合の列だと思うと簡単です。\(B(a,r):=\{ x \in \mathbb{R}^n \mid \|x-a\| <r\}\)を開球と呼びます。

\(A_n := B(a,n) \subset \mathbb{R}^N\)とすると、\((A_n)_{n \in \mathbb{N}}\)という集合列ができます。これは半径\(n\)がどんどん大きくなっていくので、極限を取れば全体\(\mathbb{R}^N\)になってほしいですね。

集合列の極限の定義は、後に紹介するようにうまくできます。そしてその計算方法として、次の性質が使えます。

集合列\((A_n)\)が広義単調増加（すべての\(n\)に対し\(A_n \subset A_{n+1}\)）とする。このとき、集合列の極限は存在し、

\[ \begin{aligned}\lim_{n \to \infty}A_n = \bigcup_{n \in \mathbb{N}} A_n\end{aligned} \]

が成り立つ。

これを使ってみましょう。

\(B(a,n)\subset B(a,n+1)\)なので、\((A_n)\)は広義単調増加です。

そこで、集合列の和集合が\(\bigcup _{n \in \mathbb{N}}A_n = \mathbb{R}^N\)となることを確かめます。\(x\in \bigcup _{n \in \mathbb{N}}A_n\)とすると、ある\(n\)によって\(x \in A_n\)で、\(A_n \subset \mathbb{R}^N\)なので、\(x \in \mathbb{R}^N\)です。一方、\(x\in \mathbb{R}^N\)としましょう。アルキメデスの性質より、\(\|x-a\|< n\)を満たす\(n\)が存在します。つまり、\(x \in B(a,n) =A_n\)なる\(n\)が存在するので、和集合の定義から\(x \in \bigcup _{n \in \mathbb{N}}A_n\)が言えました。

よって、\(\lim_{n \to \infty }A_n = \mathbb{R}^N\)です。

別の例として、ある点を除いた集合列を考えてみましょう。

\(D_n: = \{x \in \mathbb{R}^N \mid \frac{1}{n}<\|x-a\|<r\}\)なる集合列を考えます。すると、

\[ \begin{aligned}\lim_{n \to \infty}D_n = B(a,r)\setminus\{a\}\end{aligned} \]

となることが、さきほどと同様の方法で示せます（確かめてみてください）。

上2つの例は大きくなっていく集合列でしたが、小さくなっていくケースでも同様の議論ができます。

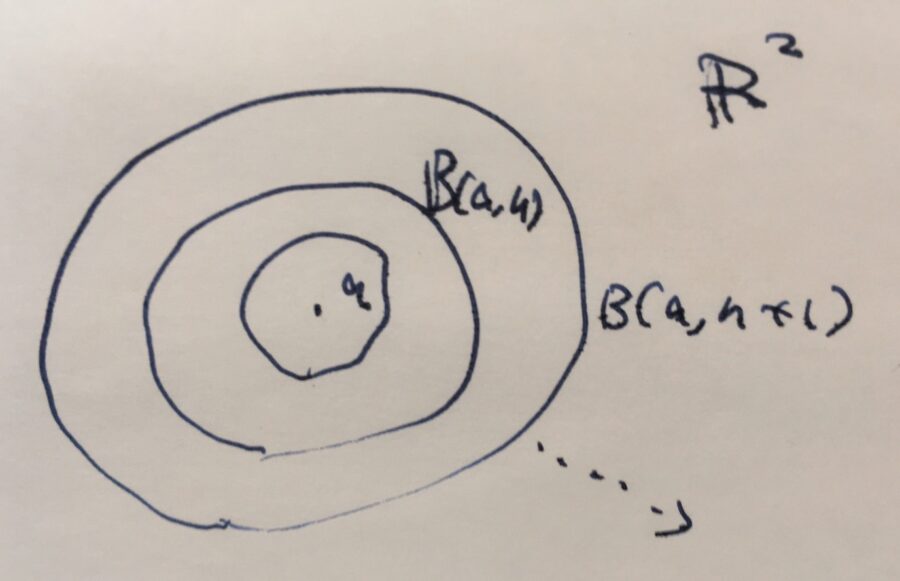
\(E_n := B(a, r+\frac{1}{n})\)としましょう。これは極限を取れば、単に閉じた球に収束しそうです。

集合列\((A_n)\)が広義単調減少（すべての\(n\)に対し\(A_n \supset A_{n+1}\)）とする。このとき、集合列の極限は存在し、

\[ \begin{aligned}\lim_{n \to \infty}A_n = \bigcap_{n \in \mathbb{N}} A_n\end{aligned} \]

が成り立つ。

これによって\((E_n)\)の極限を求めてみます。

\(B(a,r+\frac{1}{n})\supset B(a,r+\frac{1}{n+1})\)なので、\((E_n)\)は広義単調減少です。

\(\bigcap_{n \in \mathbb{N}} E_n= D(a,r)\)、\(D(a,r)=\{x \mid \|x-a\|\leq r\}\)であることを確かめましょう。\(x \in \bigcap_{n \in \mathbb{N}} E_n\)とすると、共通部分の定義から、すべての\(n \in \mathbb{N}\)に対して\(x \in B(a,r+\frac{1}{n})\)です。\(\|x-a \|> r\)と仮定すると（背理法）、アルキメデスの性質から\(\|x-a\| > r+\frac{1}{n}\)を満たす自然数\(n\)が存在します。これは共通部分の性質に矛盾するので、\(\|x-a\| \leq r\)、つまり\(x \in D(a,r)\)が言えました。一方、\(x \in D(a,r)\)とすると、すべての\(n\)に対して\(x \in D(a,r+\frac{1}{n})\)でもあります。共通部分の定義から、\(x\in\bigcap_{n \in \mathbb{N}} E_n \) と言えました。

よって、\(\lim_{n \to \infty}E_n =D(a,r)\)です。

集合の上極限、下極限

集合の極限を定義するためには、集合の上極限、下極限という考え方を使います。

\[ \begin{aligned}\limsup _{n\to \infty}A_n := \bigcap _{k \in \mathbb{N}} \bigcup_{n \in \mathbb{N}, n \geq k}A_n\end{aligned} \]

\[ \begin{aligned} \liminf _{n\to \infty}A_n :=\bigcup _{k \in \mathbb{N}} \bigcap_{n \in \mathbb{N}, n \geq k}A_n\end{aligned} \]

と定義される集合を、集合列の\((A_n)\)の上極限（じょうきょくげん limit superior）、下極限（かきょくげん limit inferior）と呼びます。

幾何学的なイメージから、外極限（outer limit）、内極限（innner limit）とも呼ばれます。

この定義は、数列の上極限・下極限にヒントを得たものです。

\[ \begin{aligned}\limsup_{n\to \infty} a_n := \inf_{k \in \mathbb{N}} \sup_{n \in \mathbb{N}, n \geq k} a_n\end{aligned} \]

\[ \begin{aligned}\liminf_{n\to \infty} a_n := \sup_{k \in \mathbb{N}} \inf_{n\in \mathbb{N}, n \geq k} a_n\end{aligned} \]

\(\sup\)が\(\bigcup\)に、\(\inf\)が\(\bigcap\)に対応していますね。

数列については、

収束すること：\(\lim_{n\to \infty}a_n =a\)
上極限・下極限が一致すること：\(\limsup_{n\to \infty}a_n = \liminf_{n \to \infty}a_n\)

が同値になります。

そこでこの性質になぞらえて、集合列\((A_n)\)が収束することを、上極限と下極限が一致すること

\[ \begin{aligned}\limsup_{n\to \infty}A_n = \liminf_{n \to \infty}A_n\end{aligned} \]

と定義しましょう。これを集合論的な極限（set-theoretic limit）と呼びます。

（一般には、集合間の距離を使った位相的な極限とは別物です。）

すると、集合列が広義単調増加なときは、

\[ \begin{aligned}\liminf_{n\to \infty}A_n = \limsup_{n \to \infty}A_n\\ =\bigcup_{n \in \mathbb{N}, n \geq 1}A_n \end{aligned} \]

となり、集合列は収束して

\[ \begin{aligned}\lim_{n \to \infty}A_n = \bigcup_{n \in \mathbb{N}} A_n\end{aligned} \]

となります。

これを確かめてみましょう。

\(\limsup_{n \to \infty}A_n =\bigcup_{n \in \mathbb{N}, n \geq 1}A_n\)について。

\(x\in \limsup_{n \to \infty}A_n\)とすると、すべての\(k \in \mathbb{N}\)に対し、\(x\in \bigcup_{n \in \mathbb{N}, n \geq k}A_n\)です。特に\(k=1\)のときを考えれば、\(x\in \bigcup_{n \in \mathbb{N}, n \geq 1}A_n\)です。
一方、\(x\in \bigcup_{n \in \mathbb{N}, n \geq 1}A_n\)としましょう。\(k \in \mathbb{N}\)を任意とします。\(x\in \bigcup_{n \in \mathbb{N}, n \geq 1}A_n\)より、ある\(n\)によって\(x \in A_n\)です。\(N:= \max\{n,k\}\)とすると、集合列の単調性から\(A_n \subset A_N\)で、\(x\in A_N\)です。ここで\(N \geq k\)なので、\(x\in \bigcup_{n \in \mathbb{N}, n \geq k}A_n\)です。\(k\)は任意だったので、\(x\in \bigcap _{k \in \mathbb{N}} \bigcup_{n \in \mathbb{N}, n \geq k}A_n\)が言えました。

\(\liminf_{n \to \infty}A_n =\bigcup_{n \in \mathbb{N}, n \geq 1}A_n\)について。

\(x\in \liminf_{n \to \infty}A_n\)とすると、ある\(k \in \mathbb{N}\)に対し、\(x\in \bigcap_{n \in \mathbb{N}, n \geq k}A_n\)です。共通部分の定義から、特に\(x\in A_k\)です。したがって、\(x \in \bigcup_{n \in \mathbb{N}, n \geq 1}A_n\)と言えました。
一方、\(\bigcup_{n \in \mathbb{N}, n \geq 1}A_n\)とします。和集合の定義から、ある\(k\)によって\(x \in A_k\)です。集合列の単調性から、すべての\(n, n\geq k\)に対し、\(A_k \subset A_n\)で、\(x \in A_n\)です。つまり、\(x\in\bigcap_{n \in \mathbb{N}, n \geq k}A_n\)。このような\(k\)が存在するので、\(x\in \bigcup _{k \in \mathbb{N}} \bigcap_{n \in \mathbb{N}, n \geq k}A_n\)と言えました。

広義単調減少な集合列についても、同様の事実が証明できます。

すべての数列が収束するわけではないように、集合列にも収束しないものが存在します。

\(a_n=(-1)^n\)とすると、

\[ \begin{aligned}\limsup_{n\to \infty} a_n =1\end{aligned} \]

\[ \begin{aligned}\liminf_{n\to \infty} a_n =-1\end{aligned} \]

となって、上極限・下極限が一致せず、収束しません。

これと同様に、集合列\(A_n :=B(a,2+(-1)^n)\)について考えましょう。すると、

\[ \begin{aligned}\limsup_{n\to \infty} A_n =B(a,3)\end{aligned} \]

\[ \begin{aligned}\liminf_{n\to \infty} A_n =B(a,1)\end{aligned} \]

となります。

なぜか。\(k \)を任意として、

\[ \begin{aligned}\bigcup _{n \geq k} A_n = B(a,3)\end{aligned} \]