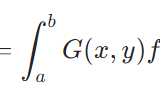可逆作用素、逆作用素とは：定義、例を解説

どうも、木村（@kimu3_slime）です。

今回は、可逆作用素、逆作用素の定義、例を紹介します。

導入
逆作用素の定義
例
- 行列と逆行列
- 微分作用素と積分作用素
こちらもおすすめ

導入

ラプラス方程式や熱方程式などの偏微分方程式の問題において、ラプラシアン\(-\Delta\)の固有値や固有関数は重要です。

ただしラプラシアンは一般に非有界な作用素であり、コンパクトな対称作用素が持つ固有値の性質（ヒルベルト・シュミットの定理）がそのままでは利用できません。

しかし、ラプラシアンは逆作用素というものを考えることで、それがコンパクトな対称作用素となることを通じて、固有値や固有関数を調べることができます。

逆作用素の定義

では、逆作用素について考えていきましょう。

\(X,Y\)をノルム空間、\(F:D(F) \to Y\)を線形作用素とします。\(X\)の部分空間\(D(F)\)は\(F\)の定義域（domain）と呼び、必ずしも\(X\)全体でなくて良いものとしましょう。

\(F\)が可逆作用素（invertible operator）であるとは、\(F\)が\(D(F)\)において単射であること、すなわち「\(u_1,u_2 \in D(F), u_1 \neq u_2\)ならば\(F(u_1)\neq F(u_2)\)となること」です。

核の言葉を使えば、これは\(\ker F =\{0\}\)と同値です（定義域が\(D(F)\)であることに注意：\(\ker F:=\{u \in D(F) \mid F(u)=0\}\)）。

単射の定義の対偶を考えれば、「すべての\(v \in R(F)\)に対し、\(u \in D(F)\)を変数とする方程式\(F(u) =v\)は一意な解を持つ」と言い換えられます。ここで\(R(F)=\mathrm{Im}(F)\)は\(F\)の値域（range）、像です。

\(F\)が可逆であるとき、\(F^{-1}:R(F)\to D(F)\)を\(F^{-1}(v)=u\)（\(v\)に対し、\(F(u)=v\)の解\(u\)を対応させる）によって定義できます。この作用素\(F^{-1}\)が逆作用素（inverse operator）です。

\(F\)が可逆で、\(F^{-1}\)が\(F\)の逆作用素であることは、

すべての\(v \in R(F)\)に対し、\(F(F^{-1}(v))=v\)
すべての\(u \in D(F)\)に対し、\(F^{-1}(F(u))=u\)

の2つを満たす作用素\(F^{-1}\)が存在すること同値です。これを証明しましょう。

まず、\(F\)が可逆で、\(F^{-1}\)を\(F\)の逆作用素とします。\(v \in R(F)\)に対し、\(F\)が可逆であることから、\(F(u)=v\)、\(F^{-1}(v)=u\)を満たす\(u \in D(F)\)が存在します。したがって、これらを組み合わせれば\(F(F^{-1}(v))=F(u)=v\)です。また、\(u \in D(F)\)に対し、\(F(u)=F(u), F(u) \in R(F)\)なので、逆作用素の定義から\(F^{-1}(F(u))=u\)です。

逆に、2つの条件を満たす作用素\(F^{-1}\)が存在したとしましょう。\(v \in R(F)\)に対し、方程式\(F(u)=v\)は、\(u=F^{-1}(v)\)という解を持ちます。\(F(F^{-1}(v))=v\)が成り立っているからです。その解が一意であることを示すために、\(F(u_1)=F(u_2) =v\)と仮定しましょう。\(F^{-1}\)を作用させると、前者の条件から\(u_1 =F^{-1}(F(u_1))=F^{-1}(F(u_2))=u_2\)となるので、一意性が示せました。よって\(F\)は可逆です。さらに、\(u:=F^{-1}(v)\)と置くと、\(F(F^{-1}v)=v\)からそれは\(F(u)=v\)の解となるので、\(F^{-1}\)は逆作用素です。

（ちなみに、逆作用素は存在すれば一意です。）

例

行列と逆行列

\(A\)を\(N\)次の正方行列、特に可逆行列としましょう。行列が可逆であることと単射であることは同値なので、\(A\)は可逆な作用素です。定義域、値域はともに\(D(A)=R(A)=\mathbb{R}^N\)です。

逆行列\(A^{-1}\)が\(A\)の逆作用素です。実際、逆行列の定義から\(AA^{-1}=A^{-1}A=I\)を満たします。これはさきほどの条件

すべての\(v \in R(F)\)に対し、\(F(F^{-1}(v))=v\)
すべての\(u \in D(F)\)に対し、\(F^{-1}(F(u))=u\)

と同値です。したがって、\(A^{-1}\)は逆作用素です。

微分作用素と積分作用素

\(\Omega =[0,1] \subset \mathbb{R}\)として、\(F:L^{2}(\Omega)\to L^2(\Omega)\)を\([F(u)](x) =\frac{du}{dx}(x)\)という単純な微分作用素を考えましょう。ただし定義域は微分可能であるように、\(D(F)=\{ u \in C^{1}(\Omega) \mid u(0)=0\}\)とします。

さて、この作用素は可逆でしょうか？　可逆だとしたら、逆作用素は何でしょうか。

微分と積分は逆関係、微分積分学の基本定理を思い出すと判定できるでしょう。\(F^{-1}:R(F)\to D(F)\)を

\[[F^{-1}(v)](x): = \int_0^x v(y)dy\]

によって定めます。微積分学の基本定理より、

\[\begin{aligned} &F( F^{-1}(v))(x)\\ &= \frac{d}{dx} \int_0^x v(y)dy \\ &= v(x)\end{aligned}\]

\[\begin{aligned} &F^{-1}( F(u))(x)\\ &= \int_0^x \frac{du}{dy}(y)dy \\ &=[u(y)]_{y=0}^{y=x} \\&=u(x)\end{aligned}\]

となるので、\(F\)は可逆で、積分作用素\(F^{-1}\)が逆作用素となることが示せました。

微分作用素は\(L^2\)ノルムで非有界でした。この例は、非有界な作用素の逆作用素は有界となりうることを示しています。

逆に見れば、積分作用素の逆作用素は微分作用素です。したがって、有界作用素の逆作用素は有界作用素とは限りません。

以上、可逆作用素、逆作用素の定義、例を紹介してきました。

\(F\)が対称であったり非有界であっても、条件を課せば逆作用素\(F^{-1}\)は対称で有界な作用素になるという良い性質を持ちます。これについては別記事にて。

木村すらいむ（@kimu3_slime）でした。ではでは。