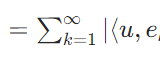どうも、木村(@kimu3_slime)です。
今回は、可分な空間とは、ヒルベルト空間において完全正規直交系の存在と同値であることの証明を紹介します。
可分な空間
\(X\)をノルム空間とします。\(X\)が可分である(separable)とは、多くても可算な濃度の部分集合\(A\)で、閉包が全体に一致する\(\overline{A}=X\)(\(A\)は\(X\)において稠密)ようなものが存在することです。
例えば、ユークリッド空間\(\mathbb{R}^N\)は可分です。有理数の集合\(A=\mathbb{Q}^N\)を選べば、それらは可算で、かつ稠密であることが知られています。
複素数\(\mathbb{C}\)も\(z=x+yi, x,y \in \mathbb{R}\)と表せるので、\(\{z \mid z=x+yi ,x,y\in \mathbb{Q}\}\)により可分です。
可分な空間においては、どんな要素\(x \in X\)も、ある決まった可算集合\(A\)の点列\(a_n\)によって、近似することができます\(a_n \to x\)。ラフな言い方ですが、「可算の基底のようなものが存在するかどうか」と言えるでしょう。
可分という性質は、主に関数空間の議論で重要です。ここでは知られた性質を紹介しておきましょう。
- \(L^p\)、\(\ell^p\)、\(W^{k,p}\)(\(1 \leq p<\infty\))は可分である。
- \(C(K)\)(\(K\)はコンパクトな距離空間)は可分である。
- \(L^\infty\)、\(\ell^\infty\)(\(1 \leq p<\infty\))は可分でない。
ヒルベルト空間において完全正規直交系の存在と同値であることの証明
\(X\)がヒルベルト空間のとき、可分な空間はわかりやすい特徴づけを持ちます。
\(H\)をヒルベルト空間とします。\(H\)が可分であることは、\(H\)に可算な完全正規直交系が存在することと同値です。
これを証明しましょう。
可分ならば直交系の存在
\(H\)を可分な空間とし、可算で稠密な集合を\(A=(a_n)_n\)としましょう。
\(n\)を自然数とします。\(a_n\)が\(a_1,\dots,a_{n-1}\)の線形結合であるときは、それを取り除いておくことにしましょう。それにより、\(a_1,\dots,a_n\)を線形独立なベクトルとできます。グラム・シュミットの直交化法により、正規直交系\((c_n)_n\)が作り出せます。
\[ \begin{aligned}b_1 :=a_1\end{aligned} \]
\[ \begin{aligned}c_1 := \frac{1}{\|b_1\|}b_1\end{aligned} \]
\[ \begin{aligned}b_2 =a_2 -\langle c_1,a_2 \rangle c_1\end{aligned} \]
\[ \begin{aligned}c_2 =\frac{1}{\|b_2\|} b_2\end{aligned} \]
\[ \begin{aligned}b_k =a_k – \sum_{i=1}^{k-1}\langle c_i,a_k \rangle c_i \end{aligned} \]
\[ \begin{aligned}c_k = \frac{1}{\|b_k\|}b_k\end{aligned} \]
\(A=(a_n)_n\)から\((c_n)_n\)にするとき、取り除いた要素はありますが、それらは\((c_n)_n\)の線形結合として表せます。したがって、直交補空間は一致\(A^{\perp}=C^{\perp}\)して、\(A\)が完全正規直交系であることと\(A^{\perp}=\{0\}\)は同値なので、\(C^{\perp}=\{0\}\)です。\(C\)は正規直交系なので、再び同値性を用いれば、\(C^{\perp}=\{0\}\)から\(C=(c_n)_n\)が完全正規直交系であることが言えました。
直交系が存在するならば可分
\(E=(e_n)_n\)を可算な完全正規直交系としましょう。すべての\(u \in H\)に対し、\(u = \sum_{k=1}^\infty\langle u,e_k\rangle_H e_k\)と表せます。
\(A_n =\{u \in H \mid \sum_{k=1}^n c_n e_n , c_n \in \mathbb{Q}\}\)とし、それらの和集合を\(A= \bigcup_{n\in \mathbb{N}} A_n\)としましょう(係数体を\(\mathbb{R}\)としていますが、\(\mathbb{C}\)でも同様です)。\(\mathbb{Q}\)は可算なので、その有限個の線形結合である\(A_n\)は可算です。可算な集合の和集合は可算なので、\(A\)は可算です。
したがって、\(\overline{A}=H\)となることを示せば、\(H\)は可分です。
\(u \in H\)とし、それが\(v_n \in A\)により\(\lim_{n \to \infty} v_n =u\)と表せることを示しましょう。有限項を有理係数で近似し、それ以降は小さな項となるという流れで示します。
\(\varepsilon >0\)とします。完全正規直交系であることから、\(u = \sum_{k=1}^\infty\langle u,e_k\rangle_H e_k\)と展開できます。右辺の級数は収束するので、\(\lim_{n \to \infty}\sum_{k=n}^\infty\langle u,e_k\rangle_H e_k=0\)です。したがって、「\(\|\sum_{k=N+1}^\infty\langle u,e_k\rangle_H e_k\|<\frac{\varepsilon}{2}\)」を満たす\(N\)が存在します。
また、\(\mathbb{R}\)において\(\mathbb{Q}\)が稠密であることから、各\(k\)に対して、\(|\langle u,e_k\rangle_H-c_k|< \frac{\varepsilon}{2^{k+1}}\)を満たす\(c_k \in \mathbb{Q}\)が存在します。
そこで\(u_n := \sum_{k=1}^n c_k e_k\)と置きましょう。これは有理係数の線形結合なので、\(u_n \in A\)です。また、その差を評価すれば、\(n \geq N\)のとき、三角不等式、\((e_k)\)が正規であること、等比級数の公式から、
\[\begin{aligned} &\|u-u_n\|_H \\ &=\|\sum_{k=1}^\infty\langle u,e_k\rangle_H e_k- \sum_{k=1}^n c_k e_k\| \\ &=\|\sum_{k=1}^n(\langle u,e_k\rangle_H-c_k) e_k+\sum_{k=n+1}^\infty\langle u,e_k\rangle_H e_k\|_H\\ &\leq \|\sum_{k=1}^n(\langle u,e_k\rangle_H-c_k) e_k\|_H+\|\sum_{k=n+1}^\infty\langle u,e_k\rangle_H e_k\|_H \\ &\leq \sum_{k=1}^n|\langle u,e_k\rangle_H-c_k| +\|\sum_{k=N+1}^\infty\langle u,e_k\rangle_H e_k\|_H \\ &< \sum_{k=1}^n\frac{\varepsilon}{2^{k+1}}+ \frac{\varepsilon}{2} \\ & \leq \sum_{k=1}^\infty \frac{\varepsilon}{2^{k+1}}+ \frac{\varepsilon}{2}\\&= \frac{\varepsilon}{2^2} \frac{1}{1-\frac{1}{2}}+ \frac{\varepsilon}{2} \\ &= \varepsilon \end{aligned}\]
となるので、\(u_n \to u\)です。よって、\(H\)は可分であることが示せました。
以上、可分な空間とは、ヒルベルト空間において完全正規直交系の存在と同値であることの証明を紹介してきました。
この結果は、「可分な無限次元ヒルベルト空間は、\(\ell^2\)とヒルベルト空間として同型である」というまとめを導くことが知られています。
僕は最初に学んだとき、可分な空間の意義やイメージがつかみにくかったです。少なくともヒルベルト空間においては、それは可算な完全正規直交系(基底)があることと同値と知ると、その一般化として(ヒルベルト空間とは限らない)可分な空間という用語があると理解できますね。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)
こちらもおすすめ
無限集合の濃度とは? 写像の全単射、可算無限、カントールの対角線論法
連続関数、可積分関数の線形空間(関数空間)、微分と積分の線形性とは