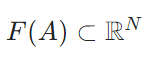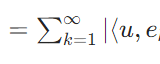ヒルベルト・シュミット積分作用素がコンパクト作用素であることの証明

どうも、木村（@kimu3_slime）です。

今回は、ヒルベルト・シュミット積分作用素がコンパクト作用素であることの証明を紹介します。

証明
こちらもおすすめ

証明

方針と完全正規直交系

\(\Omega \subset \mathbb{R}^N\)を開集合、核を\(k (x,y) \in L^2(\Omega \times \Omega)\)とし、ヒルベルト・シュミット積分作用素\(K: L^2(\Omega) \to L^2(\Omega)\)を

\[[K(u)](x): = \int_{\Omega}k(x,y)u(y)dy\]

考えましょう。

\(K\)がコンパクト作用素であることを示すために、コンパクト作用素のなす空間\(B_c(L^2(\Omega),L^2(\Omega))\)が閉集合であることを利用し、\(K\)を近似するコンパクト作用素\(K_n\)を構成する、という方針です。

\(L^2(\Omega)\)は可分なヒルベルト空間（完備な内積空間）で、完全正規直交系\((\phi_\ell)_{\ell}\)が存在することが知られています。さらに、それらの積によってできる関数系\((\phi_i(x)\phi_j(y))_{i,j}\)は\(L^2(\Omega \times \Omega)\)の完全正規直交系となります。

したがって、\(k\in L^2(\Omega \times \Omega)\)を

\[\begin{aligned} k(x,y)=\sum_{i,j=1}^\infty k_{i,j} \phi_i(x)\phi_{j}(y) \end{aligned}\]

と展開できます（完全性）。

コンパクトな近似作用素列の構成

そこでその一部分を使って、\(K_n:L^2(\Omega)\to L^2(\Omega)\)を

\[k_n (x,y):=\sum_{i,j=1}^n k_{i,j} \phi_i(x)\phi_{j}(y)\]

\[[K_n(u)](x):= \int_{\Omega} k_n(x,y)u(y)dy\]

と定義しましょう。

値が\(L^2(\Omega)\)となることを確かめるために、\(k_n\)を評価します。一般に、完全正規直交系であることと、パーセバルの等式が成り立つことは同値なので、

\[\begin{aligned} &\|k\|_{L^2(\Omega \times \Omega)}^2 \\ &= \int_{\Omega \times \Omega}|k(x,y)|^2 dxdy \\ &= \sum_{i,j=1}^\infty |k_{i,j}|^2 \end{aligned}\]

となり、\(k\in L^2(\Omega \times \Omega)\)だからこの値は有限です。したがって、コーシー・シュワルツの不等式より

\[\begin{aligned} &\|K_n(u)\|_{L^2(\Omega)}^2\\ &=\int_{\Omega}|\int_{\Omega} k_n(x,y)u(y)dy|^2 dx \\&=\int_{\Omega}|\langle k_n(x,\cdot),u \rangle_{L^2(\Omega)}|^2 dx \\ &\leq \int_{\Omega}\|k_n(x,\cdot)\|_{L^2(\Omega)}^2 \|u\|_{L^2(\Omega)}^2 dx \\ &= \|u\|_{L^2(\Omega)}^2 \int_{\Omega \times \Omega}|k_n(x,y)|^2 dxdy \\ & \leq \|u\|_{L^2(\Omega)}^2 \|k\|_{L^2(\Omega \times \Omega)}^2 \\ & < \infty \end{aligned}\]

となるので、\(K_n(u) \in L^2(\Omega)\)です。

また、積分の線形性より、\(u,v \in L^2(\Omega)\)、\(\lambda\)をスカラーとして

\[\begin{aligned} &[K_n(\lambda u+v)](x) \\ &= \int_{\Omega} k_n(x,y)(\lambda u(y)+v(y))dy\\&= \lambda \int_{\Omega} k_n(x,y)u(y)dy+\int_{\Omega} k_n(x,y)v(y)dy \\&= \lambda [K_n(u)](x)+[K_n(v)](x) \end{aligned}\]

となるので、\(K_n\)は線形作用素です。

さらに、コンパクト作用素であることを示しましょう。\(u \in L^2(\Omega)\)を\(u=\sum_{\ell=1}^\infty c_{\ell} \phi_{\ell}\)と表すと、\((\phi_\ell)_{\ell}\)が正規直交系であることに注意して、

\[\begin{aligned} & [K_n(u)](x)\\ &= \int_{\Omega}k_n(x,y)u(y)dy \\ &=\int_{\Omega}\sum_{i,j=1}^n k_{i,j} \phi_i(x)\phi_{j}(y) \sum_{\ell=1}^\infty c_{\ell} \phi_{\ell}(y)dy\\ &= \langle \sum_{i,j=1}^n k_{i,j} \phi_i(x)\phi_{j},\sum_{\ell=1}^\infty c_{\ell} \phi_{\ell} \rangle_{L^2(\Omega)}\\ &= \langle \sum_{i,j=1}^n k_{i,j} \phi_i(x)\phi_{j}, c_{j} \phi_{j} \rangle_{L^2(\Omega)}\\ &= \sum_{i,j=1}^n k_{i,j} c_{j} \phi_i(x) \langle\phi_{j}, \phi_{j} \rangle_{L^2(\Omega)} \\ &=\sum_{i,j=1}^n k_{i,j} c_{j} \phi_i(x) \end{aligned}\]

となります。したがって\(K_n\)による像は有限次元で、有限ランク作用素となり、コンパクト作用素です。

近似の正当性

\(K_n\)が\(K\)に作用素ノルムで収束することを示しましょう。

コーシー・シュワルツの不等式より

\[\begin{aligned} &\|(K-K_n)(u)\|_{L^2(\Omega)}^2 \\ &=\int_{\Omega} |\int_{\Omega}(k(x,y)-k_n(x,y))u(y)dy|^2 dx \\&= \int_{\Omega} |\langle k(x,\cdot)-k_n(x,\cdot), u \rangle_{L^2(\Omega)}|^2 dx\\ &\int_{\Omega} \| k(x,\cdot)-k_n(x,\cdot)\|_{L^2(\Omega)}^2 \|u \|_{L^2(\Omega)}^2 dx \\&= [\int_{\Omega\times \Omega}|k(x,y)-k_n(x,y)|^2dxdy] \|u \|_{L^2(\Omega)}^2\end{aligned}\]

となるので、作用素ノルムの定義から\(\|K-K_n\|_{B(L^2(\Omega),L^2(\Omega))}^2 \leq \int_{\Omega\times \Omega}|k(x,y)-k_n(x,y)|^2dxdy \)です。さらにこれを評価すれば、パーセバルの等式から

\[\begin{aligned} &\|K-K_n\|_{B(L^2(\Omega),L^2(\Omega))}^2 \\ &\leq \int_{\Omega\times \Omega}|k(x,y)-k_n(x,y)|^2dxdy \\ &= \int_{\Omega\times \Omega} |\sum_{i,j=1}^\infty k_{i,j} \phi_i(x)\phi_{j}(y)-\sum_{i,j=1}^n k_{i,j} \phi_i(x)\phi_{j}(y)|^2dxdy \\ &= \int_{\Omega\times \Omega} |\sum_{i,j=n+1}^\infty k_{i,j} \phi_i(x)\phi_{j}(y)|^2dxdy \\ &\leq \int_{\Omega\times \Omega} |\sum_{i,j=1}^\infty k_{i,j} \phi_i(x)\phi_{j}(y)|^2dxdy \\ &= \sum_{i,j=n+1}^\infty |k_{i,j}|^2 \end{aligned}\]

となります。

一般に、\(\sum_{\ell=1}^\infty a_\ell <\infty\)ならば、\(\lim_{n\to \infty}\sum_{\ell=n+1}^\infty a_\ell =0\)です。\(\varepsilon>0\)とします。級数の収束から、「\(n \geq N\)ならば\(|\sum_{\ell=1}^n a_\ell-\sum_{\ell=1}^\infty a_\ell|<\varepsilon\)」を満たす\(N\)が存在します。ここで差は\(|\sum_{\ell=n+1}^\infty a_\ell|=|\sum_{\ell=1}^n a_\ell-\sum_{\ell=1}^\infty a_\ell|<\varepsilon\)なので、\(\lim_{n\to \infty}\sum_{\ell=n+1}^\infty a_\ell =0\)となりました。

\(k\in L^2(\Omega \times \Omega)\)より\(\sum_{i,j=1}^\infty |k_{i,j}|^2< \infty\)だったので、\(\lim_{n\to \infty}\|K-K_n\|_{B(L^2(\Omega),L^2(\Omega))}=0\)が言えました。

コンパクト作用素のなす空間\(B_c(X,Y)\)は作用素ノルムについて閉部分空間であり、\(K_n \in B_c(L^2(\Omega),L^2(\Omega))\)なので、極限も\(K \in B_c(L^2(\Omega),L^2(\Omega))\)です。よって、\(K\)がコンパクト作用素であることが示せました。

以上、ヒルベルト・シュミット積分作用素がコンパクト作用素であることの証明を紹介してきました。

コンパクト作用素の近似列が作れれば、極限としてコンパクト作用素であることが示せる流れですね。

ヒルベルト・シュミット作用素は、ストゥルム・リウビル型微分方程式の固有値問題に応用できますが、それについては別の記事にて。

木村すらいむ（@kimu3_slime）でした。ではでは。