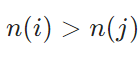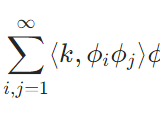どうも、木村(@kimu3_slime)です。
今回は、コンパクト作用素が有界作用素のなす空間の閉部分空間であることの証明を紹介します。
記号と主張の確認
\(X,Y\)をノルム空間、\(B(X,Y)\)を有界線形作用素のなすノルム空間(ノルムは作用素ノルム)、\(B_c(X,Y)\)をコンパクト作用素のなす部分空間とします。
\(Y\)が完備(バナッハ空間)のとき、\(B_c(X,Y)\)は閉集合(閉部分空間)になります。
一般に、完備な距離空間の閉集合は完備であり、\(Y\)が完備ならば\(B(X,Y)\)も完備なので、\(B_c(X,Y)\)は完備である(バナッハ空間)と言えます。
証明
では、\(B_c(X,Y)\)が閉集合であること、\((F_n)_n\)が\(B_c(X,Y)\)の点列で\(\lim_{n \to \infty}\|F_n-F\|_{B(X,Y)}=0, F \in B(X,Y)\)とするならば、\(F \in B_c (X,Y)\)となることを示しましょう。
\(F\)がコンパクト作用素であることを示すために、\((u_n)_n\)を\(X\)の有界な点列、\(\|u_n\| \leq R\)としましょう。\((F(u_n))\)が収束する部分列を持つことを示せばよく、そこで\(Y\)の完備性が使えそうです。つまり、コーシー列であるような部分列\((F(v_k))\)を探せば良いです。
\((u_n)_n\)が有界な点列で、\(F_1\)がコンパクトであることから、\((F_1(u_n))\)は収束する部分列を持ちます。それを\((F_1(u_{1,k}))_k\)としましょう。\((u_{1,k})\)は\((u_n)_n\)の部分列なので有界で、これに対して\(F_2\)がコンパクトであることから、\((F_2(u_{1,k}))_k\)の部分列を\((F_2(u_{2,k}))_k\)とします。これを繰り返せば(数学的帰納法)、\(\ell\)を自然数として、部分列\((F_\ell (u_{\ell,k}))_k\)は、\(\ell \leq k\)ならば収束するようなものです。
そこでこの部分列の列から、「対角成分」を取り出して\(v_k := u_{k,k}\)に注目しましょう(対角線論法)。これは\((u_n)\)の部分列です。
\((F(v_k))_k\)が\(Y\)のコーシー列であることを示しましょう。ノルムの三角不等式を用いて分割して評価してみると、
\[\begin{aligned} &\|F(v_i)-F(v_j)\|_Y \\ &\leq \|F(v_i)-F_n(v_i)\|_Y+\|F_n(v_i)-F_n(v_j)\|_Y + \|F_n (v_j)-F(v_j)\|_Y \end{aligned}\]
となります。これらは小さくなりそうです。
\(\varepsilon >0\)とします。作用素ノルムの同値な定義のひとつから、\(\lim_{n\to \infty} \sup_{\|u\|_X=1}\|F_n(u)-F(u)\|_Y =0\)です。したがって、「\(n \geq N_1\)ならば\( \sup_{\|u\|_X=1}\|F_n(u)-F(u)\|_Y<\frac{\varepsilon}{3R}\)」を満たす\(N_1\)が存在します。\(F,F_n\)が線形、ノルムの同次性、\((v_k)\)が有界(\(u_n\)が有界)、上限が上界であることから
\[\begin{aligned} &\|F(v_i)-F_n(v_i)\|_Y \\ &=\|v_i\|_X \|F(\frac{1}{\|v_i\|_X}v_i) -F_n(\frac{1}{\|v_i\|_X}v_i)\|_Y \\& \leq R \frac{\varepsilon}{3R} \\&= \frac{\varepsilon}{3}\end{aligned}\]
です。\(\|v_i\|\)で割り算しましたが、\(v_i=0\)のときでも\(F,F_n\)の線形性から\(F(v_i)-F_n(v_i)=0\)となり、ノルムの正定値性から同じ評価が成り立ちます。
この評価は番号\(i\)によらず、したがって\(v_j\)についても成り立ちます。
また、\((F_{N_1}(v_k))_k\)は、部分列の構成の仕方から\(Y\)の収束列です。収束列はコーシー列なので、「\(i,j \geq N\)ならば\(\|F_{N_1} (v_i)-F_{N_1}(v_j)\|_Y<\frac{\varepsilon}{3}\)」を満たす\(N\)が存在します。
よって、\(i,j \geq N\)ならば、ここまでの評価をまとめて、
\[\begin{aligned} &\|F(v_i)-F(v_j)\|_Y \\ &\leq \|F(v_i)-F_{N_1}(v_i)\|_Y+\|F_{N_1}(v_i)-F_{N_1}(v_j)\|_Y + \|F_{N_1} (v_j)-F(v_j)\|_Y \\ &< \frac{\varepsilon}{3}+\frac{\varepsilon}{3}+\frac{\varepsilon}{3} \\&= \varepsilon\end{aligned}\]
となるので、\((F(v_k))_k\)は\(Y\)のコーシー列です。\(Y\)は完備なので、それは収束します。
以上をまとめれば、\((F(u_n))\)は収束する部分列を持ちます。すなわち\(F\)はコンパクトで、\(F \in B_c(X,Y)\)です。これで\(B_c(X,Y)\)が\(B(X,Y)\)の閉集合であることが示せました。
以上、コンパクト作用素が有界作用素のなす空間の閉部分空間であることの証明を紹介してきました。
作用素の列、関数列の収束に関する議論としては、アルツェラ・アスコリの定理の証明でも対角線論法を用います。
今回の結果は、ある作用素\(F\)がコンパクトであることを示すには、それをコンパクト作用素の列で\((F_n)\)で近似すれば良い、というものです。これを用いてヒルベルト・シュミット作用素がコンパクトであることが示せますが、それは別記事にて。
木村すらいむ(@kimu3_slime)でした。ではでは。
Evans, Lawrence C.(著)
¥16,299 (2022-08-19時点)
こちらもおすすめ
有界線形作用素のなす集合B(X,Y)が線形空間となることの証明
有界線形作用素のなす空間B(X,Y)がノルム空間となることの証明
コンパクト作用素のなす集合が有界作用素のなす空間B(X,Y)の部分空間となることの証明
有界線形作用素のなす空間B(X,Y)がバナッハ空間となることの証明
無限集合の濃度とは? 写像の全単射、可算無限、カントールの対角線論法