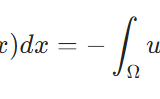テスト関数C_c^∞、関数の台とは：簡単な例

どうも、木村（@kimu3_slime）です。

今回は、テスト関数、関数の台とは何か、簡単な例を通じて紹介します。

テスト関数、関数の台とは

偏微分方程式の分野においては、連続でなく一般的な意味では微分できないような関数に対しても定義できる、一般化された微分：弱微分というものを考えます。弱微分の議論では、まずテスト関数という相方の理解が必要になるので、それを説明しましょう。

テスト関数とは、おおざっぱに言えば、有限な部分だけで値を持ち、それ以外の部分で0となっているような、なめらかな関数です。「有限な部分」という言葉は、関数の台（support サポート）によって定義されます。

\(\Omega \)を\(\subset \mathbb{R}^N\)の開集合とし、関数\(\phi : \Omega \to \mathbb{R}\)について考えましょう。

関数\(\phi\)の台とは、

\[\mathrm{supp }\, \phi:= \overline {\{x\in \Omega \mid \phi(x) \neq 0\}} \]

によって定義される、関数の定義域の部分集合です。集合の上側にある線は、\(\Omega\)における閉包です。

難しいかもしれないので、具体例を通じて考えましょう。

\(\Omega =\mathbb{R}\)とし、次の図のような関数を考えます。

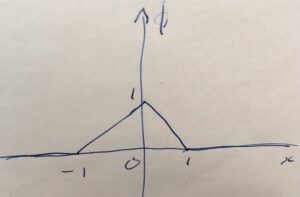
\(x \leq -1, 1 \leq x\)では0の値を取り、原点付近だけ0でない値を取る関数ですね。この関数\(\phi\)の台を求めてみましょう。

まず、\(\phi(x) \neq 0\)となるのはどこでしょうか。区間で言えば、\(-1<x <1\)ですね。したがって、

\[{\{x\in \Omega \mid \phi(x) \neq 0\}}=(-1,1) \]

という開区間になります。その閉包、つまりこの開区間を含む最小の閉集合は、端点を含めた閉区間\([-1,1]\)です。よって、

\[\mathrm{supp }\, \phi = [-1,1] \]

となることがわかりました。台が定義域の0でない部分を示す閉集合であることが、この例で感じられたでしょうか。

（細かい話になりますが、台では\(\Omega\)における閉包を考えるので、\(\mathbb{R}^N\)における閉集合になるとは限りません。その話の理解には、相対位相への理解が必要です。）

上の例は、「有限な台」を持つ関数の例です。\([-1,1]\)は\(\mathbb{R}\)の有界な閉集合です。有界な閉集合は、コンパクト集合として一般化されます。そこで

\[C_c ^\infty(\Omega) :=\{\phi \in C^\infty(\Omega) \mid \phi の台はコンパクト\}\]

と定義します。何回でも微分できて、かつ台がコンパクトであるような関数の集合です。この条件を満たす関数を、テスト関数（test function）と呼びます。\(C_c ^\infty(\Omega)\)のほかに、\(C_0 ^\infty(\Omega), \mathcal{D}(\Omega)\)という記号を用いることもあります。

ちなみに慣習的な話ですが、テスト関数は他の関数\(f,g,u,v\)などを区別するため、ファイ\(\phi,\varphi\)を用いることが多いです。そうしなければならないというものではありませんが、計算の中で\(\phi\)が出てきたら、「ああこれはテスト関数として計算できる」と考えやすくなります。

さきほどの例で挙げた関数は、台\([-1,1]\)がコンパクトであるものの、\(x=-1,1\)においては微分可能ではありません。したがって、テスト関数ではありません。テスト関数の例を挙げましょう。

\[ \phi(x)= \left\{ \begin{array}{lr} e^{-\frac{1}{1-x^2}} && (|x|<1) \\ 0 && (|x| \geq 1) \end{array} \right. \]

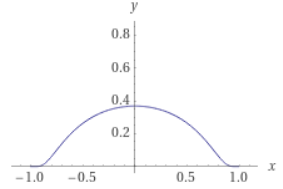
\(|x|<1\)においては、指数関数によって0でない値を取るので、\(\mathrm{supp }\, \phi = [-1,1]\)となり、台はコンパクトです。

\(|x|<1\)においては、指数関数と多項式関数の分数関数の合成なので、何回でも微分可能です。\(|x|>1\)においては、定数関数なので何回でも微分可能です。

問題は\(x=-1,1\)における微分可能性です。内側\(|x|<1\)においては、\(e^{-\frac{1}{x}}\)の微分可能性と同様の議論で\(\phi^{(n)}(x)=\frac{1}{(1-x^2)^{2n}}p_n(x) e^{-\frac{1}{1-x^2}}\)（\(p_n\)は多項式）となります。したがって、指数関数の減衰の強さによって、\(\lim_{x \nearrow 1} \phi^{(n)}(x)=0\)です。また、外側においては常に値が0なので、\(\lim_{x \searrow 1} \phi^{(n)}(x)=0\)です。よって片側微分係数が一致するので、何回でも微分可能と言えました。

よって、\(\phi \)はテスト関数です（\(\phi \in C^\infty _c (\mathbb{R})\)）。

この関数はテスト関数の代表的な例で、適当な定数をかけることで次のような性質を持つようにできます。

\(\phi (x) \geq 0\)
\(|x| \geq 1\)ならば、\(\phi (x) =0\)
\(\int _{\mathbb{R}} \phi(x)=1\)

さらに、

\[ \phi(x)= \left\{ \begin{array}{lr} e^{-\frac{1}{1-\|x\|^2}} && (\|x\|<1) \\ 0 && (\|x\| \geq 1) \end{array} \right. \]

絶対値の部分をノルムに置き換えることで、多次元でもテスト関数になります \(\phi \in C_c^\infty(\mathbb{R}^N)\)。関数の台は円や球です。

さらに、この関数をうまく定数倍や変数変換することで、畳み込みによって相手の関数をなめらかに近似する、軟化作用素（molifier 軟化子）を構成できます。

以上、テスト関数、関数の台とは何か、簡単な例を通じて紹介してきました。

テスト関数は、何回も微分できて、有限な部分以外での値が0となるような都合の良い関数です。

弱微分の理論においては、テスト関数は「なめらかで都合の良い関数」として記号\(\phi\)のまま扱うことが多く、その具体的な形は知らなくても不都合は多くありません。テスト関数の微分は\(\phi ^{\prime}\)で、2階微分は\(\phi ^{\prime \prime}\)、一般階の微分は\(D^{\alpha} \phi\)と表せるわけです。

しかし、「そんな都合の良い関数は存在するのか」「どんな計算をしているのかイメージでつかみたい」と思うならば、今回紹介したような具体例を知っておくのは大事だと思います。

木村すらいむ（@kimu3_slime）でした。ではでは。