中心モーメントとは：歪度、尖度、n次モーメントとの関係

どうも、木村（@kimu3_slime）です。

今回は、中心モーメントとは何か、n次モーメントとの関係を紹介します。

中心モーメントとは
n次モーメントとの関係
こちらもおすすめ

中心モーメントとは

確率変数\(X\)の実数\(a\)を中心とする\(n\)次のモーメントとは、期待値\(E((X-a)^n)\)のことです。

原点\(a=0\)を中心とする\(n\)次のモーメント\(\mu_n^{\prime} =E(X^n)\)を、単に\(n\)次のモーメントと呼びます。

例えば、平均（期待値）\(E(X)\)は、1次のモーメントです。

平均\(a=E(X)\)を中心とする\(n\)次のモーメント\(\mu_n =E((X-E(X))^n)\)を、単に中心モーメント（central moment）と呼びます。

例えば、分散\(V(X)=E((X-E(X))^2)\)は2次の中心モーメントです。

中心モーメントを標準偏差\(\mathrm{Std}(X)=\sqrt{V(X)}\)で正規化した\(\frac{E((X-E(X))^n)}{(\mathrm{Std}(X))^n}\)を、\(n\)次の標準化モーメント（standardized moment）と呼びます。

3次の標準化モーメント\(\frac{E((X-E(X))^3)}{(\mathrm{Std}(X))^3}\)は、歪度（skewness）と呼ばれます。

4次の標準化モーメント\(\frac{E((X-E(X))^4)}{(\mathrm{Std}(X))^4}\)は、尖度（kurtosis）と呼ばれます。

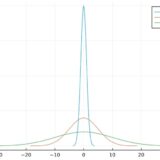
正規分布の尖度が0となるように調整された、超過尖度（excess kurtosis）\(\frac{E((X-E(X))^4)}{(\mathrm{Std}(X))^4}-3\)はよく用いられます。

歪度や尖度は、平均や分散と同様、分布の特徴を調べるために使われる統計量です。

n次モーメントとの関係

中心モーメントは定義としてはわかりやすいですが、計算が少し面倒です。そこで、原点を中心とするモーメントに書き換えると計算が楽になります。

例えば、2次の中心モーメントである分散は

\[V(X) = E(X^2)- (E(X))^2\]

と2次、1次の原点中心のモーメントによって表せます。この関係を一般化してみましょう。

中心モーメントの中身を二項展開し、期待値の定数倍、和の性質を用いれば

\[\begin{aligned} &\quad E((X-E(X))^n)\\&= E(\sum_{k=0}^n C(n,k) X^k (-E(X))^{n-k})\\ &= \sum_{k=0}^n C(n,k)(-1)^{n-k} E(X^k)(E(X))^{n-k}\end{aligned}\]

という関係が成り立ちます。

\(n=2\)のときが、分散の関係式です。

\(n=3\)のときは、

\[\begin{aligned} &\quad E((X-E(X))^3)\\ &= \sum_{k=0}^3 C(3,k)(-1)^{3-k} E(X^k)(E(X))^{3-k} \\&= E(X^3)-3E(X^2)E(X) +3E(X)(E(X))^2 -(E(X))^3\\ &= E(X^3)-3E(X^2)E(X)+2(E(X))^3\end{aligned}\]

\(n=4\)のときは、

\[\begin{aligned} &\quad E((X-E(X))^4)\\ &= \sum_{k=0}^4 C(4,k)(-1)^{4-k} E(X^k)(E(X))^{4-k} \\&= E(X^4)-4E(X^3)E(X)\\&\quad+6E(X^2)(E(X))^2-4E(X)(E(X))^3+(E(X))^5\\&=E(X^4)-4E(X^3)E(X)\\&\quad+6E(X^2)(E(X))^2-3(E(X))^4\end{aligned}\]

となります。

原点中心のモーメントはモーメント生成関数から計算できることが多いので、これらの関係式を使えば歪度や尖度が計算しやすいです。

以上、中心モーメントとは何か、歪度、尖度、n次モーメントとの関係を紹介してきました。

具体的な確率分布の歪度、尖度の計算は、別記事で紹介予定です。

木村すらいむ（@kimu3_slime）でした。ではでは。