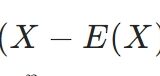どうも、木村(@kimu3_slime)です。
今回は、正規分布の歪度・尖度の求め方について、キュムラント生成関数を使った方法を紹介します。
キュムラントと歪度・尖度
\(X\)を確率変数として、\(\frac{E((X-E(X))^3)}{(\mathrm{Std}(X))^3}\)が歪度、\(\frac{E((X-E(X))^4)}{(\mathrm{Std}(X))^4}-3\)が(超過)尖度です。
これらを計算するために、中心モーメントの展開式
\[\begin{aligned} &\quad E((X-E(X))^3) \\&= E(X^3)-3E(X^2)E(X)+2(E(X))^3\end{aligned}\]
\[\begin{aligned} &\quad E((X-E(X))^4)\\&=E(X^4)-4E(X^3)E(X)\\&\quad+6E(X^2)(E(X))^2-3(E(X))^4\end{aligned}\]
が使えます。
\(X\)を正規分布\(\mathrm{Normal}(\mu,\sigma)\)に従う確率変数としましょう。そのモーメント生成関数は
\[M_{X} (t) =\exp(\mu t+ \frac{1}{2}\sigma^2 t^2 )\]
です。その微分を計算すれば、原理的には高次のモーメントが求められるのですが、式が複雑になります。
そこでモーメント生成関数の対数関数
\[K_X(t):=\log (M_X(t)) \]
を考えましょう。これを\(X\)のキュムラント生成関数(cumulant generating function)と呼びます。
例えば正規分布に従う確率変数の場合は、
\[K_{X} (t) =\mu t+ \frac{1}{2}\sigma^2 t^2 \]
です。これなら微分が計算しやすいですね。
キュムラント生成関数をテイラー展開
\[K_X(t) = \sum_{k=1}^\infty \frac{t^k}{k!}\frac{d^{n}}{dt^n} K_X(0)\]
したときの係数\(\kappa_k =\frac{d^{k}}{dt^k} K_X(0)\)を、\(k\)次のキュムラントと呼びます。
0次のモーメントは\(M_X(0)=E(X^0)=1\)なので、0次のキュムラントは\(K_X(0)=\log(M_X(0))=0\)となることに注意しましょう。
キュムラントとモーメントの関係は、次のようになっています。対数関数のテイラー展開
\[\log(1+x) = x- \frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+o(x^4)\]
に気をつけて(\(o\)はオーダー記号)、
\[\begin{aligned}&\quad \log(M_X(t)) \\&= \log(\sum_{\ell=0}^\infty \frac{t^\ell}{\ell!} E(X^\ell))\\&=\log(1+\sum_{\ell=1}^\infty \frac{t^\ell}{\ell!} E(X^\ell)) \\&= \sum_{\ell=1}^\infty \frac{t^\ell}{\ell!} E(X^\ell) -\frac{1}{2}(\sum_{\ell=1}^\infty \frac{t^\ell}{\ell!} E(X^\ell))^2\\&+\frac{1}{3}(\sum_{\ell=1}^\infty \frac{t^\ell}{\ell!} E(X^\ell))^3-\frac{1}{4}(\sum_{\ell=1}^\infty \frac{t^\ell}{\ell!} E(X^\ell) )^4+o(t^4)\\&=\sum_{\ell=1}^\infty \frac{t^\ell}{\ell!} E(X^\ell) \\&\quad-\frac{1}{2}(t^2(E(X))^2+t^3E(X)E(X^2) \\&\quad +\frac{1}{4}t^4(E(X^2))^2 +\frac{2}{3!} t^4E(X)E(X^3))\\&\quad+\frac{1}{3}(t^3 (E(X))^3+\frac{3}{2}t^4 (E(X))^2 E(X^2)) \\&\quad -\frac{1}{4}t^4(E(X))^4+o(t^4)\\&=tE(X)+\frac{t^2}{2!}(E(X^2)-(E(X))^2)\\&\quad +\frac{t^3}{3!}(E(X^3) E(X^3)-3E(X^2)E(X)+2(E(X))^3)\\&\quad +\frac{t^4}{4!}(E(X^4)-4E(X^3)E(X)-3(E(X^2))^2\\&\quad+12E(X^2)(E(X))^2-6(E(X))^4)+o(t^4)\end{aligned}\]
と展開できます。
\(t\)について展開の係数を比較し、中心モーメントの展開式を使って整理すると、
\[\kappa_1 =E(X)\]
\[\kappa_2 =E(X^2)-(E(X))^2=V(X)\]
\[\begin{aligned} \kappa_3 &= E(X^3) E(X^3)-3E(X^2)E(X)+2(E(X))^3\\&=E((X-E(X))^3) \end{aligned}\]
\[\begin{aligned} \kappa_4 &= E(X^4)-4E(X^3)E(X)\\&\quad+6E(X^2)(E(X))^2-3(E(X))^4\\ &\quad -3(E(X^2)-(E(X))^2)^2 \\&= E((X-E(X))^4)-3(V(X))^2\end{aligned}\]
となります。
よって、歪度と尖度はキュムラントを使って、
\[\frac{E((X-E(X))^3)}{(\mathrm{Std}(X))^3} = \frac{\kappa_3}{(\mathrm{Std}(X))^3}\]
\[\frac{E((X-E(X))^4)}{(\mathrm{Std}(X))^4}-3 = \frac{\kappa_4}{(\mathrm{Std}(X))^4}\]
と表せます。かなり計算しやすくなりました。超過尖度の定義で\(-3\)を加えるのも自然に見えますね。
正規分布の歪度・尖度
キュムラントを使って、正規分布の歪度・尖度を計算してみましょう。
\[K_{X} (t) =\mu t+ \frac{1}{2}\sigma^2 t^2 \]
だったので、その微分は
\[\frac{d}{dt}K_X(t) =\mu +\sigma^2 t\]
\[\frac{d^2}{dt^2}K_X(t) =\sigma^2 \]
\[\frac{d^k}{dt^k}K_X(t) =0 \quad (k \geq 3)\]
となります。したがって、
\[\kappa_1 = \mu , \kappa_2 =\sigma^2\]
\[\kappa_3 = \kappa_4 =0\]
です。よって、歪度と尖度は
\[ \frac{\kappa_3}{(\mathrm{Std}(X))^3} =0\]
\[\frac{\kappa_4}{(\mathrm{Std}(X))^4} =0\]
共に0になることがわかりました。
分散というパラメータをいかに変えても、歪度と尖度は0になっています。
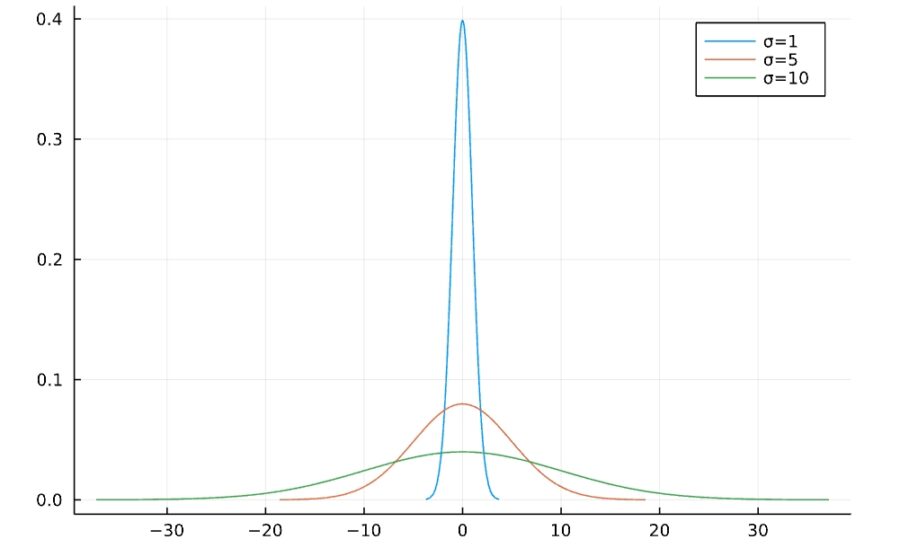
尖度という用語は、必ずしも見た目の尖り具合を意味していないことに注意しましょう。上の図では\(\sigma =1\)が相対的に尖っているように見えますが、どれもともに尖度0です。確率分布が平均値付近以外=裾にどれだけ広がっているか、裾の相対的な重さを表す指標と捉えたほうが良いでしょう。
以上、正規分布の歪度・尖度の求め方について、キュムラント生成関数を使った方法を紹介してきました。
歪度・尖度の概念は、他の分布と比較するとよりわかりやすいでしょう。別記事にて紹介予定です。
木村すらいむ(@kimu3_slime)でした。ではでは。
Probability and Statistics: Pearson New International Edition
Pearson Education Limited (2013-07-30T00:00:01Z)
¥10,792 (中古品)
培風館 (1978-01-01T00:00:01Z)
¥5,280
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥5,862 (中古品)
こちらもおすすめ
有名な極限の公式f(x)/xの覚え方:接線近似とテイラー展開