どうも、木村(@kimu3_slime)です。
今回は、Julia(SymPy)で指数行列、線形常微分方程式を解く方法を紹介します。
前提知識:線形常微分方程式を行列で解く:行列の指数関数を解説
準備
SymPy、Plots、PlotlyJSを使うので、持っていなければインストールしておきましょう。
1 2 3 4 | using Pkg Pkg.add("SymPy") Pkg.add("Plots") Pkg.add("PlotlyJS") |
準備として、以下のコードを実行しておきます。
1 2 3 | using SymPy using Plots plotlyjs() |
指数行列を計算する方法
最初に、今回使う変数記号を用意しておきます。
1 | @vars a b θ x y z t |
「exp(行列)」で指数行列(行列の指数関数)が計算できます。
1 2 | A = Sym[a 0; 0 b] exp(A) |
\[ \begin{aligned}\left[ \begin{array}{rr}e^{a}&0\\0&e^{b}\end{array}\right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{rr}e^{a}&0\\0&e^{b}\end{array}\right]\end{aligned} \]
対角化不可能な例であっても、ジョルダン標準形を通してきちんと計算されます。
1 2 | B = Sym[1 1; 0 1] exp(B) |
\[ \begin{aligned}\left[ \begin{array}{rr}1&1\\0&1\end{array}\right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{rr}e&e\\0&e\end{array}\right]\end{aligned} \]
対角成分が0の交代行列の指数行列を求めてみましょう。
1 2 | C = [0 -θ; θ 0] exp(C) |
\[ \begin{aligned}\left[ \begin{array}{rr}0&- θ\\θ&0\end{array}\right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{rr}\frac{e^{i θ}}{2} + \frac{e^{- i θ}}{2}&\frac{i e^{i θ}}{2} – \frac{i e^{- i θ}}{2}\\- \frac{i e^{i θ}}{2} + \frac{i e^{- i θ}}{2}&\frac{e^{i θ}}{2} + \frac{e^{- i θ}}{2}\end{array}\right]\end{aligned} \]
複素指数関数が出てきていますが、「sympy.simplify(行列)」でその成分を単純化できます。
1 | sympy.simplify(exp(C)) |
これは回転行列ですね。
線形常微分方程式を解く方法
指数行列の応用には、線形常微分方程式の解法があります。
\[ \begin{aligned}\frac{du}{dt} = Au\end{aligned} \]
\[ \begin{aligned}u(0) =u_0\end{aligned} \]
という初期値問題の解は、\(u(t) = e^{tA}u_0\)と表わせます。
次の線形常微分方程式を、指数行列を求めることによって解いてみましょう。
\[ \begin{aligned}\begin{pmatrix} \frac{dx}{dt}\\ \frac{dy}{dt} \end{pmatrix}=\begin{pmatrix} -1&1\\-1&-1 \end{pmatrix} \begin{pmatrix} x\\y \end{pmatrix}\end{aligned} \]
1 2 | D = Sym[-1 1; -1 -1] sympy.simplify(exp(t*D)) |
\[ \begin{aligned}\left[ \begin{array}{rr}-1&1\\-1&-1\end{array}\right]\end{aligned} \]
\[ \begin{aligned}\left[\begin{smallmatrix}e^{- t} \cos{\left(t \right)} & e^{- t} \sin{\left(t \right)}\\- e^{- t} \sin{\left(t \right)} & e^{- t} \cos{\left(t \right)}\end{smallmatrix}\right]\end{aligned} \]
初期値を\(u_0=(x,y)\)とするとき、その解は
1 | convert(Matrix{Sym}, sympy.simplify(exp(t*D)) )*Sym[x,y] |
\[ \begin{aligned}\left[ \begin{array}{r}x e^{- t} \cos{\left(t \right)} + y e^{- t} \sin{\left(t \right)}\\- x e^{- t} \sin{\left(t \right)} + y e^{- t} \cos{\left(t \right)}\end{array} \right]\end{aligned} \]
となります。simplifyする過程で型が行列の計算に適さなくなってしまうので、「convert」によってSym型に戻して計算しています。
初期値を具体的な値にするには、「subs(変数,数値)」を用いれば良いです。例えば、\((1,1)\)を初期値とする解は
1 | (convert(Matrix{Sym}, sympy.simplify(exp(t*D)) )*Sym[x,y]).subs(([x,1],[y,1])) |
\[ \begin{aligned}\left[ \begin{array}{r}e^{- t} \sin{\left(t \right)} + e^{- t} \cos{\left(t \right)}\\- e^{- t} \sin{\left(t \right)} + e^{- t} \cos{\left(t \right)}\end{array}\right]\end{aligned} \]
です。
これを曲線としてプロットしてみると、
1 2 3 4 | plot((convert(Matrix{Sym}, sympy.simplify(exp(t*D)) )*Sym[x,y]).subs(([x,1],[y,1]))[1], (convert(Matrix{Sym}, sympy.simplify(exp(t*D)) )*Sym[x,y]).subs(([x,1],[y,1]))[2], 0, 5, xlabel = "x", ylabel = "y") |
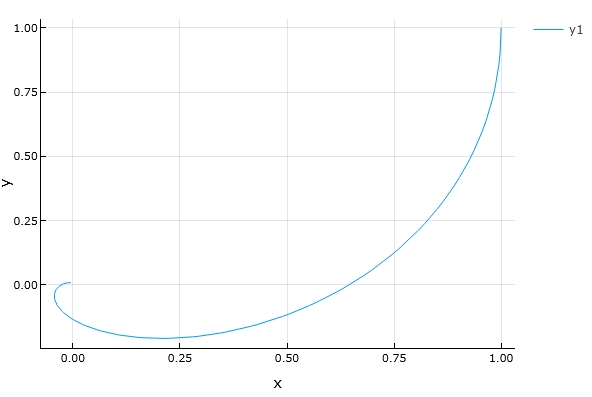
\(u_0=(1,1)\)から出発した解が、原点に引き込まれていることがわかります。
参考:方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門
3変数の線形常微分方程式についても、同じように解いてグラフを描いてみましょう。
1 2 3 4 | E = Sym[1 3 -2; -1 3 0; -1 0 3] exp(t*E) exp(t*E)*Sym[x,y,z] (exp(t*E)*Sym[x,y,z]).subs(([x,2],[y,1],[z,3])) |
\[ \begin{aligned}\left[ \begin{array}{rrr}1&3&-2\\-1&3&0\\-1&0&3\end{array}\right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{rrr}- t e^{2 t} + e^{2 t}&3 t e^{2 t}&- 2 t e^{2 t}\\- t e^{2 t}&3 t e^{2 t} – 2 e^{3 t} + 3 e^{2 t}&- 2 t e^{2 t} + 2 e^{3 t} – 2 e^{2 t}\\- t e^{2 t}&3 t e^{2 t} – 3 e^{3 t} + 3 e^{2 t}&- 2 t e^{2 t} + 3 e^{3 t} – 2 e^{2 t}\end{array}\right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{r}3 t y e^{2 t} – 2 t z e^{2 t} + x \left(- t e^{2 t} + e^{2 t}\right)\\- t x e^{2 t} + y \left(3 t e^{2 t} – 2 e^{3 t} + 3 e^{2 t}\right) + z \left(- 2 t e^{2 t} + 2 e^{3 t} – 2 e^{2 t}\right)\\- t x e^{2 t} + y \left(3 t e^{2 t} – 3 e^{3 t} + 3 e^{2 t}\right) + z \left(- 2 t e^{2 t} + 3 e^{3 t} – 2 e^{2 t}\right)\end{array} \right]\end{aligned} \]
\[ \begin{aligned}\left[ \begin{array}{r}- 5 t e^{2 t} + 2 e^{2 t}\\- 5 t e^{2 t} + 4 e^{3 t} – 3 e^{2 t}\\- 5 t e^{2 t} + 6 e^{3 t} – 3 e^{2 t}\end{array}\right]\end{aligned} \]
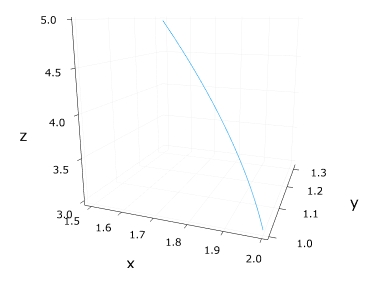
\(u_0=(2,1,3)\)を出発した解は、原点から離れていくことが読み取れます。\(e^{2t},e^{3t}\)が成分に含まれているので、その項の大きさは\(t\to \infty\)で大きくなっていくわけです。
固有値を計算してみると、
1 | E.eigenvals() |
1 2 3 | Dict{Any, Any} with 2 entries: 3 => 1 2 => 2 |
実部が正の固有値が存在するので、原点は不安定です。
参考:線形微分方程式の解の安定性は「固有値」を調べればわかる
以上、Julia(SymPy)で指数行列、線形常微分方程式を解く方法を紹介してきました。
ジョルダン標準形を表に出さずとも指数行列を計算してくれますし、記号を含んでいてもきれいに計算できるので、とても便利です。
木村すらいむ(@kimu3_slime)でした。ではでは。
コロナ社 (2020-03-26T00:00:01Z)
¥7,353 (コレクター商品)
こちらもおすすめ
オイラーの公式、極形式、ド・モアブルの定理とは:複素指数関数、三角関数の性質
方程式を解かずに、解の軌跡・安定性を調べてみよう 力学系理論入門
Julia(SymPy)で固有値、固有ベクトル、対角化、ジョルダン標準形を求める方法