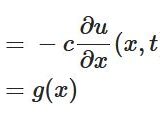どうも、木村(@kimu3_slime)です。
今回は、2階偏微分方程式の分類として、楕円型、放物型、双曲型とは何かを紹介します。
予備知識:偏微分方程式とは:2階線形の重要な例(ラプラス、熱、波動)
一般的な2階偏微分方程式として
\[ \begin{aligned}a\frac{\partial ^2 u}{\partial x^2}+b\frac{\partial ^2 u}{\partial x \partial y}+c\frac{\partial ^2 u}{\partial y^2}=F(x,y,u,\frac{\partial u}{\partial x},\frac{\partial u}{\partial y})\end{aligned} \]
を考えましょう。これを準線形(quasilinear)偏微分方程式と呼びます。2回偏導関数に関しては線形で、それ以下の項は場合によるケースです。
この方程式の性質は、2回微分の係数の判別式\(b^2-4ac\)の符号によって、楕円型、放物型、双曲型の3つに分類されます。
楕円型方程式(elliptic equation)
\(b^2-4ac <0\)のとき、方程式は楕円型(だえんがた)と呼ばれます。
例えば、ラプラス方程式
\[ \begin{aligned}\frac{\partial ^2 u}{\partial x^2}+\frac{\partial ^2 u}{\partial y^2}=0\end{aligned} \]
やポアソン方程式
\[ \begin{aligned}\frac{\partial ^2 u}{\partial x^2}+\frac{\partial ^2 u}{\partial y^2}=f(x,y)\end{aligned} \]
は、\(a=c=1,b=0\)に対応する楕円型方程式です。
右辺に\(u\)に関する項を含む方程式
\[ \begin{aligned}-\Delta u=f(u)\end{aligned} \]
は、非線形ポアソン方程式と呼ばれる楕円型方程式です。
\[ \begin{aligned}-\Delta u=\lambda u\end{aligned} \]
という形のときは、(ラプラシアンの)固有値問題、ヘルムホルツの方程式と呼ばれています。
放物型方程式(parabolic equation)
\(b^2 -4ac=0\)のとき、方程式は放物型(ほうぶつがた)と呼ばれます。
\[ \begin{aligned}\frac{\partial u}{\partial t}-\frac{\partial ^2 u}{\partial x^2}=0\end{aligned} \]
は、\(a=-1,b=c=0\)で、放物型方程式です。
右辺に\(u\)に関する項が加わった放物型方程式
\[ \begin{aligned}\frac{\partial u}{\partial t}-\frac{\partial ^2 u}{\partial x^2}=f(u)\end{aligned} \]
は、(単独)反応拡散方程式(reaction-diffusion equation)と呼ばれています。
参考:生き物の模様は数式で決まる? チューリング・パターンとは
双曲型方程式(hyperbolic equation)
\(b^2 -4ac>0\)のとき、方程式は双曲型(そうきょくがた)と呼ばれます。
\[ \begin{aligned}\frac{\partial ^2 u}{\partial t^2}-c^2\frac{\partial ^2 u}{\partial x^2}=0\end{aligned} \]
は、\(y=ct\)と変数変換したもので、\(a=1,b=0,c=-1\)に対応する双曲型方程式です。熱方程式と違って、時間の2回微分が出てくるので、そこがカウントされています。
右辺に\(u\)に関する項を加えた双曲型方程式
\[ \begin{aligned}\frac{\partial ^2 u}{\partial t^2}-c^2\frac{\partial ^2 u}{\partial x^2}=f(u)\end{aligned} \]
は、非線形波動方程式と呼ばれています。
今回の分類方法とは少し違いますが、1階の偏微分方程式である移流方程式(輸送方程式)
\[ \begin{aligned}\frac{\partial u}{\partial t}-c\frac{\partial u}{\partial x}=0\end{aligned} \]
も、双曲型方程式に分類されます。実際、波動方程式を解く中で、移流方程式が得られます。波のように量が保存され、ある方向に進行するのは同様です。
方程式を楕円型、放物型、双曲型と呼びましたが、これらは解の形が楕円型であったりするからそう名付けているわけではありません。
2次曲線
\[ \begin{aligned}ax^2+bxy+cy^2=F(x,y)\end{aligned} \]
はその係数によって、
- \(b^2-4ac<0\)ならば楕円
- \(b^2-4ac=0\)ならば放物線
- \(b^2-4ac>0\)ならば双曲線
と分類されます(直線に退化するときもありますが)。これらになぞらえて、偏微分方程式を呼び分けているわけですね。
実際、楕円型は楕円型、放物型は放物型、双曲型は双曲型に共通する性質や分析手法があります。
以上、2階偏微分方程式の分類として、楕円型、放物型、双曲型について紹介してきました。
それぞれラプラス方程式、熱方程式、波動方程式を一般化したものです。楕円型方程式と言われても怖がらずに、ラプラス方程式を一般化したようなものだな、と思えるようになってみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
Pearson (2016-03-02T00:00:00.000Z)
¥4,910
Advanced Engineering Mathematics
John Wiley & Sons Inc (2011-05-03T00:00:01Z)
¥6,333 (中古品)
朝倉書店 (2002-01-01T00:00:01Z)
¥2,215 (中古品)
Partial Differential Equations (Graduate Studies in Mathematics)
Amer Mathematical Society (2010-04-02T00:00:01Z)
¥9,531 (中古品)
こちらもおすすめ
熱方程式の解き方:変数分離法、フーリエ級数展開(1次元、有界領域)