偏微分方程式とは：2階線形の重要な例（ラプラス、熱、波動）

どうも、木村（@kimu3_slime）です。

今回は、偏微分方程式とは何か、2階線形方程式の重要な例（ラプラス、熱、波動）を紹介します。

偏微分方程式とは
偏微分方程式の線形性
こちらもおすすめ

偏微分方程式とは

偏微分方程式（partial differential equation, PDE）とは、

\[ \begin{aligned}\frac{\partial u}{\partial t} = \frac{\partial ^2 u}{\partial x^2} +\frac{\partial ^2 u}{\partial y^2}\end{aligned} \]

のように、未知関数\(u(x,y,t)\)の偏微分を含む方程式です。

常微分方程式は、偏微分方程式の特殊なケースと言えます。例えばニュートンの運動方程式

\[ \begin{aligned}m\frac{d^2 x} {dt ^2} =F(x,\frac{dx}{dt},t)\end{aligned} \]

は、未知関数\(x(t)\)の1つの変数\(t\)に関する微分しか含まない方程式です。一般に、未知関数の複数の変数に関する偏微分を含む方程式が、偏微分というわけです。

偏微分方程式の中でも、数学的に扱いやすく、かつ応用が幅広いのが次の3つの方程式です。

ラプラス方程式（Laplace equation）

\[ \begin{aligned}\frac{\partial ^2 u}{\partial x^2} +\frac{\partial ^2 u}{\partial y^2}=0\end{aligned} \]

これは時間によって変化しない定常状態の方程式として見ることができます。以降で紹介する熱方程式、波動方程式において、時間微分が0\(\frac{\partial u}{\partial t}=0\)としたものがラプラス方程式です。

この方程式に表れる2回微分の和

\[ \begin{aligned}\Delta u := \frac{\partial ^2 u}{\partial x^2} +\frac{\partial ^2 u}{\partial y^2}\end{aligned} \]

はラプラシアン\(\Delta u\)と呼ばれています。つまり、ラプラス方程式は\(\Delta u=0\)と表せます。以降でもこの記法を使いましょう。

重力のポテンシャル（位置エネルギー）、クーロン力（静電引力）のポテンシャルは、ラプラス方程式を満たすことが知られています。ラプラス方程式の解は調和関数（Harmonic function）と呼ばれ、特にその性質を調べる分野はポテンシャル論と呼ばれるています。

複素微分可能な関数（正則関数）の実部、虚部もラプラス方程式を満たすことが知られています。

参考：複素微分、正則関数・解析関数とは：具体例をもとに

熱方程式（heat equation）

\[ \begin{aligned}\frac{\partial u}{\partial t} = \Delta u\end{aligned} \]

この方程式は、熱伝導に関するフーリエの法則から導かれます。

参考：なぜ偏微分を学ぶ？フーリエの熱伝導方程式を例に、なぜ重積分を学ぶ？熱伝導方程式の導出を例に

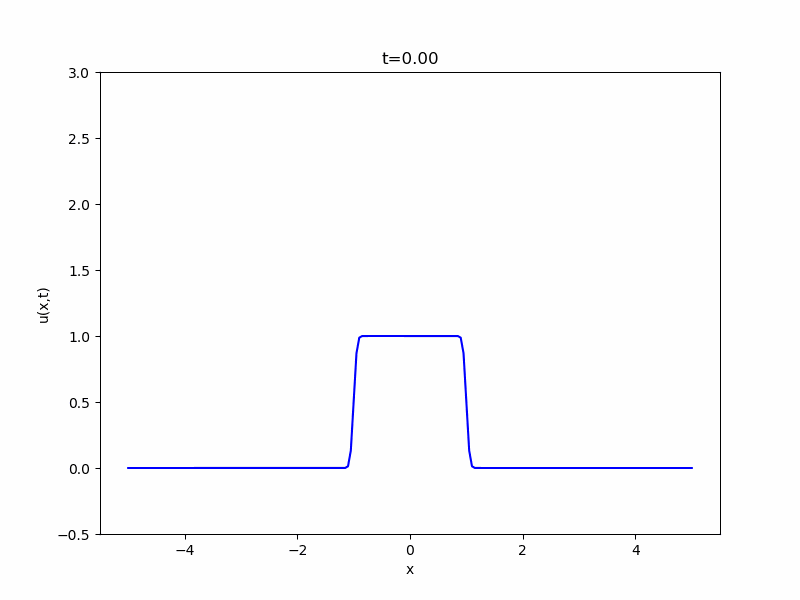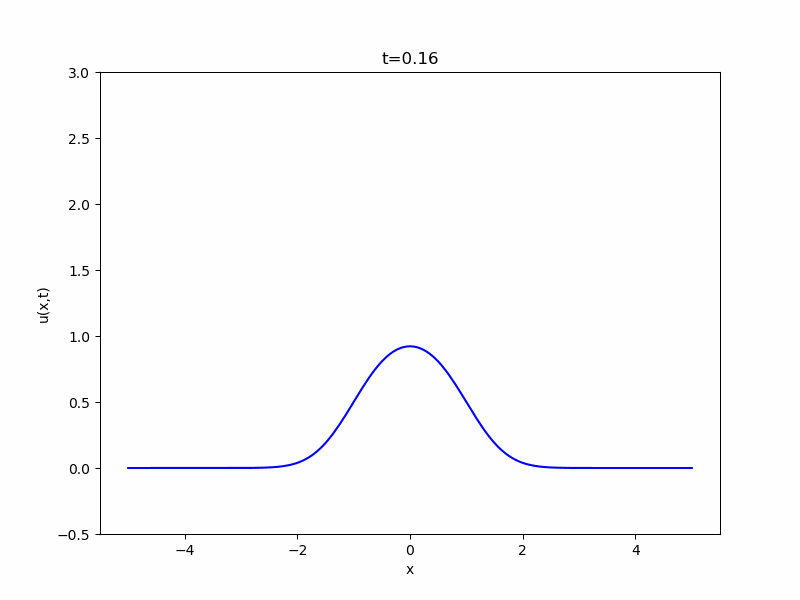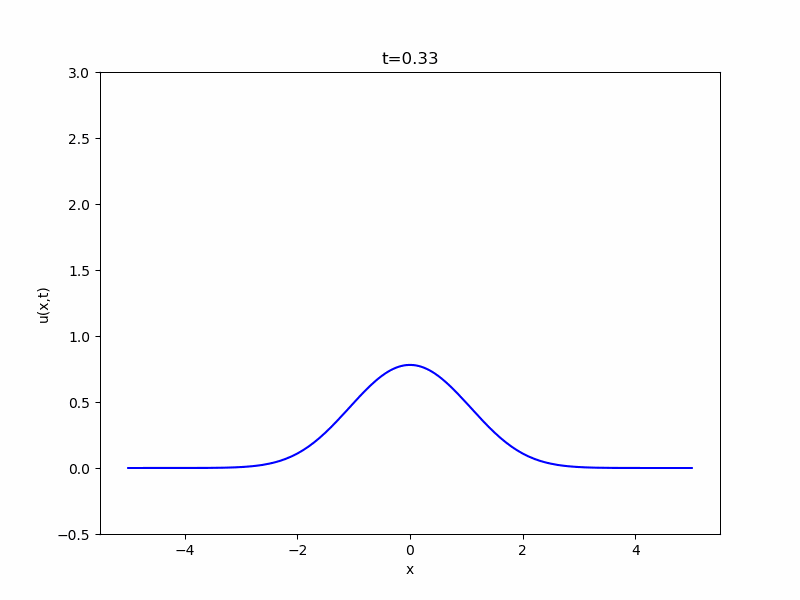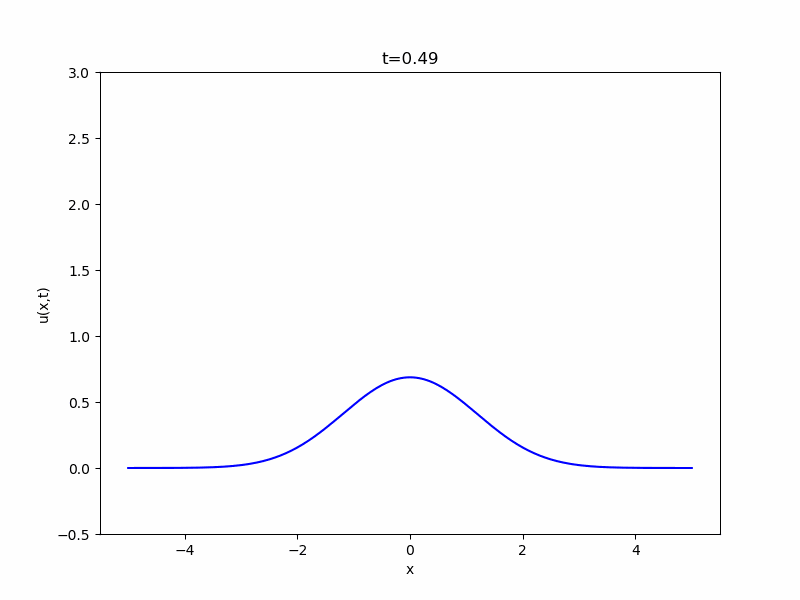
フーリエ級数、フーリエ展開の理論は現在幅広く応用されていますが、もともとはフーリエがこの方程式を解こうとする中で発見した手法です。

参考：熱方程式の解き方：変数分離法、フーリエ級数展開（1次元、有界領域）、線形代数の応用：関数の「空間・基底・内積」を使ったフーリエ級数展開、三角関数の直交性とは：フーリエ級数展開と関数空間の内積

熱伝導現象だけでなく、細かい物質の拡散現象も同じ方程式によって説明できます。

参考：花粉の広がりを数式で予測する、拡散方程式とは

波動方程式（Wave equation）

\[ \begin{aligned}\frac{\partial u}{\partial t} = \Delta u\end{aligned} \]

時間について2階微分を含むのが、波動方程式です。

波動方程式は、弦の振動、波動現象の説明に使われ、流体力学の基礎となるシンプルな方程式と言えます。

参考：波の重ね合わせの原理はなぜ成り立つ？波動方程式入門

偏微分方程式の線形性

ラプラス方程式、熱方程式、波動方程式に共通することは何でしょうか。

\[ \begin{aligned}\Delta u=0\end{aligned} \]

\[ \begin{aligned}\frac{\partial u}{\partial t} = \Delta u\end{aligned} \]

まず、含まれる微分の回数の最大回数が2ということです。そのため、2階偏微分方程式（second order PDE）と呼ばれています。

さらに重要なのは、これらが線形方程式（linear PDE）ということです。

線形とは何かというと、\(u,v\)を方程式の解、\(c\)をスカラーとすると、重ね合わせや定数倍\(cu +v\)もまた方程式の解となることです。

どうしてそうなるのでしょうか。まず基礎として、微分には線形性があります。

\[ \begin{aligned}\frac{\partial }{\partial x}(cu+v)=c\frac{\partial u}{\partial x}+ \frac{\partial v}{\partial x}\end{aligned} \]

参考：連続関数、可積分関数の線形空間（関数空間）、微分と積分の線形性とは

したがって、ラプラシアンについても線形性が成り立ちます。

\[ \begin{aligned} \Delta (cu+v) &= \frac{\partial ^2 (cu+v)}{\partial x^2} +\frac{\partial ^2 (cu+v)}{\partial y^2} \\ &= c\frac{\partial^2 u}{\partial x^2}+ \frac{\partial^2 v}{\partial x^2} \\ & +c\frac{\partial^2 u}{\partial y^2}+ \frac{\partial^2 v}{\partial y^2} \\ &= c\Delta u +\Delta v \ \end{aligned} \]

となるわけです。

したがって、\(u,v\)がラプラス方程式の解ならば、\(cu+v\)もラプラス方程式の解です。\(\Delta (cu+v)= c\Delta u +\Delta v = 0\)なので。よって、ラプラス方程式は線形方程式です。

時間微分についても線形性は成り立ちます。したがって、\(u,v\)を熱方程式の解とすると、

\[ \begin{aligned} \frac{\partial (cu+v)}{\partial t} &= c\frac{\partial u}{\partial t}+\frac{\partial v}{\partial t}\\&= c \Delta u +\Delta v \\ &= \Delta (cu+v) \ \end{aligned} \]

となり、\(cu+v\)も熱方程式の解です。したがって、熱方程式は線形方程式です。

全く同様にして、波動方程式も線形方程式であることがわかります。

数学的には解を足し合わせたものがまた解になることを、方程式が線形であると呼びますが、それは重ね合わせの原理とも呼ばれています。逆に言えば、これらの方程式の一般的な解は、バラバラにして調べることもできるわけです。

参考：波の重ね合わせの原理はなぜ成り立つ？波動方程式入門

以上、偏微分方程式とは何か、2階線形の重要な例3つ、ラプラス方程式、熱方程式、波動方程式を紹介してきました。

これらに共通する基本的な性質が、線形性です。どの偏微分方程式を学ぶときでも、まずは線形方程式とはどういうことなのかを知っておくのは基礎中の基礎と言えるでしょう。

木村すらいむ（@kimu3_slime）でした。ではでは。