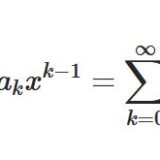ファンデルポール方程式、リミットサイクルとは

どうも、木村（@kimu3_slime）です。

今回は、ファンデルポール方程式、リミットサイクルについて紹介します。

ファンデルポール方程式（van der Pol equation）とは、

\[ \begin{aligned}\frac{d^2x}{dt^2}+\mu (x^2-1)\frac{dx}{dt}+x=0\end{aligned} \]

と表される微分方程式です。ファンデルポール振動子（van der Pol oscillator）、vdP方程式とも。\(\mu \geq 0\)とします。

おもりバネダンパ系、減衰振動の方程式

\[ \begin{aligned}m\frac{d^2 x}{dt^2} +c\frac{dx}{dt}+kx=0 \end{aligned} \]

やRLC回路の方程式

\[ \begin{aligned}\frac{d^2 I}{dt^2} +\frac{R}{L}\frac{dI}{dt} +\frac{1}{LC} I =0\end{aligned} \]

と似ています。

おもりバネダンパ系、RLC回路の方程式では、線形な減衰\(c\frac{dx}{dt}\)を考えていますが、ファンデルポール方程式では非線形な減衰\(\mu (x^2-1)\frac{dx}{dt}\)を考えています。

\(x^2-1\)の部分に注目すれば、\(|x|>1\)ならば通常通りに減衰し、\(|x|<1\)のときは逆の減衰（つまり増幅）が起こります。したがって、解はバランスを保ったまま振動しそうです。

外部から交流を与えずとも交流を生み出すような電気回路は実在し、それは発振回路（electronic oscillator）と呼ばれています。ファンデルポール方程式は、そのような発振現象をモデル化していると言えるでしょう。

\(x_1 =x,x_2 = \frac{dx}{dt}\)と置くことで、方程式を

\[ \begin{aligned} \begin{pmatrix} \frac{dx_1}{dt}\\ \frac{dx_2}{dt} \end{pmatrix} = \begin{pmatrix} x_2\\ -\mu(x_1^2-1)x_2-x_1 \end{pmatrix}\end{aligned} \]

と連立形に変えられます。

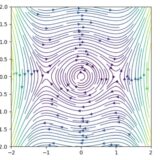
その解の挙動、相図をコンピュータでプロットしてみました。太い線が特定の解曲線を表しています。

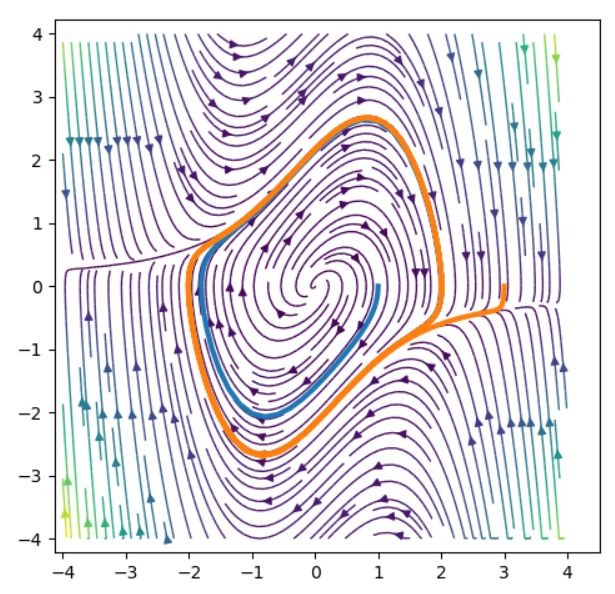
大きさの小さな初期値や、大きな初期値も、やがては閉じた軌道、周期解に近づいていきそうです。

他の解が時間が大きくなっていくときに近づいていくような閉軌道は、リミットサイクル（limit cycle 極限周期軌道）と呼ばれています。

より厳密には、ω極限集合が閉軌道となることと定義されます：極限集合の性質を明らかにするポアンカレ・ベンディクソンの定理

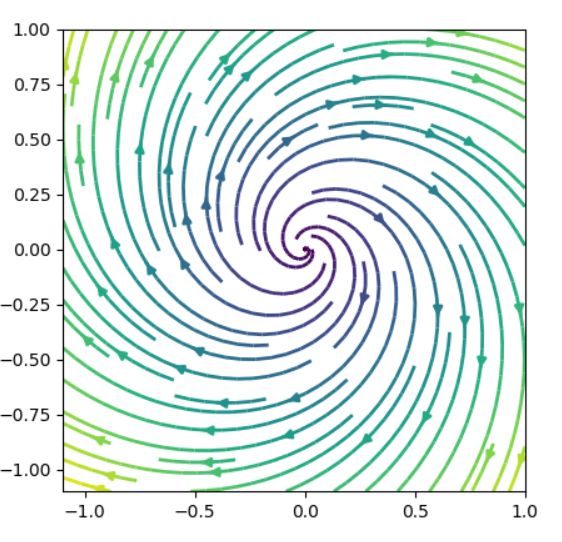
解の挙動について、原点付近では簡単に知ることができます。方程式の平衡解は、原点\((x_1,x_2)=(0,0)\)のみです。

そこでの線形化方程式は

\[ \begin{aligned} \begin{pmatrix} \frac{dx_1}{dt}\\ \frac{dx_2}{dt} \end{pmatrix} = \begin{pmatrix} 0&1\\-1&\mu \end{pmatrix}\begin{pmatrix} x_1\\ x_2 \end{pmatrix}\end{aligned} \]

となり、固有値は\(\lambda =\frac{\mu \pm \sqrt{\mu^2 -4}}{2}\)です。\(\mu >0\)のときは、実部が正の固有値を持つため、不安定です。特に\(\mu < 2\)のときは固有値は複素数で、平衡点は不安定なスパイラルとなることがわかります。

リミットサイクルの存在は、次の定理によって保証できることが知られています。

リエナールの定理（Liénard’s theorem）

\[ \begin{aligned} \begin{pmatrix} \frac{dx_1}{dt}\\ \frac{dx_2}{dt} \end{pmatrix} = \begin{pmatrix} x_2\\ -f(x_1)x_2-g(x_1) \end{pmatrix}\end{aligned} \]

という方程式（リエナールの方程式）を考える。

\(f,g\)が連続微分可能
\(g\)は奇関数
\(x>0\)のとき、\(g(x)>0\)
\(f\)は偶関数
\(F(x):= \int_0^x f(s)ds\)と置く。次の条件を満たす\(a>0\)が存在する。\(F(a)=0\)、\(0<x<a\)ならば\(F(x)<0\)、\(x>a\)ならば\(F(x)>0\)で広義単調増加で、\(\lim_{x\to \infty }F(x)=\infty\)

これらの条件を満たすとき、方程式にはただひとつの漸近安定なリミットサイクルが存在する。

これはファンデルポール方程式を一般化した方程式の性質を調べたと言えます。

\(g\)の仮定は、バネのように復元力が働くこと。\(f\)の仮定は、ある値\(a\)を境に減衰力の方向が変わることです。復元力によって振動が生まれますが、減衰力によって中間の振動状態に落ち着いていきそうですね。

証明についてはPerko「Differential Equations and Dynamical Systems」、Oliver knill “LIENHARD SYSTEMS”を参照してください。

ここでは、ファンデルポール方程式がリエナールの定理の仮定を満たすことを確かめましょう。

\(f(x)= \mu (x^2-1)\)、\(g(x)=x\)、\(F(x) = \mu (\frac{1}{3}x^3-x)\)ですね。\(f,g\)は連続微分可能で、\(g\)は奇関数、\(x>0\)ならば\(g(x)>0\)、\(f\)は偶関数です。\(a=\sqrt{3}\)と置くと、\(F(a)=0\)で、\(x<a\)ならば\(F(x)<0\)、\(x>a\)ならば\(F(x)>0\)です。さらに、\(F\)は\(x>a\)で単調増加で、\(\lim_{x\to \infty} F(x)=\infty\)を満たします。よって、リエナールの定理からリミットサイクルがただひとつ存在すると言えました。

以上、ファンデルポール方程式、リミットサイクルについて紹介してきました。

ファンデルポール方程式のような非線形方程式を解くことは、一般には難しいです（例えば摂動法で近似解を求めることになる）。それでも、線形方程式では見られない現象、自発的に周期解に向かう、リミットサイクルが生まれるのは面白いですね。

木村すらいむ（@kimu3_slime）でした。ではでは。