対称行列のスペクトル分解とは：具体例、証明

どうも、木村（@kimu3_slime）です。

今回は行列のスペクトル分解とは何か、具体例、証明について紹介します。

スペクトル分解の具体例
スペクトル分解とは、証明
こちらもおすすめ

スペクトル分解の具体例

まずは簡単な具体例で、スペクトル分解がどういうものか見てみましょう。

実対称行列

\[ \begin{aligned}\begin{pmatrix} 0 &1\\1 & 0 \end{pmatrix}\end{aligned} \]

を対角化します。途中の計算は省略しますが、固有値は\(1,-1\)で、固有ベクトルを並べた行列は

\[ \begin{aligned}P = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 &1\\1 & -1 \end{pmatrix}\end{aligned} \]

となり、

\[ \begin{aligned}P^{-1}A P =D= \begin{pmatrix} 1 &0\\0 & -1 \end{pmatrix}\end{aligned} \]

と対角化できます。

この行列の対角化の見方を変えたものが、スペクトル分解です。

\(P^{-1}A P =D\)において、対角行列\(D \)を分解して、\(A\)について解いてみましょう。

\[ \begin{aligned} A &=P\begin{pmatrix} 1 &0\\0 & 0 \end{pmatrix}P^{-1}+P\begin{pmatrix} 0 &0\\0 & -1 \end{pmatrix}P^{-1} \end{aligned} \]

右辺の前半を\(P_1\)、後半を\(P_2\)と置く、具体的には

\[ \begin{aligned}P_1 =\frac{1}{2}\begin{pmatrix} 1 &1\\1 & 1 \end{pmatrix}\end{aligned} \]

\[ \begin{aligned}P_2 = \frac{1}{2}\begin{pmatrix} 1 &-1\\-1 & 1 \end{pmatrix}\end{aligned} \]

とすることで、

\[ \begin{aligned} A&=P_1-P_2 \\ &= \lambda_1 P_1 +\lambda_2 P_2\end{aligned} \]

と表せます。ここで\(P_1,P_2\)は射影行列で、\(P_1+P_2=I\)\(P_1P_2=O\)を満たすものとなっています（確かめてみてください）。

このように、与えられた行列を射影行列の固有値倍の和として表すことを、行列\(A\)のスペクトル分解（spectral decomposition）、固有値分解（eigenvalue decomposition）と呼びます。

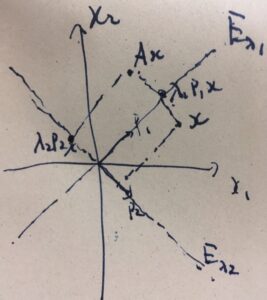
平面上の点\(x\)を\(Ax\)に写すという変換は、（対角化可能な場合）次のように言い換えることができるわけです。

\(A\)の固有値\(\lambda_1,\lambda_2\)に対して、固有空間\(E_{\lambda_1},E_{\lambda_2}\)が定まります。\(x\)の固有空間への射影として、\( P_1 x\)、\( P_2 x\)という射影行列\(P_1,P_2\)が定まります。固有ベクトルからなる基底で見ている上では、行列は対角行列になり、\(E_{\lambda_1}\)方向に\(\lambda_1\)倍、\(E_{\lambda_2}\)方向に\(\lambda_2\)倍されます。したがって、\(\lambda_1 P_1 x+\lambda_2 P_2x\)が\(Ax\)に等しいわけです。

スペクトル分解とは、証明

今までに見てきたことを、一般的に述べてみましょう。

スペクトル分解定理

\(A\)を\(N\)次の実対称行列、\(A\)の異なる固有値を\(\lambda_1,\dots,\lambda_k\)とする。このとき、

\[ \begin{aligned}A= \lambda_1P_1 +\cdots +\lambda_k P_k\end{aligned} \]

\[ \begin{aligned}P_1+\cdots+P_k =I\end{aligned} \]

\[ \begin{aligned} i\neq j \Rightarrow P_i P_j =O\end{aligned} \]

を満たす射影行列\(P_1,\dots,P_k\)がただひとつ存在する。

（行列でなく、線形変換でも同様の主張が成り立つ。）

（複素でも同様の主張が成り立つ。対称行列→正規行列）

（逆も成り立つ。条件を満たす\(P_i,\lambda_i\)があるとき、そこから定まる行列\(A\)は対称行列となる）

証明してみましょう。

簡単のため、対称行列は対角化可能であることを認めて話を進めます。

実対称行列の固有値は実数で、異なる固有値に対応する固有ベクトルは直交します。各固有値に対応する固有空間を\(E_{\lambda_1},\dots,E_{\lambda_k}\)とします。このとき、

\[ \begin{aligned}\mathbb{R}^N= E_{\lambda_1}\oplus \cdots \oplus E_{\lambda_k}\end{aligned} \]

と直交直和に分解できることを示しましょう。

各固有ベクトルが直交しているので、各固有空間が直交していることは良いでしょう。残りは、直和

\[ \begin{aligned}\mathbb{R}^N= E_{\lambda_1}\dot{+} \cdots \dot{+} E_{\lambda_k}\end{aligned} \]

が成り立つかどうかです。

対角化可能であること\(P^{-1}AP =D\)から、\(A\)の固有ベクトルからなる\(\mathbb{R}^N\)の基底が存在することが示せます。標準基底を\(e_1,\dots,e_N\)とするとき、\(Pe_1,\dots,Pe_k\)も基底です。\(P\)は可逆行列であり、全単射なので、基底を基底に対応させます。また、\(P^{-1}APe_i =De_i = \lambda_i e_i\)より、\(APe_i =\lambda_i Pe_i\)なので、\(Pe_i\)は固有ベクトルであるとわかりました。

\(Pe_1,\dots,Pe_k\)が\(\mathbb{R}^N\)の基底なので、任意の\(x \in \mathbb{R}^N\)は\(x= x_1 Pe_1+\cdots+x_k Pe_k\)と一意的に表せます。つまり、直和\(\mathbb{R}^N= E_{\lambda_1}+ \cdots + E_{\lambda_k}\)が成り立つと言えました。

以上によって直和分解

\[ \begin{aligned}\mathbb{R}^N= E_{\lambda_1}\oplus \cdots \oplus E_{\lambda_k}\end{aligned} \]

が成り立つので、各固有空間への直交射影\(P_1,\dots,P_k\)が定まります。

\[ \begin{aligned}x=P_1x+\cdots+P_k x \end{aligned} \]

という分解ができるので、\(A\)を作用させ、固有ベクトルの性質を用いると

\[ \begin{aligned} Ax &= AP_1x +\cdots +AP_k x \\&= \lambda_1 P_1x +\cdots + \lambda_k P_k x\end{aligned} \]

なので、

\[ \begin{aligned}A= \lambda_1P_1 +\cdots +\lambda_k P_k\end{aligned} \]

が得られました。

\[ \begin{aligned}Ix=P_1x+\cdots+P_k x \end{aligned} \]

の見方を変えれば、\(P_1+\cdots+P_k =I\)です。

\(i\neq j\)のとき、\(E_{\lambda_i},E_{\lambda_j}\)は直交しています。したがって、\(E_{\lambda_j} \subset E_{\lambda_i}^{\perp}\)で、\(E_{\lambda_i} \cap E_{\lambda_i}^{\perp}=\{0\}\)です。すべての\(x\)に対し、\(P_i P_j x \in E_{\lambda_i} \cap E_{\lambda_j}\)なので、\(P_iP_j x =0\)。すなわち、\(P_iP_j =O\)が得られました。

最後に、スペクトル分解の一意性を確かめます。仮に

\[ \begin{aligned}A= \lambda_1Q_1 +\cdots +\lambda_k Q_k\end{aligned} \]

\[ \begin{aligned}Q_1+\cdots+Q_k =I\end{aligned} \]

\[ \begin{aligned} i\neq j \Rightarrow Q_i Q_j =O\end{aligned} \]

を満たす射影行列\(Q_1,\dots, Q_k\)があったとしましょう。

\(E_{\lambda_j} =Q_j(\mathbb{R}^N)\)であることが示せます。まず、\(Q_j x\)は\(A\)の\(\lambda_j\)に対応する固有ベクトルです。なぜなら、

\[ \begin{aligned} AQ_j x &= ( \lambda_1Q_1 +\cdots +\lambda_k Q_k)Q_j x \\&= \lambda _j Q_j x \end{aligned} \]

となるので。

\(x\in E_{\lambda_j}\)とすると、\(Ax = \lambda_j x\)です。\(\lambda_j x = \lambda_1 Q_1 x+\cdots+ \lambda_k Q_k x\)となりますが、右辺は\(Q _\ell x \in E_{\lambda_\ell} \)です。直和分解の一意性から\(\lambda_j x = \lambda_j Q_j x\)となり、\(x \in Q_j (\mathbb{R}^N)\)が言えました。

\(x \in Q_j(\mathbb{R}^N)\)とすると、\(x =Q_j y_j\)を満たす\(y_j\)が存在します。ここで\(A\)をかけると

\[ \begin{aligned} Ax &= ( \lambda_1Q_1 +\cdots +\lambda_k Q_k)Q_j y_j \\&= \lambda _j Q_j y_j \\&= \lambda_j x\end{aligned} \]

なので、\(x \in E_{\lambda_j} \)です。

よって、\(P_j(\mathbb{R}^N)=E_{\lambda_j} =Q_j(\mathbb{R}^N)\)が言えました。\(x \not \in P_j (\mathbb{R}^N)\)のときは、直交条件から\(P_jx =Q_j x =0\)です。\(x \in P_j (\mathbb{R}^N)\)のときは、\(P_j x = Q_jx =\lambda_j x\)です。以上により、\(P_j = Q_j\)となり、一意性が示せました。

以上、対称行列のスペクトル分解とは何か、具体例を紹介し、一般的なケースの証明をしました。

今回は有限次元の線形空間における対称行列を扱っていますが、関数解析という分野では、無限次元の線形空間において対称作用素（自己共役作用素）のスペクトル分解を考えます。これは無限次元バージョンの「対角化」と見れます。一般的なケースを知るためにも、まずは有限次元の場合でスペクトル分解がどういうものか知っておくと良いでしょう。

一般的な主張を理解するのは最初は難しいと思うので、2次の対称行列をスペクトル分解してみて、射影\(P_i\)がどういうものか図示しながら考えてみてはいかがでしょうか。

一般的なベクトル\(x\)が固有空間によって分解できることが、対角化可能であることと同値であることも、そこから感じ取れると思います。

木村すらいむ（@kimu3_slime）でした。ではでは。