どうも、木村(@kimu3_slime)です。
高校数学の軌跡の問題では、「逆に、Bを満たす点はAを満たす」といった逆の確認をする回答が見られることがあります。
それはなぜ必要なのでしょうか、必ず書かなければならないことなのでしょうか。また、逆が成り立たない例もあります。それについて書きたいと思います。
逆の確認は必要か
「逆の確かめ」をしている回答例として、次の回答を引用しましょう。

画像引用:軌跡の方程式1 – 高校数学の基本問題
ここで、「逆に、\(y=x\)のとき……」といった確認は、どうして必要なのでしょうか。わかりやすくするために、
\[ \begin{aligned}命題P(x,y) : 点(x,y)は点A,Bからの距離が等しい\end{aligned} \]
\[ \begin{aligned}命題Q(x,y):点(x,y)はy=xを満たす\end{aligned} \]
と名前をつけてみましょう。
回答の前半で書かれていることは、\(P(x,y)\)を満たす点\((x,y)\)は\(Q(x,y)\)を満たすこと、すなわち\(P\)ならば\(Q\)を確かめているわけです。高校数学の論理の分野で学んだかと思いますが、一般に\(P\)ならば\(Q\)が成り立つからと言って、その逆\(Q\)ならば\(P\)が成り立つとは限りません。
軌跡の問題では、問題文に提示された\(P\)を満たすすべて点\((x,y)\)が求めたいものです。したがって、\(Q\)を満たす点を求めたからといって、それが本当に\(P\)と一致しているとは限らないのです。\(Q\)は満たすが\(P\)を満たさないような過剰な点を求めたのではなく、\(P\)を満たすすべての点を過不足なく求めましたよ、と宣言するために、逆の確認をしているわけですね。
ただし、おまじないのように「逆に~を満たす」と書いておけば良いというものではないでしょう。また、「逆に~と書かなければ間違い」とする指導案もあるようですが、それは妥当ではないです。
我が校には
・a²/³はダメ!a√aにしろ!
・f'(x)=0を解くとx=○なので…と書かないと減点!
・軌跡は逆に〜がないと問答無用で減点!
など謎ルールが幾つもあります
でも僕はそれを知った上で、いつもの答案の書き方を絶対に崩しません!悪魔に魂を売ってまでも点数を取りたいとは思わない!!!
— はなみや (@hanamiya_KU) July 12, 2021
数学の答案や回答では、逆が成り立っていることが明らかなケースでは、わざわざ「逆に」と断りを入れなくても正解でしょう。
例えば、\(x^2 -4x+3 =0\)を解けという問題で、\((x-1)(x-3)=0\)だから、\(x=1,3\)が解である、と答えるのは普通です。「逆に、\(x=1,3\)は\(x^2-4x+3=0\)を満たす」とわざわざ書かなくても良いのです。別に、書いても良いのですが、省略しても良いでしょう。
論理的には何をしているかといえば、「\((x-1)(x-3)=0\)ならば\(x=1,3\)」であり、「\(x=1,3\)ならば\((x-1)(x-3)=0\)」である、すなわち「\((x-1)(x-3)=0\)と\(x=1,3\)」は同値である(必要十分条件である)という議論をしているわけです。上から下に式だけを書いていくようですが、しばしばこの同値変形は省略されます。わざわざ逆が成り立つとかこの変形は同値であると宣言しなくても、支障がないケースはあります。
ただし、軌跡の問題では、少し気が緩むと同値でない変形をしてしまうことがあります。なので、「逆を確かめなさい」という指導がよくあるのでしょう。
それでも、同値変形であることを確認しているか、簡単な問題で明らかなケースならば、別に問題文の最後に「逆に」と書かなくても良いと思います。実際、Try it の軌跡の問題では、逆の確認をしていませんが、明らかでしょう。
上で見た問題ならば、ルートの部分を2乗する変形には注意が必要です。同値である記号\(\Leftrightarrow\)を使って
\[ \begin{aligned} &\sqrt{(x+1)^2+(y-3)^2}= \sqrt{(x-3)^2+(y-1)^2}\\&\Leftrightarrow& (x+1)^2+(y-3)^2=(x-3)^2+(y-1)^2\end{aligned} \]
と書いてあれば、この変形で逆が成り立つことをわかっているのだな、と読み取れます。なので、問題文の最後に「逆に」と書かなくても良いでしょう。
なぜこの同値関係が成り立つのかと言えば、両辺ともルートの中身\( (x+1)^2+(y-3)^2\),\((x-3)^2+(y-1)^2\)が常に0以上だからです。一般に、「\(\sqrt{a}= \sqrt{b}\)かつ\(a \geq 0,b\geq 0\)」は、「\(a=b\)」と同値です。
確認もせずなんでもかんでも「逆に」をつければ良いというものでもないのと同じように、とりあえず全部\(\Leftrightarrow\)をつければ良いというものではありません。論理記号を使うならば、論理的に正しく使わなければ減点されてしまうでしょう。当たり前のことですが。
逆が成り立たない例
逆が成り立たない例として、軌跡とは少しずれますが、次の問題を考えましょう。
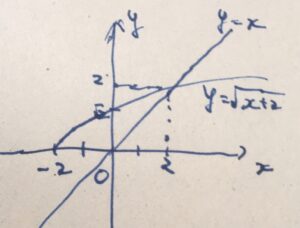
\(y=\sqrt{x+2}\)と\(y=x\)の交わる点\(x\)をすべて求めよ。
ありがちな誤答を書いてみます。
求める点は、\(\sqrt{x+2}=x\)を満たす。
\[ \begin{aligned}x+2 =x^2\end{aligned} \]
\[ \begin{aligned}x^2-x-2=0\end{aligned} \]
\[ \begin{aligned}(x+1)(x-2)=0\end{aligned} \]
\[ \begin{aligned}x=-1,2\end{aligned} \]
よって、求める点は\(x=-1,2\)である。
どこが間違いであるか指摘し、説明できるでしょうか?
気をつけなければならないのは、最初にルートを2乗した部分です。「\(\sqrt{x+2}=x\)ならば\(x+2=x^2\)」は正しいのですが、その逆「\(x+2=x^2\)ならば\(\sqrt{x+2}=x\)」は正しくないのです。ここは同値変形になっていません。
例えば上の回答に、「\(x=-1,2\)が条件を満たすか確認する。\(x=-1\)は\(\sqrt{1}=-1\)となって条件を満たさない。一方、\(x=2\)は条件を満たす。よって求める点は\(x=2\)である」と加わっていれば良いでしょう。この問題では、逆が成り立っているかどうかの確認が確かに必要ですね。
もっとも、図を書いて考えれば、\(x=-1\)で交わりようがないことにはすぐに気づけます。\(y=\sqrt{x+2}\)のグラフがどういうものか知っておく必要はありますが。図形がらみの問題では、できるなら図示をして、機械的に処理しすぎないことが間違いを減らすでしょう。
「\(\sqrt{x+2}=x\)」は「\(x+2=x^2\)かつ\(x+2 \geq 0\)かつ\(x \geq 0\)」と同値です。暗黙の前提ですが、軌跡や交点を求める問題では、\(x\)は複素数でなく実数であると考えています。実数\(x\)に対して、\(\sqrt{x+2}=x\)という式があったら、右辺が実数なので左辺も実数であり、ルートの中身が正であること\(x+2 \geq 0\)が導かれます。また、\(\sqrt{}\)記号は正の平方根を表すので、\(x \geq 0\)も仮定されています。
つまり、単に\(x+2 =x^2\)を解くだけではなく、それを満たす\(x\)のうち\(x+2 \geq 0\)かつ\(x \geq 0\)を満たすものを見つけなければ、条件を勝手に緩めることになってしまいます。\(x=-1,2\)のうち\(x\geq 0\)を満たすのは\(x=2\)のみであり、それが求める点というわけです。
一般に「\(a=b\)ならば\(a^2 =b^2\)」は正しいですが、その逆「\(a^2 =b^2\)ならば\(a=b\)」は正しくありません。例えば、\(a=1,b=-1\)のときを考えると、\(a^2=b^2=1\)ですが、\(a\neq b\)なので。
このように、2乗をする・ルートを取る操作は同値変形にならないことがあるので、気をつけましょう。条件を加えて「\(a=b\)」と「\(a^2=b^2\)かつ\(a \geq 0 , b \geq 0\)」は同値です。
ルートや絶対値、対数に関する問題では、式変形のときに登場している文字が正かどうかの確認が必要になることが多いです。
最大値や最小値、極値の問題でも、逆が成り立つかどうかには注意が必要になります。
以上、軌跡の問題で逆の確認が必要かどうか、逆が成り立たない例を紹介してきました。
「最後に逆も成り立つ」と書いておけば良いという考えだと、その場しのぎで簡単な問題は一応合ってる回答にはなりますが、実際に逆が成り立たない問題でそう書いてしまう可能性があります。
今回紹介したような、2乗によって同値関係が保たれたり崩れる例を考えて、逆が成り立つ・確かめるとはどういうことなのか理解してみてはいかがでしょうか。
普段から「\(P\)ならば\(Q\)」の変形なのか、「\(P\)と\(Q\)は同値である」という逆も成り立つ変形なのか、論理を意識しましょう。そうすると、正確に数学を理解でき、自信を持って答案を書けるようになるでしょう。
木村すらいむ(@kimu3_slime)でした。ではでは。
旺文社 (2018-09-18T00:00:01Z)
¥4,972 (コレクター商品)
こちらもおすすめ
「AならばB」のよくある誤解から学ぶ、論理学入門(対偶、逆、否定、真偽表)