シュミットの直交化法とは：正規直交基底の具体的な求め方

どうも、木村（@kimu3_slime）です。

互いに直交している基底があると、線形空間を分析するのにとても便利です。

今回は、正規直交基底の具体的な求め方として、シュミットの直交化法を紹介します。

正規直交基底とは
シュミットの直交化法とは
こちらもおすすめ

正規直交基底とは

例えば、3次元ユークリッド空間\(\mathbb{R}^3\)において、\(e_1 =(1,0,0)\)、\(e_2 =(0,1,0)\)、\(e_3=(0,0,1)\)は、それぞれ直交していて（内積が0）、かつ基底でもあります。

互いに直交していて基底であるベクトルの組を、正規直交基底（orthonormal basis）と呼びます。

一般に、直交しているベクトル同士は互いに線形独立です。したがって、\(n\)次元の線形空間では、直交しているベクトルを何本も見つけられれば、それらが基底とわかります。

参考：直交ベクトルの線形独立性、直交行列について解説

さきほど取り上げた\(e_1,e_2,e_3\)のような、ある成分が1で他が0であるような正規直交基底は、標準基底と呼ばれます。

しかし、一般の正規直交基底は標準基底のように単純であるとは限りません。例えば、\(\frac{1}{\sqrt{2}}(1,1),\frac{1}{\sqrt{2}}(1,-1)\)は\(\mathbb{R}^2\)の正規直交基底です（図を書きつつ、確かめてみてください）。

一般に、\(V\)を有限次元の内積空間としましょう。そこには\(a_1,\dots,a_n\)という何らかの基底がありますが、一般に正規直交であるとは限りません。しかし、そこから必ず正規直交基底を作り出すことができます。それが今回紹介する、シュミットの直交化法です。

例えば、直交補空間の議論をするときには、内積空間から正規直交基底を取ってきて議論しています。こうした強力な議論ができるのは、シュミットの直交化のおかげです。

参考：直交補空間、直交直和、直交射影とは：定義と例、証明

シュミットの直交化法とは

シュミットの直交化法は、線形独立なベクトル\(a_1,\dots,a_n\)から、直交なベクトル\(b_1,\dots, b_n\)を作り出し、それを正規化（大きさを1にする）して\(c_1,\dots,c_n\)という正規直交基底を得る方法です。

\[ \begin{aligned}b_k =a_k – \sum_{i=1}^{k-1}\langle c_i,a_k \rangle c_i \end{aligned} \]

\[ \begin{aligned}c_k = \frac{1}{\|b_k\|} b_k\end{aligned} \]

一般形をいきなり見ても発想がわからないと思うので、まずは具体的にやってみましょう。

具体例1

まずは\(\mathbb{R}^2\)において、\(a_1= (0,1)\)、\(a_2 =(1,1)\)を正規直交化してみましょう。これらのベクトルは線形独立です。

状況を図に書いてみます。

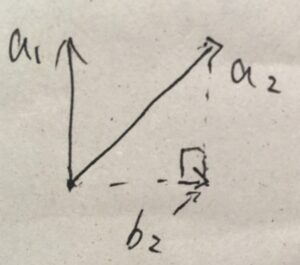
\(a_1\)の大きさは1であり、既に正規化されています。そこで、\(b_1 := a_1\)はそのまま使いましょう。

続いて、\(b_1\)に直交するベクトル\(b_2\)を求めたいです。まず、\(b_2\)を未知のベクトルとします。そして、\(b_1=a_1\)を定数倍することで、\(kb_1+b_2 = a_2\)と表せないか考えてみましょう。

幾何学的には、\(a_2\)の\(b_2\)への直交射影を求めています。\(b_2\)とは、\(a_1\)の張る線形空間（直線）の直交補空間のベクトルです。

まあ、今回は図から\(k=1\)で良いじゃないかとわかってしまいます（笑）。一般的な方法を考えるならば、\(b_1,b_2\)は直交しているという条件があるわけです。

\(b_2 =a_2- kb_1\)において\(b_1\)との内積を取れば、左辺は\( \langle b_1 ,b_2\rangle=0\)、右辺は\( \langle b_1,a_2 \rangle -\langle k b_1, b_1\rangle =\langle b_1,a_2 \rangle -k\)です（\(b_1\)の大きさは1なので）。したがって、\(k= \langle b_1,a_2 \rangle \)となりました。

具体的に計算すれば、\(k=0+1=1\)です。よって、\(b_2 = a_2 -k b_1 =(1,1)-(0,1)=(1,0)\)とすれば、\(b_1,b_2\)は直交します。また、（たまたまですが）\(b_2\)の大きさは1なので、\(b_1,b_2\)が正規直交基底であるとわかりました。

具体例2

\(\mathbb{R}^3\)において、

\[ \begin{aligned}a_1,a_2,a_3 =\begin{pmatrix} 1\\ 2 \\1\end{pmatrix},\begin{pmatrix} 2\\ 1 \\2\end{pmatrix}, \begin{pmatrix} 2\\ 1 \\1\end{pmatrix}\end{aligned} \]

を正規直交化してみましょう。これらは線形独立です。

参考：線形独立・従属の判定法：行列のランクとの関係

画像引用：WolframAlpha

流れとしては、正規化、直交化、正規化……と交互に作成していきます。

まず、記号の都合上、\(b_1 =a_1\)と置きましょう。\(b_1\)の大きさは1ではないですが、\(c_1 = \frac{1}{\|b_1\| }b_1\)と置けば正規化できます。

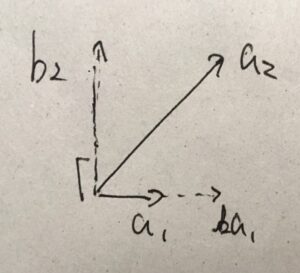
続いて、\(c_1\)と直交するベクトル\(b_2\)を作りましょう。

\(c_1\)が張る線形空間（直線）に直交するベクトルが\(b_2\)です。\(a_2\)から\(b_2\)への射影を求めたいわけです。

もしそういう\(b_2\)があるなら、\(c_1\)の長さを調整すれば、\(a_2 =kc_1 +b_2\)と表せるわけです。そして、\(c_1,b_2\)は直交していることに気をつけて、内積を使って整理しましょう。

両辺で\(c_1\)との内積を取れば、\(\langle c_1,a_2 \rangle = k\langle c_1,c_1 \rangle+0 =k\)です。

よって、\(b_2 =a_2-kc_1 = a_2 -\langle c_1,a_2 \rangle c_1\)と求められました。大きさは1とは限らないので、\(c_2 = \frac{1}{\|b_2\|} b_2\)と正規化します。

続いて、\(c_1,c_2\)に対して直交するベクトル\(b_3\)を、\(a_3\)を使って表してみましょう。

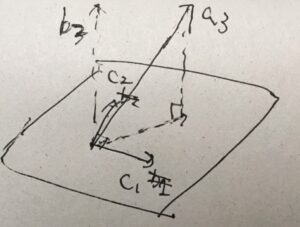
幾何学的に考えると、直交するベクトル\(c_1,c_2\)はひとつの平面を張っています。それに対して直交するベクトル\(b_3\)を\(a_3\)を使って表したいです。

\(c_1,c_2\)が張る線形空間は、平面です。その直交補空間のひとつの要素が、求めたい\(b_3\)となります。\(a_3\)を\(b_3\)に射影、\(c_1,c_2\)が張る線形空間の直交補空間に射影したいわけです。

平面上のベクトルは、2つの定数\(k_1,k_2\)を使って\(k_1c_1+k_2 c_2\)と線形結合で表せます。長さを調整して、\(k_1 c_1 +k_2 c_2 +b_3 =a_3\)となるような\(b_3\)を求めたいわけです。

\(b_3\)は\(c_1,c_2\)と直交しているという条件から、\(k_1,k_2\)が求められます。等式において\(c_1,c_2\)との内積を取れば、直交する項は消えて

\[ \begin{aligned}k_1\langle c_1,c_1\rangle =\langle c_1,a_3\rangle\end{aligned} \]

\[ \begin{aligned}k_2\langle c_2,c_2\rangle =\langle c_2,a_3\rangle\end{aligned} \]

となります。

よって、\(b_3 =a_3 -\langle c_1,a_3\rangle a_1 – \langle c_2,a_3\rangle c_2\)とすれば、\(c_1,c_2,b_3\)は直交します。\(c_3 = \frac{1}{\|c_3\|}\)とすれば、\(c_1,c_2,c_3\)という正規直交基底が得られました。

では、\(c_1,c_2,c_2\)を具体的に求めてみましょう。計算ミスしやすいので、できるだけ文字のまま扱う工夫が大事です。

\[ \begin{aligned}a_1,a_2,a_3 =\begin{pmatrix} 1\\ 2 \\1\end{pmatrix},\begin{pmatrix} 2\\ 1 \\2\end{pmatrix}, \begin{pmatrix} 2\\ 1 \\1\end{pmatrix}\end{aligned} \]

\[ \begin{aligned}b_1 =a_1\end{aligned} \]

\[ \begin{aligned}c_1 =\frac{1}{\|b_1\|} b_1 =\frac{1}{\sqrt{6}}\begin{pmatrix} 1\\ 2 \\1\end{pmatrix}\end{aligned} \]

\[ \begin{aligned} b_2 &=a_2-\langle c_1,a_2\rangle c_1 \\ &=\begin{pmatrix} 2\\ 1 \\2\end{pmatrix} -(\frac{1}{\sqrt{6}}\begin{pmatrix} 1\\ 2 \\1\end{pmatrix}\cdot \begin{pmatrix} 2\\ 1 \\2\end{pmatrix})\frac{1}{\sqrt{6}}\begin{pmatrix} 1\\ 2 \\1\end{pmatrix} \\&= \begin{pmatrix} 2\\ 1 \\2\end{pmatrix}- \begin{pmatrix} 1\\ 2 \\1\end{pmatrix}\\&= \begin{pmatrix} 1\\ -1 \\1\end{pmatrix} \end{aligned} \]

\[ \begin{aligned}c_2 =\frac{1}{\|b_2\|}b_2 = \frac{1}{\sqrt{3}}\begin{pmatrix} 1\\ -1 \\1\end{pmatrix} \end{aligned} \]

\[ \begin{aligned} b_3 &=a_3 -\langle c_1,a_3\rangle a_1 – \langle c_2,a_3\rangle c_2 \\ &= \begin{pmatrix} 2\\ 1 \\1\end{pmatrix}- (\frac{1}{\sqrt{6}}\begin{pmatrix} 1\\ 2 \\1\end{pmatrix}\cdot \begin{pmatrix} 2\\ 1 \\1\end{pmatrix})\frac{1}{\sqrt{6}}\begin{pmatrix} 1\\ 2 \\1\end{pmatrix} \\ &-(\frac{1}{\sqrt{3}}\begin{pmatrix} 1\\ -1 \\1\end{pmatrix} \cdot \begin{pmatrix} 2\\ 1 \\1\end{pmatrix} ) \frac{1}{\sqrt{3}}\begin{pmatrix} 1\\ -1 \\1\end{pmatrix} \\ &= \begin{pmatrix} 2\\ 1 \\1\end{pmatrix} -\frac{5}{6}\begin{pmatrix} 1\\ 2 \\1\end{pmatrix} – \frac{2}{3}\begin{pmatrix} 1\\ -1 \\1\end{pmatrix} \\&=\frac{1}{6}\left( \begin{pmatrix} 12\\ 6 \\6\end{pmatrix} – \begin{pmatrix} 5\\ 10 \\5\end{pmatrix}-\begin{pmatrix} 4\\ -4 \\4\end{pmatrix} \right)\\&= \frac{1}{2}\begin{pmatrix} 1\\ 0 \\-1\end{pmatrix} \end{aligned} \]

\[ \begin{aligned}c_3 =\frac{1}{\|b_3\|}b_3 =\frac{1}{\sqrt{2}} \begin{pmatrix} 1\\ 0 \\-1\end{pmatrix} \end{aligned} \]

実際、\(c_1,c_2,c_3\)は正規直交基底になっています（検算として、確かめてみてください）。

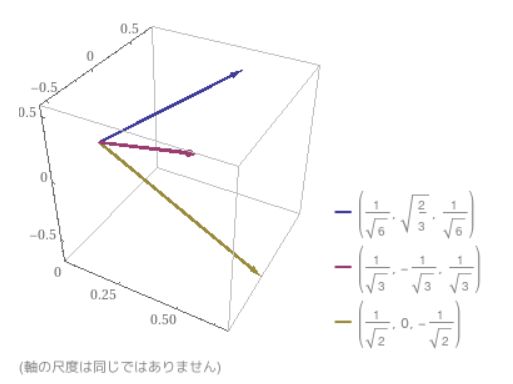
画像引用：WolframAlpha

一般形

今までの議論をまとめれば、次のような一般形が得られることはすぐに予想できるでしょう。

\(a_1,\dots,a_n\)を線形独立なベクトルとします。

\[ \begin{aligned}b_1 :=a_1\end{aligned} \]

\[ \begin{aligned}c_1 := \frac{1}{\|b_1\|}b_1\end{aligned} \]

\[ \begin{aligned}b_2 =a_2 -\langle c_1,a_2 \rangle c_1\end{aligned} \]

\[ \begin{aligned}c_2 =\frac{1}{\|b_2\|} b_2\end{aligned} \]

\[ \begin{aligned}b_k =a_k – \sum_{i=1}^{k-1}\langle c_i,a_k \rangle c_i \end{aligned} \]

\[ \begin{aligned}c_k = \frac{1}{\|b_k\|}b_k\end{aligned} \]

と定めていけば、正規直交基底\(c_1,\dots,c_n\)が得られます。これをグラム・シュミットの直交化法（Gram–Schmidt process）と呼びます。

\(c_1,\dots,c_n\)の大きさが1であること、正規化されていることは明らかでしょう。そこで、それらが直交していることを数学的帰納法で証明します。係数は直交性に影響しないので、\(b_1,\dots ,b_n\)の直交性を調べれば十分です。

最初のケースとして、\(b_1,b_2\)の直交性を調べます。内積の線形性を使って、

\[ \begin{aligned} \langle b_1,b_2\rangle&= \langle b_1 ,a_2 -\langle c_1,a_2 \rangle c_1 \rangle \\ &= \langle b_1 ,a_2 \rangle -\langle c_1,a_2 \rangle\langle b_1,c_1 \rangle \\ &= \langle b_1 ,a_2 \rangle – \frac{1}{\|b_1\|}\langle b_1,a_2 \rangle \frac{1}{\|b_1\|}\langle b_1,b_1 \rangle\\ &= \langle b_1 ,a_2 \rangle – \langle b_1 ,a_2 \rangle \\&= 0\ \end{aligned} \]

と直交性が示せました。続いて、\(b_1,\dots,b_{k-1}\)が直交しているとして、\(b_k\)との直交性を調べましょう。一般的に、\(b_j\),\(1 \leq j \leq k-1\)との内積を計算します。

\[ \begin{aligned} \langle b_j,b_k\rangle&= \langle b_j ,a_k – \sum_{i=1}^{k-1}\langle c_i,a_k \rangle c_i \rangle \\ &= \langle b_j ,a_k \rangle -\sum_{i=1}^{k-1}\langle c_i,a_k \rangle\langle b_j,c_i \rangle\\ &= \langle b_j ,a_k \rangle -\langle c_j,a_k \rangle\langle b_j,c_j \rangle \\ &= \langle b_j ,a_k \rangle – \frac{1}{\|b_j\|}\langle b_j,a_k \rangle \frac{1}{\|b_j\|}\langle b_j,b_j \rangle\\ &= \langle b_j ,a_k \rangle – \langle b_j ,a_k \rangle \\&= 0\ \end{aligned} \]

となり、正規直交基底であることがわかりました。

幾何学的には、シュミットの直交化法は、直交補空間への射影を取り続けるプロセスです。

まず、\(a_1\)を正規化した\(c_1\)から出発します。\(c_1\)の生成する直線を\(W_1 := \mathrm{span}(c_1)\)と表しましょう。部分空間に対しては、それに直交するベクトルを集めた空間：直交補空間が存在します。

\(b_2=a_2 -\langle c_1,a_2 \rangle c_1\)と置くと、\(c_1,b_2\)は直交していて、すなわち\(b_2 \in W_1 ^\perp\)となっています。\(a_2 =\langle c_1,a_2 \rangle c_1 +b_2\)で、\(c_1 \in W_1\)、\(b_2 \in W_1 ^\perp \)を満たしているので、\(b_2\)を\(a_2\)の\(W_1 ^{\perp}\)への直交射影というのでした。

そして、正規化して\(c_2\)と置きましょう。\(W_2:= \mathrm{span}(c_1,c_2)\)と置いて、\(a_3\)の直交補空間\(W_2^\perp\)への射影\(b_3\)を求める。これを繰り返すわけです。

\(W_{k-1}:= \mathrm{span}(c_1,\dots,c_{k-1})\)と置くと、\(W_{k-1}\)は\(k-1\)次元の部分空間です。\(b_k =a_k – \sum_{i=1}^{k-1}\langle c_i,a_k \rangle c_i\)と置くと、\(b_k\)は\(a_k\)の\(W_{k-1}^\perp\)への射影（直交射影）となるわけです。

仮定の\(a_1,\dots,a_k\)が線形独立であることは必要です。線形独立でないと、途中で直交補空間が0次元になり、直交するベクトルが見つけられなくなってしまいます。

以上、正規直交基底の求め方として、シュミットの直交化法を紹介してきました。

内積空間では、線形独立なベクトルがあれば、それらを正規直交化することができます。数ベクトル空間だけでなく、多項式のなす空間で基底から直交基底（直交多項式）を考えることもあります。フーリエ級数展開も、直交基底の重要な応用例です。

シュミットの直交化法は、ユークリッドの互除法のように、理論的にも役立ちますし、実際の計算の手順も与えてくれる優れた方法です。その幾何学的な発想も難しくないので、ぜひ意味を考えながら計算できるようになってみてください。

木村すらいむ（@kimu3_slime）でした。ではでは。