環、体とは何か：数、多項式、行列、Z/nZを例に

どうも、木村（@kimu3_slime）です。

今回は、大学数学で見かける用語、環、体とは何かについて、数、多項式、行列、Z/nZを例に紹介します。

細かく証明はしません。環や体という用語にビビらないようにするための展望を得たい人向け。お話寄りです。

集合の初歩の知識があると良いでしょう：集合論入門：集合の定義、数の集合、ラッセルのパラドックス

環、体とは何か

数のなす環、体

環（かん）や体（たい）とは、簡単に言えば、足し算や掛け算ができるような集合のことです。

中学数学から馴染みのある有名な例としては、整数環\(\mathbb{Z}\)、実数体\(\mathbb{R}\)などがあります。

体という概念は、例えば微積分の基礎（実数とは連続性の公理を満たす順序体）として、杉浦「解析入門 Ⅰ」に登場します。また、齋藤「線型代数入門」では、線形空間（ベクトル空間）のスカラーの役割をする集合として、実数体\(\mathbb{R}\)や複素数体\(\mathbb{C}\)という係数体を考えています。それを一般化した記号として\(\mathbb{K}\)を使っていて、そうした数の集合を一般化した概念として体（や環）があります。

例えば、実数\(\mathbb{R}\)は単に数の集まりではなく、いくつかの「数学的構造」を備えています。その構造は主に3種に分類されます。

位相的構造：近さを考え、距離を測ることができる
代数的構造：足し算や掛け算、四則演算ができる
順序構造：数を不等号で比較できる

このうち、環や体と呼ばれるものは、代数的構造に分類され、計算の規則に注目するものです。

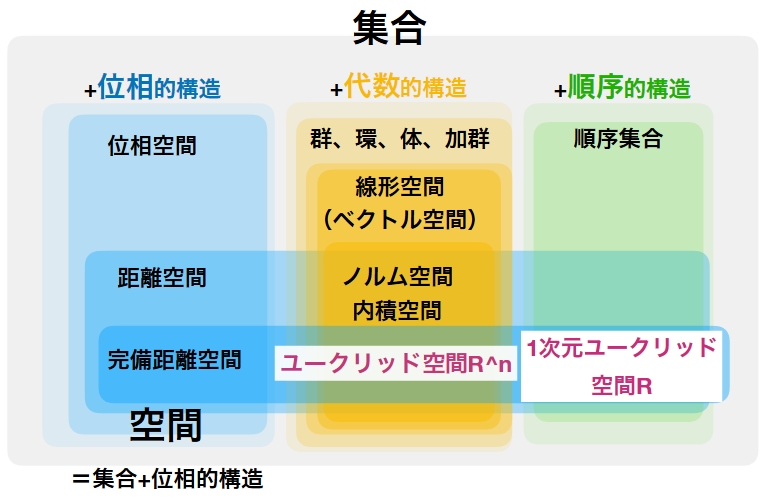
参考：集合、構造、空間とは何か？ユークリッド空間R^Nを例に考える

環、体の定義

環や体は、整数や実数が持っているような計算法則を一般化したものです。より形式的に言えば、集合と2つの2項演算のセットのことです。

まず、環の定義を見ていきましょう。

\(R\)を集合とする。

\(R\)に加法\(+\)と乗法\(\cdot\)という2項演算が定義され、次の条件を満たすとする。

加法について可換群をなす
- 結合法則：\(a,b,c \in R\)に対し、\(a+(b+c)=(a+b)+c\)
- 単位元の存在：次の条件を満たす\(0_R \in R\)が存在する。\(a \in R\)に対し、\(a+0_R =a\)
- 逆元の存在：\(a \in R\)に対し、\(a+b=0_R\)を満たす\(b\in R\)が存在する。\(b\)を\(a\)の加法逆元（マイナス）と呼び、\(b=-a\)と書く。
- 交換法則：\(a,b \in R\)に対し、\(a+b=b+a\)
乗法について
- 結合法則：\(a,b,c \in R\)に対し、\((ab)c=a(bc)\)
- 単位元の存在：次の条件を満たす\(1_R \in R\)が存在する。\(a \in R\)に対し、\(1_R a = a 1_R=a\)
分配法則：\(a,b,c \in R\)に対し、\(a(b+c)=ab+ac\)、\((b+c)a=ba+ca\)

このとき、\(R\)を環（ring）という。\(0_R\)を加法単位元、\(1_R\)を乗法単位元という。

長い定義で、びっくりしたかもしれません。言っていることを噛み砕いて要約しましょう。

まず、舞台となる集合\(R\)があります。そして、「その集合の中で」足し算と掛け算が定義できると言っています。特に、\(0_R ,1_R\)といった、足し算や掛け算に影響を与えない特別な要素（単位元）を持っています。さらに、引き算もできるといっています（逆元の存在）。そして、足し算と掛け算を両立させる法則、分配法則が成り立つと。

整数の集合\(\mathbb{Z}\)は、通常の足し算・掛け算について、環をなしています。上で述べた定義は、整数の計算のルールとして中学校で学んだものでしょう。加法単位元は\(0\)、乗法単位元は\(1\)です。これを整数環（integer ring）と呼びます。

環でない例としては、自然数の集合\(\mathbb{N}\)があります。同様の足し算、掛け算を考えましょう。\(\mathbb{N}\)は和について閉じていません。例えば、\(2-3 \not \in \mathbb{N}\)です。このように計算の結果が集合の外側にはみ出てしまうときは、環とは呼べません。環と呼ぶときは、和と積について閉じているのです。

環でないことを正確に言えば、例えば\(3\)には逆元が存在しません。\(n+3=0\)となるような\(n\in \mathbb{N}\)は存在しないのです。環というのは、マイナスを考えることができる世界です。

「～は環である」というとき、それは「（2つの演算について）環である」ことの省略であることに注意しよう。単に「\(R\)を環とする」と言ったりしますが、そこでは演算：和と積\(+,\cdot\)が暗黙のうちに想定されています。

環では足し算と掛け算ができます。しかし、（あまりのない）割り算がいつでもできるとは限りません。割り算ができるような環を、体と呼びます。

\(R\)を環とする。

乗法について群をなす
- 逆元の存在：\(0_R\)でない任意の\(a \in R\)に対し、\(ab =ba =1_R\)を満たす\(b \in R\)が存在する。\(b\)を\(a\)の乗法逆元（逆数）と呼び、\(b=a ^{-1}\)と書く。

このとき、\(R\)を体（field）と呼ぶ。

有理数\(\mathbb{Q}\)、実数\(\mathbb{R}\)、複素数\(\mathbb{C}\)では、それぞれ数について割り算を行うことができ、体をなしています。それぞれ、有理数体（rational field）、実数体（real field）、複素数体（complex field）と呼びます。

\(\mathbb{Z}\)は体にはなりません。例えば、\(2\)の乗法逆元が存在しないからです。\(2 x =1\)となるような整数\(x \in \mathbb{Z}\)は存在しませんね。

体は、加減乗除ができる集合のことです。環は必ずしも割り算がでなくてもよく、加減乗ができる集合ですね。集合\(R\)は体であるならば環でもありますが、逆は成り立ちません。

（整数のような環では、あまりのある割り算なら必ず考えることができます。整数のようにあまりのある除法を考えられる環は、一般にユークリッド整域と呼ばれるものです。）

環は\(R\)、体は\(F\)または\(K,\mathbb{K}\)という記号を使って使って書くことが多いです。これは英語のring、fieldから取っているのだろう。Kは、ドイツ語で体を意味するKörperから取っていると思われます。日本語訳である体も、おそらくこちらに由来するのでしょう。環も体も、その要素を組み合わせて有機的に計算できる舞台、というようなニュアンスだと思います。

多項式環

環の例は、数の集まりだけではありません。その例をいくつか紹介していきます。

\(\mathbb{R}[x]\)を実数係数の多項式のなす集合とします。例えば、\(3x+2 \in \mathbb{R}[x]\)です。

高校数学で学ぶように、多項式同士の和は多項式になりますし、多項式同士の積もまた多項式になります。つまり、\(\mathbb{R}[x]\)は環です。

\[ \begin{aligned}f=\sum_{i=0} a_i x^i,g= \sum _{i=0} b_i x^i\end{aligned} \]

\[ \begin{aligned}f+g:= \sum _{i=0} (a_i+b_i)x^{i}\end{aligned} \]

\[ \begin{aligned}fg :=\sum_{i=0}(\sum_{j=0}^i a_j b_{i-j})x^{i}\end{aligned} \]

一般に、環\(R\)の要素を係数とする多項式のなす集合\(R[x]\)は、和と積について環となります。これを多項式環（polynomial ring）と呼びます。

（より厳密には、多項式とは何かをきちんと定義する必要があるでしょう。例えば\(3x+2 \)は0次の係数が2、1次の係数が3、2次以降の係数はすべて0です。これを\((2,3,0,\dots)\)という数列に対応させることができます。つまり、多項式は係数を表す数列で、0でないものが有限項であるものとして定義します。）

抽象代数学では、\(R[X]\)のように、多項式の変数を大文字\(X\)で書く習慣もよく見ます。\(X\)を多項式用の特別な変数記号として使い、それに特殊な値を入れた結果を\(x\)と小文字で表したいからでしょう。

また、実数体と多項式環から、多項式環の商環\(\mathbb{R}[x]/(x^2+1)\)として複素数体を構成できることが知られています。つまり、複素数体は、実数体に\(x^2+1=0\)の解：虚数単位をつけたした（添加した）拡大体として見れます。

多項式環の世界は奥深いです。代数的整数論やガロア理論にもつながる重要な例と言えます。

参考：群論からガロア理論への入門（五次方程式の解の公式は存在しない）

行列環

実数を成分とする\(n\)次の正方行列のなす集合\(M(n,\mathbb{R})\)について考えましょう。

参考：行列全体のなす集合が線形空間（ベクトル空間）となることの証明

正方行列同士の和は正方行列、積も正方行列です。\(A\)に対して\(-A\)も定まりますし、ゼロ行列\(O\)が加法単位元、単位行列\(I\)は乗法単位元となります。つまり、\(M(n,\mathbb{R})\)は環です。

一般に、体\(K\)を成分とする\(n\)次の正方行列のなす集合\(M(n,\mathbb{K})\)を行列環（matrix ring）と呼びます。

2次以上の行列環では、積は可換とは限りません。

\[ \begin{aligned}R=\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}\end{aligned} \]

\[ \begin{aligned}F=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\end{aligned} \]

という行列を考えると、\(RF \neq FR\)です（回転行列と反転行列は可換ではない）。

参考：回転行列とは？導出と例、性質を紹介、図形の対称性を記述する二面体群、多面体群、点群・結晶群について解説

一般に、環\(R\)が交換法則\(ab =ba\)を満たすとき、それは可換環（commutative ring）と呼ばれます。

満たさないときは、非可換環（noncommutative ring）です。行列環は、非可換環の有名な例と言えます。そもそも環の定義において、加法で可換性を仮定し、乗法でその条件を課さなかったのは、行列環のような非可換環を考えたいから、という面があるわけです。

剰余類環 Z/nZ

最後に紹介する環の例が、整数の剰余類環\(\mathbb{Z} /n\mathbb{Z}\)です。

\(n=3\)として考えてみます。整数を\(3\)で割ったあまりは、\(0,1,2\)のいずれかです。そこで、\(3\)で割ったあまりが\(0\)であるような整数をまとめて（同一視）して\([0]\)といったように書きます。

あまりが等しい数を合同と考える計算は、合同算術と呼ばれるものです。

参考：同値関係、2項関係とは？整数の合同（mod）を例に

参考：商集合、同値関係・同値類を解説～商群の理解に向けて、群論入門～回転群と巡回群を例に、群の定義・同型・位数を解説

合同算術によって、整数の集合からあまりをまとめた集合

\[ \begin{aligned}\mathbb{Z} / 3\mathbb{Z}:=\{[0],[1],[2]\}\end{aligned} \]

\[ \begin{aligned}\mathbb{Z} / n\mathbb{Z}:=\{[0],[1],\dots,[n-1]\}\end{aligned} \]

が定義できます。そして、これらに対して和と積が問題なく定義できます。

\[ \begin{aligned}[k]+[\ell] := [k+\ell]\end{aligned} \]

\[ \begin{aligned}[k]\cdot[\ell] := [k \ell]\end{aligned} \]

こうして定まる環\(\mathbb{Z} /n\mathbb{Z}\)を、nを法とする整数の剰余類環（residue ring modulo n）と呼びます。\(\mathbb{Z}_n\)と書くことも。

（詳しくは、代表元によらず和、積が定義できているかのチェックが必要です：well-definedとは：代表元の取り方によらない確認はなぜ必要か）

この環では、プラスの数を有限回足していくと結果が0になるようなことが起こります。乗法単位元\(1_R\)を複数回足していってゼロになるような個数のことを、標数（characteristic）といいます。\(\mathbb{Z} /n\mathbb{Z}\)の標数は\(n\)です。普通の数\(\mathbb{Z},\mathbb{Q},\mathbb{R},\mathbb{C}\)のなす環の標数は、\(0\)と考えます。

法が素数\(n=p\)のときは、\(\mathbb{Z} /p\mathbb{Z}\)は体にもなります。一般に、\(n\)を法として\(a\)が乗法逆元（逆数）を持つ必要十分条件は、\(n,a\)が互いに素であることです。法が素数のとき、\(\mathbb{Z} /p\mathbb{Z}\)のすべての0でない要素が逆数を持つことになります。

この体を \(F_p: =\mathbb{Z} /p\mathbb{Z}\)と表すことがあります。要素が有限個の体は有限体（finite field）と呼ばれ、通信や暗号の理論に応用されているようです。

加群と線形空間

最後に、環や体をベースにした代数的構造、加群について触れておきましょう。それは線形空間（ベクトル空間）のようなものです。

\(R\)を環、\(M\)を加法群とする。

スカラー倍と呼ばれる二項演算：\(R\times M \to M\)で、

\(a\in R,x,y\in M\)ならば、\(a(x+y)=ax+ay\)
\(a ,b \in R,x \in M\)ならば、\((a+b)x =ax+bx\)
\(a ,b \in R,x \in M\)ならば、\((ab)x =a(bx)\)
\(x \in M\)ならば、\(1_R x =x\)

を満たすとき、\(M\)は\(R\)上の加群（module）と呼ぶ。

環や体を係数として使って考えられる構造が、加群です。係数\(R\)が体\(\mathbb{K}\)のとき、\(\mathbb{K}\)-線形空間（ベクトル空間 linear space）と呼ばれます。\(\mathbb{K}\)が\(\mathbb{R}\)なら実線形空間、\(\mathbb{C}\)なら複素線形空間です。

加群とは、係数が体でないケースのときの線形空間の一般化です。多次元のユークリッド空間\(\mathbb{R}^N\)が線形空間であるように、環\(R\)を使って\(R^N\)という加群を考えることができます。線形代数学とは、体上の加群の理論、という側面があるわけです。

以上、環、体とは何か、数、多項式、行列、Z/nZを例に紹介してきました。

定義は少し難しかったかもしれませんが、要は足し算や掛け算ができるような集合に名前がついている、というだけのことです。

足し算や掛け算が考えられるような対象、数に限らず多項式や行列のようにたくさんあって、一見違うように見えるものが同じ抽象的な定義を満たす対象と見れるのは驚きではないでしょうか。今回の話が、抽象代数学、環や体という言葉の便利さを感じるきっかけとなれば嬉しいです。

木村すらいむ（@kimu3_slime）でした。ではでは。