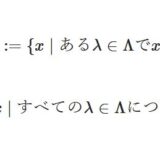どうも、木村(@kimu3_slime)です。
位相空間の定義のひとつに、開集合系の性質を用いたものがあります。
その定義に納得するためには、ユークリッド空間における開集合、閉集合の性質について知っておくと良いでしょう。今回はそれを紹介します。
開集合、閉集合の具体例
開集合とは、境界を持たない、開いた集合のことです。ユークリッド空間\(\mathbb{R}^N\)において\(A\)が開集合であるとは、すべての点\(x\in A\)に対して\(B(x,\varepsilon )\subset A\)となるような開球\(B(x,\varepsilon )\)が存在することです。
閉集合とは、境界をすべて含んだ、閉じた集合のことです。\(A\)が閉集合であるとは、その補集合\(\mathbb{R}^N \backslash A\)が開集合であることです。
詳しくは:ユークリッド空間の開集合、閉集合、開球、近傍とは何か?
今回考えたいのは、以下のような性質です。
- \(\mathbb{R}^N\)、\(\varnothing \)は開集合。
- \((U_\lambda)_{\lambda \in \Lambda}\)を任意の開集合族とするとき、和集合\(\bigcup _{\lambda \in \Lambda} U_\lambda\)は開集合。
- \(U_1,\dots, U_n\)を有限個の開集合とするとき、共通部分\(\bigcap _{i=1} ^n U_i\)は開集合。
まずはこれが成り立っているかどうか、実数\(\mathbb{R}\)の区間による具体例を考えて、実験してみましょう。
1.全体集合、空集合が開集合であるのは、ほぼ当たり前なので置いておきます。
2.について。\(A_\lambda = (\lambda -\frac{1}{10},\lambda + \frac{1}{10})\)、\(\lambda \in [0,1]\)は非可算無限個の開集合族です。そして、その和集合は\(\bigcup _{\lambda \in [0,1]} A_\lambda = (-\frac{1}{10},1+ \frac{1}{10})\)であり、確かに開集合になっています。
3.について。\(B_i = (0,\frac{1}{i})\)という開集合を考えましょう。その添字が\(i=1,\dots,n\)のときは、\(\bigcap_{i=1}^n B_{i} =(0,\frac{1}{n})\)であり、確かに開集合です。しかし、無限個の和、\(i \in \mathbb{N}\)とすると、\(\bigcap_{i\in \mathbb{N}} B_{i} =\{0\}\)となります。これは開集合ではありません(どんなに小さな開球を考えても、一点に含まれることはない)。一般に、一点集合は開集合ではありません。
つまり、開集合の有限個の共通部分は必ず開集合ですが、無限個の共通部分は必ずしも開集合ではありません。
ちなみに、一点集合は常に閉集合です。しかし、閉集合だから開集合でない、と主張するのは誤り(議論に飛躍あり)です。非常によくある間違いなので気をつけましょう。一点集合は開集合でないという結論自体は正しいですが。
開集合と閉集合は似た定義をしているものの、相互に独立です。全体集合や空集合は、開集合であり、かつ閉集合になります。また、半開区間\([0,1)\)は開集合でも閉集合でもありません。「すべての集合は、開集合または閉集合のいずれかである」と排他的にイメージすることは、間違いとなります。
開集合、閉集合の性質
では、開集合の一般的な性質を証明してみましょう。
- \(\mathbb{R}^N\)、\(\varnothing \)は開集合。
- \((U_\lambda)_{\lambda \in \Lambda}\)を任意の開集合族とするとき、和集合\(\bigcup _{\lambda \in \Lambda} U_\lambda\)は開集合。
- \(U_1,\dots, U_n\)を有限個の開集合とするとき、共通部分\(\bigcap _{i=1} ^n U_i\)は開集合。
1.について。\(x \in \mathbb{R}^N\)を任意の点とすると、\(B(x,1) \subset \mathbb{R}^N\)は常に成り立つので、\(\mathbb{R}^N\)は開集合です。開球の半径は何でも良いですね。空集合については、その後の条件は常に真と考える(空真)ので、開集合です。開集合の候補となる点を内点と呼びますが、空集合ではその内点の集合が空集合であり、内点全体と一致しているので開集合とも言えます。
2.について。\((U_\lambda)_{\lambda \in \Lambda}\)を開集合族と仮定して、\(\bigcup _{\lambda \in \Lambda} U_\lambda\)が開集合であることを示しましょう。\(x \in \bigcup _{\lambda \in \Lambda} U_\lambda\)とすると、和集合の定義よりある\(\lambda \in \Lambda\)により\(x \in U_{\lambda}\)が成り立ちます。\(U_{\lambda}\)は開集合なので、ある開球が\(B(x, \varepsilon) \subset U_{\lambda}\)が成り立ちます。一般に、\(U_{\lambda} \subset \bigcup _{\lambda \in \Lambda} U_\lambda\)なので、\(B(x,\varepsilon) \subset \bigcup _{\lambda \in \Lambda} U_\lambda\)が成り立ち、開集合であることが言えました。
3.について。\(U_1,\dots, U_n\)を有限個の開集合とし、\(\bigcap _{i=1} ^n U_i\)が開集合であることを示します。\(x \in \bigcap _{i=1} ^n U_i\)とすると、すべての\(i=1,2,\dots,n\)について\(x \in U_{i}\)です。それぞれが開集合なので、\(B(x,\varepsilon_i)\subset U_{i}\)を満たす開球が存在します。その最小値として、\(\varepsilon := \min_{i\in \{1,\dots,n\}} \varepsilon _{i}\)としましょう。すると、すべての\(i\)に対して、\(B(x,\varepsilon) \subset U_{i}\)なので、\(B(x, \varepsilon) \subset \bigcap _{i=1} ^n U_i\)となり、開集合であることが言えました。
3.において有限性が必要な理由は、その証明を見ることでもわかります。無限個の開集合があると、その半径の正の最小値(下限)を見つけることは一般的にはできません。例えば\(\varepsilon_{i}= \frac{1}{n}\)となるような半径がそれぞれの開集合から見つかっても、\(n\to \infty \)でその半径は\(0\)になってしまい、開球を見つけられませんね。
閉集合についても、開集合と似たような性質が成り立ちます。
- \(\mathbb{R}^N\)、\(\varnothing \)は閉集合。
- \(V_1,\dots, V_n\)を有限個の閉集合とするとき、和集合\(\bigcup _{i=1} ^n V_i\)は閉集合。
- \((V_\lambda)_{\lambda \in \Lambda}\)を任意の閉集合族とするとき、共通部分\(\bigcap _{\lambda \in \Lambda} V_\lambda\)は閉集合。
一般に、任意の集合族\((A_{\lambda})_{\lambda \in \Lambda}\)に対して、ド・モルガンの法則が成り立ちます。全体集合を\(X\)として、
\[ \begin{aligned} X\backslash(\bigcup_{\lambda \in \Lambda} A_\lambda)= \bigcap_{\lambda \in \Lambda} (X \backslash A_\lambda)\end{aligned} \]
\[ \begin{aligned} X\backslash(\bigcap_{\lambda \in \Lambda} A_\lambda)= \bigcup_{\lambda \in \Lambda} (X \backslash A_\lambda)\end{aligned} \]
です。これは「任意の」と「ある」が否定の関係にあることから導かれるものです。
閉集合の性質は、ド・モルガンの法則を用いることで、開集合の性質に帰着して全て示せます(確かめてみてください)。
開集合の性質がそのまま閉集合の性質につながるように、開集合と閉集合は双対(そうつい dual)の関係にあると呼ばれます。表裏の関係にあることですね。
開集合は有限個の共通部分についてしか閉じていませんでしたが、閉集合ではそれが有限個の和集合についてしか閉じていない、ということに置き換わります。
例えば、\(\bigcup_{i \in \mathbb{N}} [0,1-\frac{1}{i}] =[0,1)\)です。\(1\)という点は、どんな自然数\(i\)を考えても、集合族に含まれません\(1 \not \in [0, 1- \frac{1}{i}]\) 。閉集合族の無限和ですが、右辺\([0,1)\)は閉集合ではありません(補集合において、\(1\)が内点ではない)。
今回紹介した開集合、閉集合の性質は、ユークリッド空間\(\mathbb{R}^N\)だけでなく、一般の距離空間\(X,d\)で全く同様に証明できます。実際、開球や開集合も距離さえあれば定義ができて、証明では特にユークリッド距離の性質を用いていません。
さらに一般に、距離を前提としない集合に対して「開集合」のような性質を持った空間を考えることができます。
\(X\)を一般の集合で、\(\mathcal{O}\)を\(X\)の部分集合からなる集合とする。
- \(X,\varnothing \in \mathcal{O}\)
- \((U_\lambda)_{\lambda \in \Lambda} \subset \mathcal{O}\)ならば、\(\bigcup _{\lambda \in \Lambda} U_\lambda \in \mathcal{O} \)
- \(U_1,\dots, U_n \in \mathcal{O}\)ならば、\(\bigcap _{i=1} ^n U_i \in \mathcal{O}\)
を満たす時、\( \mathcal{O}\)を\(X\)の開集合系、\( \mathcal{O}\)の要素を開集合と呼ぶ。
そして、組\((X, \mathcal{O})\)を位相空間(topological space)と呼ぶ。
距離空間で満たされていた開集合の「具体的な」性質を取り出して、その性質を満たすような一般的な集合たちを(新たに、一般の)「開集合」と呼ぶことにしよう、という考え方ですね。
このような抽象化は、ユークリッド空間から(抽象)ベクトル空間の定義を、ユークリッド内積・ノルム・距離から(抽象)内積・ノルム・距離空間の定義を取り出したのと、同様の議論です。具体的な状況で成り立っていた一般的な性質だけを取り出して、それを新たに定義として採用し、同様に考察できる対象を増やすのは、大学数学の常套手段であり、汎用性につながっています。
参考:ユークリッド空間R^Nの内積、ノルム、距離について解説、抽象ベクトル空間・線形空間の具体例R^N:順序対と直積集合
以上、ユークリッド空間における開集合、閉集合の性質を、具体例を挙げながら紹介してきました。
開集合系による位相空間の定義は、いきなり見るとどういうイメージを持てば良いのかわからないかもしれません。今回見てきたような、ユークリッド空間、距離空間における開集合・閉集合についてよく知っていれば、さらなる一般論も怖がらずに学ぶことができるでしょう。(位相空間論においては、ユークリッド空間や距離空間で通用した「常識」が、時には誤り・偏見になってしまうことに注意したいですが……。まずは具体的に知っていることを増やしていくのが大事だと思います。)
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (2018-11-06T00:00:00.000Z)
¥2,640
日本評論社 (2000-12-01T00:00:01Z)
¥2,420