どうも、木村(@kimu3_slime)です。
高校や大学の数学で、数列や級数といった内容を学びます。
何の役に立つのでしょうか? 今回はその例として、級数による数、関数の近似について簡単に紹介します。
数の近似
そもそも、一般的な数(実数)を小数(有理数)によって理解しようとすると、そこにはすぐに数列や級数による近似の発想が生まれてきます。
例えば、小数点以下に\(9\)がずっと続く数\(0.999\dots\)は、\(1\)に等しいです。
\[ \begin{aligned}0.999\dots =1\end{aligned} \]
無限に\(9\)が続くとは、どういう意味なのか曖昧です。
\(a_n := \frac{9}{10^n}\)により定まる数列\(\{a_n\}_{n\in \mathbb{N}}\)を考えましょう。\(a_1 =\frac{9}{10}=0.9\)、\(a_n = \frac{9}{100}= 0.09\)といった数が定まっています。
数列と言えば、各自然数\(n\)に対して値\(a_n\)が指定されたもの、無限数列を考えます。\(n\)をパラメータとして表に出すことで、「無限に続く」値がきちんと表現できているわけです。
そして、この数列により定まる有限和
\[ \begin{aligned}S_k := a_1 +a_2 +\cdots + a_k= \sum _{i=1} ^k \frac{9}{10^i}\end{aligned} \]
は、小数第\(k\)桁までに\(9\)が並んだ有理数を表します。その極限値として、
\[ \begin{aligned}0.999\dots := \lim _{k\to \infty} S_k\end{aligned} \]
と無限小数は定義されるわけです。ここで用いている有限和の極限は一般に、無限級数、あるいは単に級数と呼ばれます。
参考:「0.999…=1」はなぜ? 無限小数と数列の極限を解説
数の中には、繰り返しのある小数=有理数として表せないものがあります。それが無理数です。
無理数の例としては、\(\sqrt{2},\sqrt{3}\)を学校で学ぶでしょう。
\(\sqrt{2}\simeq 1.414\)
\(\sqrt{3}\simeq 1.732\)
といった値を覚えたかもしれません。これは近似値ですが、どうやって求めれば良いのでしょうか。
\(x^2 =2\)となる\(x\)が\(\sqrt {2}\)ですが、これをうまく近似する式が知られています。
\[ \begin{aligned}a_{n+1}=a_n+\frac{2-a_n ^2}{2a_n}\end{aligned} \]
\(a_1\)に適当な整数を代入し、この漸化式に従って計算していけば、その値は\(\sqrt {2}\)に限りなく近づいていきます。
この方法は、ニュートン法と呼ばれます。別記事で紹介予定。
参考:和算における開平法のルーツ―ギリシャから日本まで―堀 口 俊 二
関数の近似
微積分学や解析学において、級数論、収束半径などが論じられますが、その目的のひとつは、関数の近似があると思います。
有名な関数近似は、テイラー展開と呼ばれる多項式級数(べき級数)による近似です。
\[ \begin{aligned}\sin x=x- \frac{x^3}{3!}+ \frac{x^5}{5!}-\cdots\end{aligned} \]
\[ \begin{aligned}e^x = \sum_{n=0} ^{\infty} \frac{x^n}{n!}\end{aligned} \]
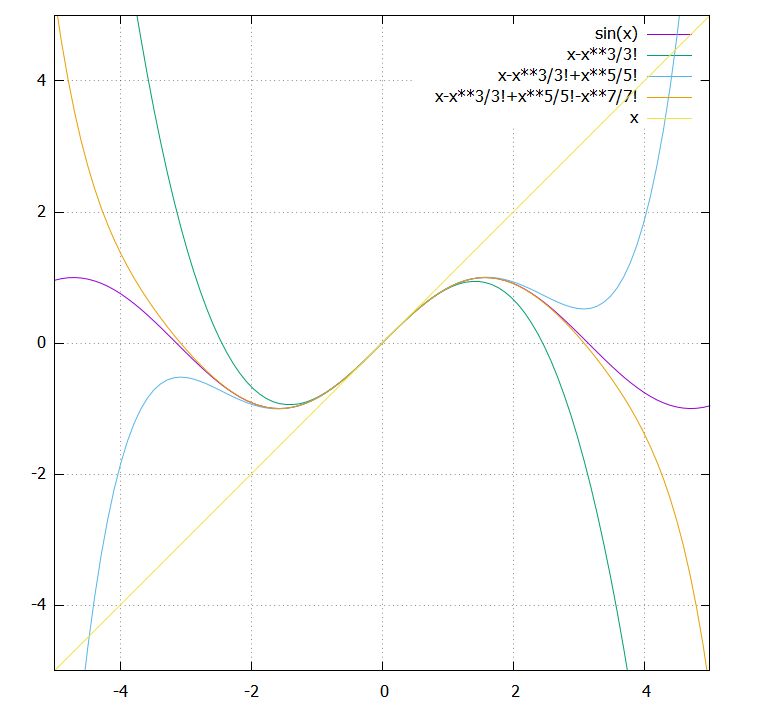
といった展開が成立します。関数\(f(x)\)を、\(x,x^2,x^3\)といった多項式を使った級数として展開できるのか、という話です。
適度に微分可能な関数は、
\[ \begin{aligned}f(x)=f(a)+f'(a)(x-a)+ \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n + R_{n+1}(x)\end{aligned} \]
と表せます。
この展開を無限に続けていったときに、その級数はきちんと元の関数を表すのかという問題は、級数の収束判定の話題につながります。
もうひとつ有名な関数の近似が、フーリエ級数展開です。今度は\(x^n\)といった多項式ではなく、\((\sin x)^n,(\cos x)^n\)といった三角関数を使った展開。
\[ \begin{aligned}f(x)= \begin{cases}0 & (-\pi <x <0 )\\1 & (0<x <\pi)\end{cases}\end{aligned} \]
\[ \begin{aligned}f(x)= \frac{1}{2} + \frac{2}{\pi} \sin x + \frac{2}{3\pi} \sin 3x + \frac{2}{5\pi} \sin 5x+ \cdots\end{aligned} \]
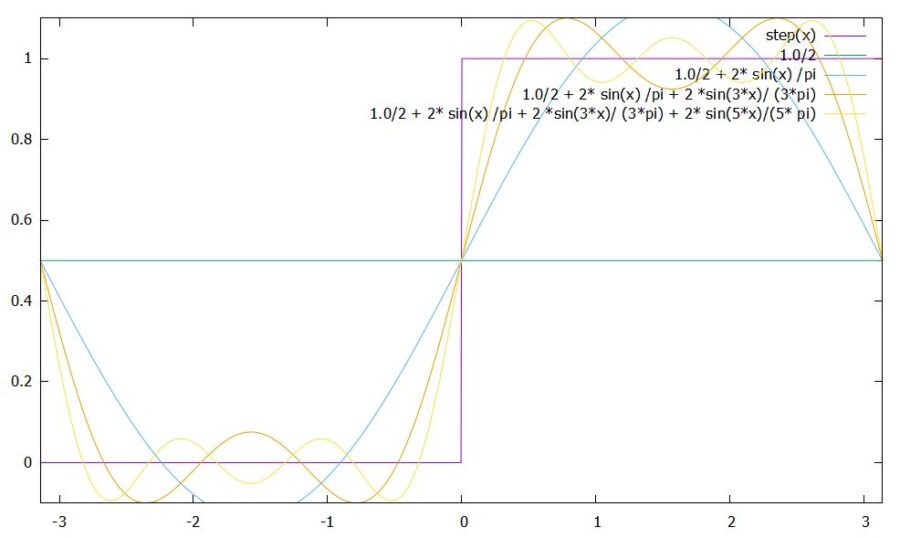
一般には、
\[ \begin{aligned} f(x)&=a_0 + a_1 \cos x + b_1 \sin x \\&+a_2 \cos 2x+ b_2 \sin 2x +\cdots \end{aligned} \]
といった展開が考えられます。
参考:線形代数の応用:関数の「空間・基底・内積」を使ったフーリエ級数展開
フーリエ級数の理論の応用として、
\[ \begin{aligned}\sum_{n=1}^{\infty}\frac{1}{n^2}\end{aligned} \]
といった級数の値(バーゼル問題)を求められます。パーセバルの等式については、別記事で紹介予定。
さらに一般化して、級数の値そのものを探求の対象としてみましょう。
\[ \begin{aligned}\zeta (z) :=\sum_{n=1}^\infty \frac{1}{n^z}\end{aligned} \]
は、リーマンのゼータ関数と呼ばれる関数です。不思議に思えるかもしれませんが、この関数は素数の個数を表す関数\(\pi(x)\)と関係しています。
この級数では、変数\(z\)を複素数の範囲にまで広げています。
複素数の世界まで考えると、1回でも微分できる関数(正則関数)はべき級数展開できるという強い性質があるのです。一方で、級数により定まる関数\(\sum_{n=0} ^{\infty} a_n z^n\)は、ただひとつの複素関数とつながっているのです(解析接続)。
複素級数を通して眺めれば、
\[ \begin{aligned}e^{i\theta} =\cos \theta + i \sin \theta\end{aligned} \]
というオイラーの公式も自然なものです。
実級数や実関数、実積分の背後には、複素関数や複素級数といった複素数の理論(複素解析)が隠れています。複素解析の準備としても、数列や級数が必要になってくるわけです。
今回は、数列や級数を学ぶ理由として、数や関数の近似について書きました。
無限に桁がありそうな数や、切れ目なくつながった関数を調べるには、それを近似する数列や級数を扱うのが有効です。
微積分や解析学での学びを通じて、ぜひ近似という発想と使い方を身に着けてみてください。
木村すらいむ(@kimu3_slime)でした。ではでは。
岩波書店 (1978-03-23T00:00:01Z)
¥5,170
東京大学出版会 (1980-03-31T00:00:01Z)
¥3,080
こちらもおすすめ
lim 1/n=0はなぜ? ε-n_0論法とアルキメデスの性質
漸化式(フィボナッチ数列)を線形代数(線形空間、固有ベクトル)で解く方法を解説


